绕单轴的旋转矩阵

标签：初始   form   坐标   表示   box   坐标转换   就是   法则   顺序   

对于绕单轴的旋转矩阵，很多小伙伴分不清楚到底是B转W还是W转B的，下面就先用上面对旋转矩阵的理解来推导一下绕单轴的旋转矩阵，然后介绍下怎么记忆。注意对旋转正负号的定义，惯用的定义是，从原点沿着坐标轴看，顺时针为正。下面看图。

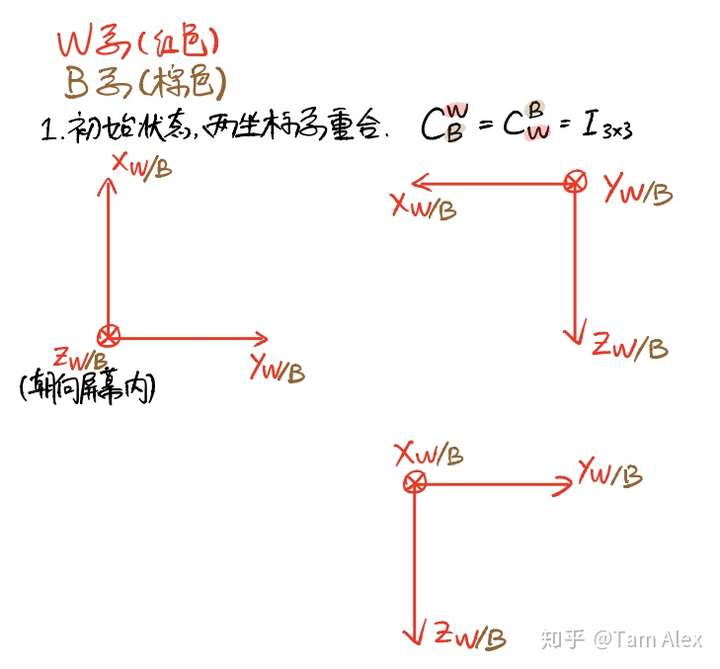初始状态的W和B系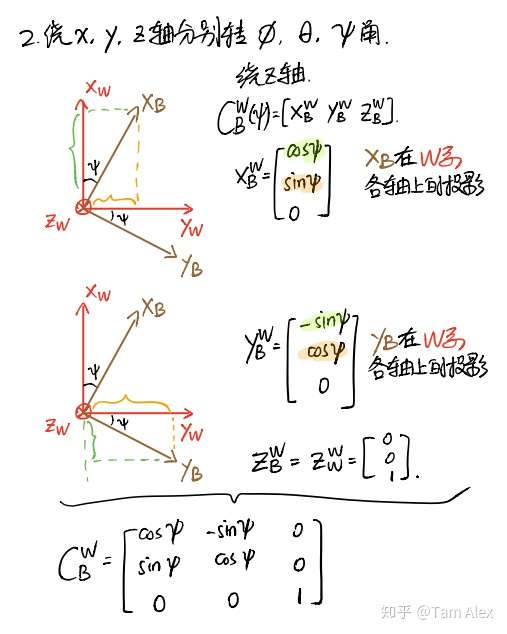绕Z轴旋转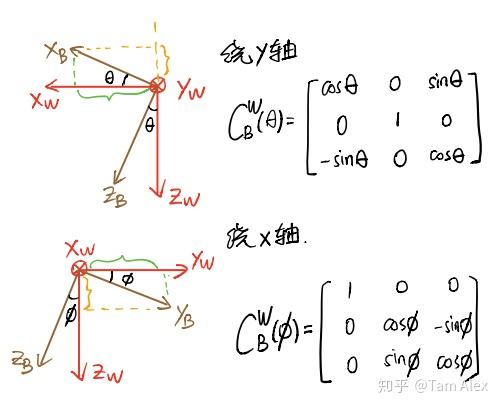绕Y、X轴旋转

这样就通过计算B系各坐标轴在W系的投影得到了绕各轴旋转的  ，反之计算W系在B系的投影就可得到绕各轴旋转的  ，不过因为它们互为转置，所以得到了一个，就知道另一个了。

注意这里的W系和B系可以换成任意两个坐标系，只要把握哪个坐标系是动坐标系，以及我们要找哪个坐标系到哪个坐标系的旋转矩阵就不容易出错了。

绕单轴的旋转矩阵对角线都是余弦或1，其他的0元素也很容易确定，讨厌的就是正弦函数前面的正负号了。那么我的记忆方法就是。。。还是把旋转的两个轴画出来，然后只要确定一个正弦的符号，另一个位置的正弦取相反的符号就行了。确实还是挺麻烦，不过按照这个理解是不会搞错B转W和W转B的，大家可以试一试。

我们把绕x、y、z的从B系到W系的单轴旋转矩阵分别  、  、  ，那么就有  ，正好对应了从B系到W系的旋转顺序。这也叫链式法则，相信大家看过相关书都明白，以及旋转矩阵的逆就是它的转置，表示相反的坐标转换，也都不再赘述。

绕单轴的旋转矩阵

标签：初始   form   坐标   表示   box   坐标转换   就是   法则   顺序   

原文地址：https://www.cnblogs.com/yibeimingyue/p/12069347.html