标签：元素   numbers   访问   有序   第一个   image   函数   python   not   

1. 查找算法

描述顺序查找与二分法（折半搜索）的概念以及用python实现其查找流程

一、顺序查找

1. 什么是顺序查找

当数据存储在诸如列表的集合中时，我们说这些数据具有线性或顺序关系。 每个数据元素都存储在相对于其他数据元素的位置。 由于这些索引值是有序的，我们可以按顺序访问它们。 这个过程产实现的搜索即为顺序查找。

2. 顺序查找原理剖析：

从列表中的第一个元素开始，我们按照基本的顺序排序，简单地从一个元素移动到另一个元素，直到找到我们正在寻找的元素或遍历完整个列表。如果我们遍历完整个列表，则说明正在搜索的元素不存在。

3. 代码实现

该函数需要一个列表和我们正在寻找的元素作为参数，并返回一个是否存在的布尔值。found 布尔变量初始化为 False，如果我们发现列表中的元素，则赋值为 True。

# 最常见的就是for遍历列表的顺序查找算法
# 时间复杂度O(n)
#Question: Given a sorted list of numbers, find the index of a specific value in the list. If no such value, return -1.

def sequential_search(lis, key):
    for i in range(len(lis)):
        if lis[i] == key:
            return i
    else:               #注意else的缩进位置，与if并列的话都会返回False
        return False

alist = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222] 
result = sequential_search(alist, 123)
print(result)

#输出结果
3

二、二分查找

1. 算法原理

在查找表中不断取中间元素与查找值进行比较，以二分之一的倍率进行表范围的缩小。
查找表类型：有序表查找，查找表中的数据必须按某个主键进行某种排序。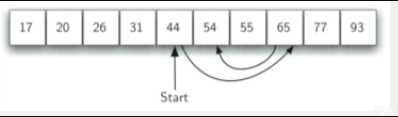

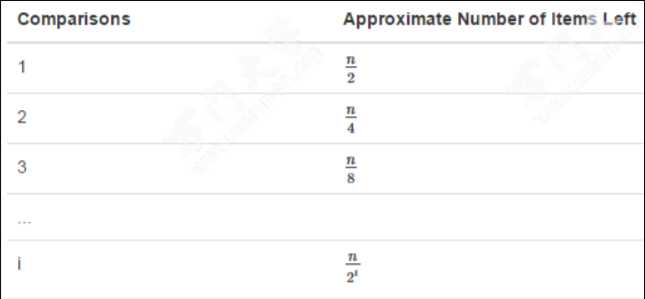
2. 算法分析

由此可得算法时间复杂度为O(logn)，比O(n)更优

3.代码实现

def middle(alist,item):
    if len(alist) == 0:           #判断边界条件
        return -1
    #列表的起始点和终点
    find = False
    low = 0
    high = len(alist)-1
    
    while not find and low <= high:
        mid = (low+high)//2 #中间元素下标
        #插好的值大于了中间元素的值，意味着查找的值只可能出现在中间元素的右侧
        if item > alist[mid]:
            low = mid + 1
        elif item == alist[mid]:#查找的值和中间元素值相等，意味着找到了
            find = True
        else:#查找的值小于中间元素，意味着查找的值只可能出现中间元素的左侧
            high = mid - 1
    return find

alist = [1,2,3,4,5,6,7]
print(middle(alist,7))
# 输出结果
True

三、哈希查找

待补充

6. 常用排序算法

列表查找及二分查找

标签：元素   numbers   访问   有序   第一个   image   函数   python   not   

原文地址：https://www.cnblogs.com/zhangdadayou/p/12070553.html