标签:fine ack 技术 targe 初始 tmp log return 价值
复现链接:https://ac.nowcoder.com/acm/contest/3405#question
shzr题解:https://www.cnblogs.com/shzr/p/12018915.html
echozhou题解:https://www.cnblogs.com/EchoZQN/p/12030689.html
输入3输出10,输入5输出16,盲猜一发3n+1,看了第三个样例输入9输出10,陷入沉思。
开始推断发现n+1进制符合,理由如下:
假设为n+1进制的cba,转换为十进制后为下式
(n+1)*a+(n+1)*(n+1)*b+(n+1)*(n+1)*(n+1)*c
mod的性质:(a*b*c)%n=[(a%n)*(b%n)*(c%n)]%n
而(n+1)%n=1,故原式%n=1*a+1*1*b+1*1*1+c=a+b+c
任意n+1进制的数同理,1+kn(k>=1)进制的数同理,因为(1+kn)%n=1
要注意如果输出不是n+1,需要开long long,因为n的范围是1e9
#include<bits/stdc++.h> using namespace std; int main() { int n; scanf("%d",&n); printf("%d\n",n+1); return 0; }
dp[i]表示i节点向子树内能延伸的最长路径
dep[i]表示i节点到k节点的距离,初始假定dep[k]=1
dfs记录深度
redfs逆dp,输出路径
样例:
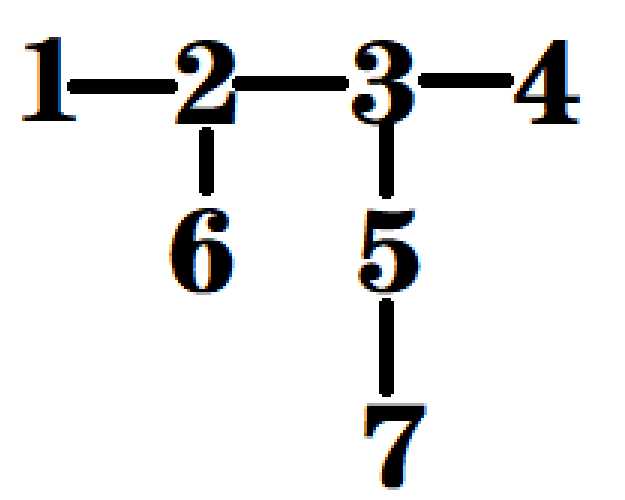
#include<bits/stdc++.h> using namespace std; #define inf 0x3f3f3f3f const int maxn=1e5+10; vector<int> vec[maxn]; int dp[maxn],dep[maxn]; void dfs(int x) { int size=vec[x].size(); for(int i=0;i<size;i++) { int tmp=vec[x][i]; if(dep[tmp])continue;//不能只当作vis来判断是否出现过,下面要用到dep dep[tmp]=dep[x]+1; dfs(tmp); dp[x]=max(dp[x],dp[tmp]); } dp[x]++;//加上x点本身 } void redfs(int x) { printf("%d\n",x); if(dp[x]==1)return; int size=vec[x].size(),ans=inf; for(int i=0;i<size;i++) { int tmp=vec[x][i]; if(dep[tmp]<dep[x])continue; if(dp[tmp]+1==dp[x])ans=min(ans,tmp);//优先选择节点最小的 } redfs(ans); } int main() { int n,k; scanf("%d%d",&n,&k); for(int i=0;i<n-1;i++) { int u,v; scanf("%d%d",&u,&v); vec[u].push_back(v); vec[v].push_back(u); } dep[k]=1; dfs(k); redfs(k); /* for(int i=1;i<=n;i++) { cout<<i<<" "<<dp[i]<<" "<<dep[i]<<endl; }*/ return 0; }
代码很简单但是我想了很久
范围n<=200,V、v[i]<=1e6,w[i]<=200
题意:总体积不小于V的最小价值
转换:总体积不大于Vall-V的最大价值(开不了这么大的数组)
再次转换:对价值进行dp,dp[i]表示同价值最大体积,从价值1到最大价值,存在不小于V体积dp[i],此时的价值i即为答案
#include<bits/stdc++.h> using namespace std; const int maxv=1e6+10; const int maxw=200+10; int v[maxw],w[maxw],dp[maxv];//dp[i]表示价值是i的情况下的最大体积 int main() { int n,V,sum=0; scanf("%d%d",&n,&V); for(int i=1;i<=n;i++) { scanf("%d%d",&v[i],&w[i]); sum+=w[i]; } for(int i=1;i<=n;i++) { for(int j=sum;j>=w[i];j--) { dp[j]=max(dp[j],dp[j-w[i]]+v[i]); } } //找到第一个满足体积不小于V的价值 for(int i=1;i<=sum;i++) { if(dp[i]>=V) { printf("%d\n",i); break; } } return 0; }
单调队列giao一下
加入了自己领悟的代码
#include<bits/stdc++.h> using namespace std; const int maxn=1e5+10; pair<int,int> a[maxn]; struct cmp { bool operator()(int a,int b) { return a>b; } }; int main() { int n,p; long long ans[maxn]={0}; scanf("%d%d",&n,&p); for(int i=1;i<=n;i++) { scanf("%d",&a[i].first); a[i].second=i; } sort(a+1,a+n+1); priority_queue<int,vector<int>,cmp> q;//id小的优先 //priority_queue<int,vector<int>,greater<int> > q; long long cur=0; for(int i=1;i<=n;i++)//保证Push n个数 { while(!q.empty()&&cur<a[i].first)//如果打水队列不空,而且还没轮到a[i]打水(a[i]已经为升序) { int id=q.top();//就不停地让队列里第一个人去打水 q.pop(); //cout<<id<<" "<<cur<<" "<<a[i].first<<endl; cur+=p; ans[id]=cur; } q.push(a[i].second);//a[i]排队 if(cur<a[i].first)cur=a[i].first; //如果a[i]前面的人都打过水了,cur还没轮到a[i],cur之间变成a[i]的时间 } //for一遍后n个人肯定都已经排过队了,把还没打水的排一遍队 while(!q.empty()) { int id=q.top(); q.pop(); cur+=p; ans[id]=cur; } for(int i=1;i<=n;i++) { cout<<ans[i]<<" "; } return 0; }
在树上找两条不相同的路径,使得两路径的交最长
树上最长的路径为直径,该路径少取一个节点后产生的新路径,与直径相交,长度刚好为n-1
为啥不是n?
反证法:假设答案为n(直径),即树上存在两条不相同的路径,他们的交为n,因为两条路不同,所以肯定有至少一条路在除了交的部分还有边,那树上最长的路就大于n了,与原假设矛盾。
故答案不为n。
剩下就是怎么求树的直径了...
不学不知道,树形dp原来so easy?:)
#include<bits/stdc++.h> using namespace std; const int maxn=2e5+10; vector<int> vec[maxn]; int vis[maxn],dp[maxn],ans; //dp[i]为以i为起点的最长链的长度 void dfs(int u) { vis[u]=1; int size=vec[u].size(); for(int i=0;i<size;i++) { int now=vec[u][i]; if(vis[now])continue; dfs(now); //cout<<u<<" "<<now<<endl; ans=max(ans,dp[u]+dp[now]+1); //在u为根节点时,经过u的最长链长度等于它的任意两个子节点的d[i]之和的最大值+1 //每个u都会遍历一遍,所以可以求出ans dp[u]=max(dp[u],dp[now]+1); } } int main() { int n; scanf("%d",&n); for(int i=0;i<n-1;i++) { int u,v; scanf("%d%d",&u,&v); vec[u].push_back(v); vec[v].push_back(u); } dfs(1); cout<<ans-1<<endl; return 0; } /* 7 1 2 2 6 2 3 3 4 3 5 5 7 */
先mark,有空了滚回来补题
标签:fine ack 技术 targe 初始 tmp log return 价值
原文地址:https://www.cnblogs.com/myrtle/p/12070920.html