扩展KMP

标签：turn   lin   ++   png   code   inline   方法   处理   tga   

这个算法主要靠画图理解，于是学习的时候画了不少图，正好写篇博客。

扩展KMP能解决的问题：
给定两个串\(S,T\)，对于S的每一个后缀\(S[i...n]\)求和\(T\)的\(LCP\)。

设\(exnxt_i\)表示后缀\(S[i...n]\)求和\(T\)的\(LCP\)，我们要做的就是求所有\(exnxt_i\)。

我们先对\(T\)处理出\(nxt_i\)表示\(T\)的后缀\(T[i...m]\)和\(T\)的\(LCP\)，如何处理之后再说。

1.如何求\(exnxt\)：

假设我们已经求出了\([1,i-1]\)的\(exnxt\)，我们现在要求\(exnxt_i\)。

我们维护\(p\)表示对于\([1,i-1]\)它们在\(S\)上最远和\(T\)匹配到了哪里，用式子说就是\(max_{j\in [1,i-1]}(j+extnxt_j-1)\)，并且我们维护这是在哪个点取到的，记为\(p0\)。

先上一张图：

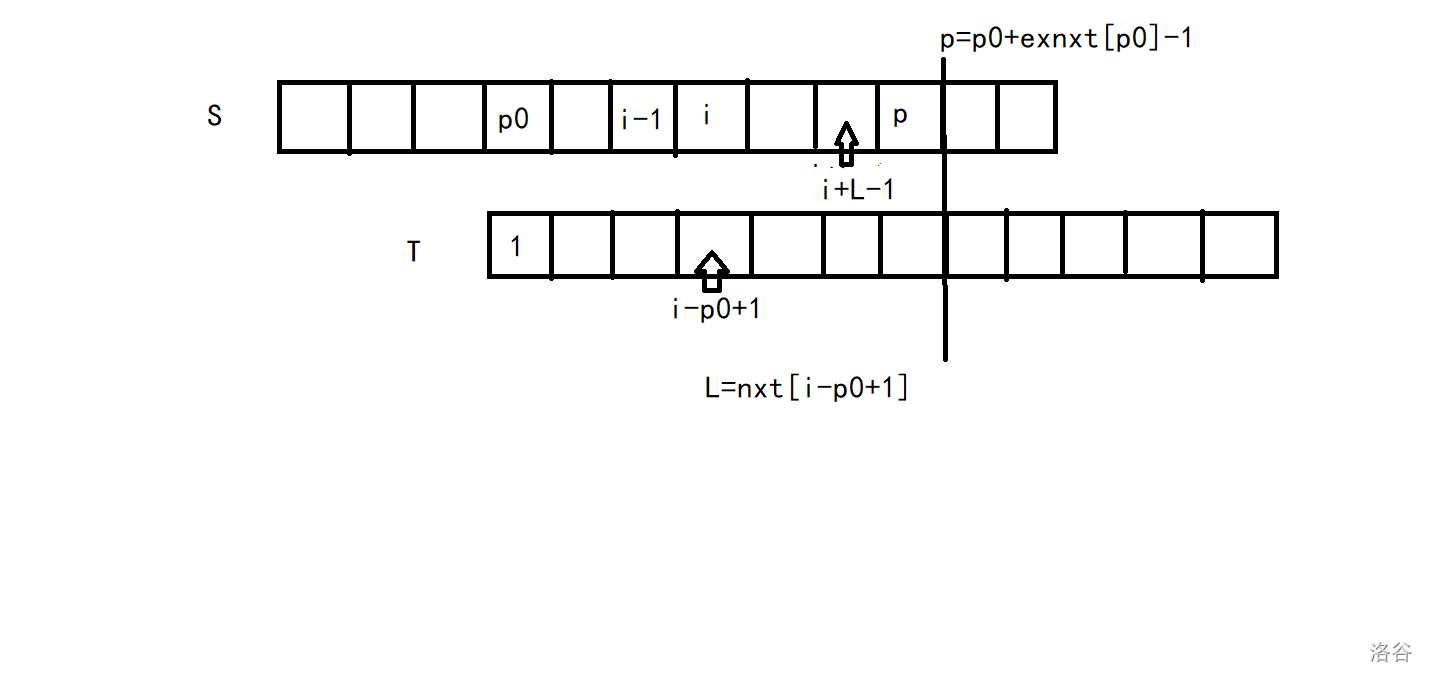
我们现在是在\(p0\)匹配好的时候，我们观察\(i\)的位置，不难发现\(i\)此时对应着\(i-p0+1\)。

我们设\(L=nxt_{i-p0+1}\)，那么根据已知信息，即\(nxt\)的定义，我们能知道：
\(T[1...L]=T[i+p0-1...(i+p0-1)+L-1]=S[i...i+L-1]\)

即下图三线相等：

这时如果\(i+L-1<p\)（注意不能取等，我们并不知道\(p\)之后的信息），那么我们实际已经求完了，此时\(exnxt_i=L\)。

代码非常简单（代码中\(r\)即为\(p\)）：

if(i+nxt[i-p0+1]-1<r)exnxt[i]=nxt[i-p0+1];

接下来考虑如果\(i+L-1\geqslant p\)会怎样：

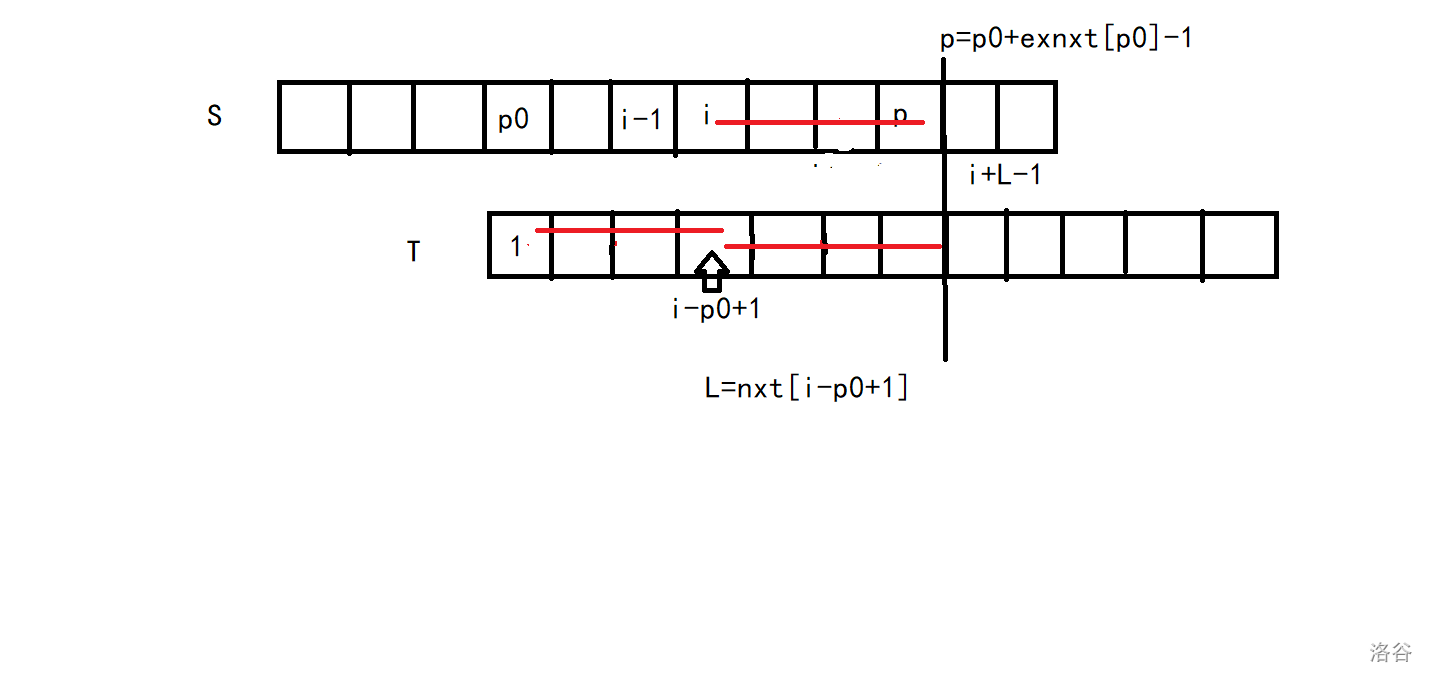
这时我们只能知道如下三条线是相等的，即：
\(T[1...p-i+1]=T[i-p0+1...(i-p0+1)+(p-i+1)-1]=S[i...i+(p-i+1)-1]\)

于是我们让\(extnxt_i\)先有一个候选答案\(p-i+1\)之后，我们暴力匹配，不断扩展\(extnxt_i\)。

代码是这样的（代码中的\(r\)就是\(p\)）：

exnxt[i]=max(r-i+1,0);
while(s[i+exnxt[i]]==t[exnxt[i]+1])exnxt[i]++;

之后我们让\(p0=i\)，更新\(p\)的值（代码中的\(r\)就是\(p\)）：

p0=i,r=i+exnxt[i]-1;

感性理解的话因为\(p\)的增长是\(O(n)\)的，所以整个算法的复杂度是\(O(n)\)的。

2.如何求\(nxt\)：

我们发现\(nxt\)的定义和\(exnxt\)的定义十分相像，不过一个是\(T\)和\(T\)匹配，一个是\(S\)和\(T\)匹配。

于是我们用同样的方法就可以求出\(nxt\)：暴力算出\(nxt_1,nxt_2\)，之后按照1.中的方法求即可。

模板题

说来我好像是题解中第二个从1开始数数的。。。不过扶苏的代码太神仙了，我看不懂。

code:

#include<bits/stdc++.h>
using namespace std;
const int maxn=100010;
int n,m;
int nxt[maxn],exnxt[maxn];
char s[maxn],t[maxn];
inline void getnxt()
{
    nxt[1]=m;nxt[2]=0;
    while(t[1+nxt[2]]==t[2+nxt[2]])nxt[2]++;
    for(int i=3,p0=2,r=p0+nxt[p0]-1;i<=m;i++)
    {
        if(i+nxt[i-p0+1]-1<r)nxt[i]=nxt[i-p0+1];
        else 
        {
            nxt[i]=max(r-i+1,0);
            while(t[nxt[i]+1]==t[i+nxt[i]])nxt[i]++;
            p0=i,r=i+nxt[i]-1;
        }
    }
}
inline void getexnxt()
{
    exnxt[1]=0;
    while(s[1+exnxt[1]]==t[1+exnxt[1]])exnxt[1]++;
    for(int i=2,p0=1,r=p0+exnxt[p0]-1;i<=n;i++)
    {
        if(i+nxt[i-p0+1]-1<r)exnxt[i]=nxt[i-p0+1];
        else 
        {
            exnxt[i]=max(r-i+1,0);
            while(s[i+exnxt[i]]==t[exnxt[i]+1])exnxt[i]++;
            p0=i,r=i+exnxt[i]-1;
        }
    }
}
int main()
{
    //freopen("test.in","r",stdin);
    //freopen("test.out","w",stdout); 
    scanf("%s%s",s+1,t+1);
    n=strlen(s+1);m=strlen(t+1);
    getnxt();getexnxt();
    for(int i=1;i<=m;i++)printf("%d ",nxt[i]);
    puts("");
    for(int i=1;i<=n;i++)printf("%d ",exnxt[i]);
    return 0;
}

扩展KMP

标签：turn   lin   ++   png   code   inline   方法   处理   tga   

原文地址：https://www.cnblogs.com/nofind/p/12074323.html