标签:概率 特定 com -- get 曲线 crete 概率论 通过
概率(Probability):事件发生的可能性的数值度量。
组合(Combination):从n项中选取r项的组合数,不考虑排列顺序。组合计数法则: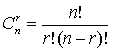 。
。
排列(Permutation):从n项中选取r项的组合数,考虑排列顺序。排列计数法则: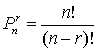 。
。
贝叶斯定理(Bayes‘s Theorem):获取新信息后对概率进行修正的一种方法。先验概率--->新信息--->应用贝叶斯定理--->后验概率。具体请见:贝叶斯定理推导(Bayes‘s Theorem)。
离散型概率分布(Discrete Probability Distribution):伯努利分布,二项分布,泊松分布,几何分布,超几何分布,多项分布
连续型概率分布(Continous Probability Distribution):指数分布,正态分布,均匀分布
抽样概率分布(Sampling Probability Distribution):t分布,卡方分布,F分布
常见的概率分布类型(一)(Probability Distribution I)
常见的概率分布类型(二)(Probability Distribution II)
概率质量函数 (Probability Mass Function,pmf):离散随机变量在各特定取值上的概率。
概率密度函数(Probability Density Function,pdf):连续随机变量在一定区间内取值的概率, 不直接给出概率值,曲线下的面积才是概率,需要通过对这段区间进行积分来求。
(注:曲线下单个点的面积为0,所以连续随机变量取某一特定值的概率是0。)
累积分布函数(Cumulative Distribution Function,CDF):对于离散分布,cdf可以通过定义得到,而其函数形状应该是阶梯状的;对连续函数,是所有小于等于a的值出现概率的和,即F(a)=P(x<=a),可以通过对概率密度函数积分得到。
标签:概率 特定 com -- get 曲线 crete 概率论 通过
原文地址:https://www.cnblogs.com/HuZihu/p/11942127.html