标签:for tco lse text img ret 图片 mic family
该题目为求解三维形体的表面积,主要是求解过程很清晰,数学问题!
题目描述:
在 N * N 的网格上,我们放置一些 1 * 1 * 1 的立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
请你返回最终形体的表面积。
实例1
输入:[[2]] 输出:10
实例2
输入:[[1,2],[3,4]] 输出:34
分析:
实例1可知,当只有一摞立方体时,其表面积可以直接由长方体面积公式求得,S=grid[i][j]*4+2,四个侧面积加上下底面积即可!
实例2:
相邻的两个立方体会进行吸收,因此,相邻的表面积应该是较高的部分,减去较低的部分的剩余面积,我们需要进行分层计算。
对于这个实例,分析如下:
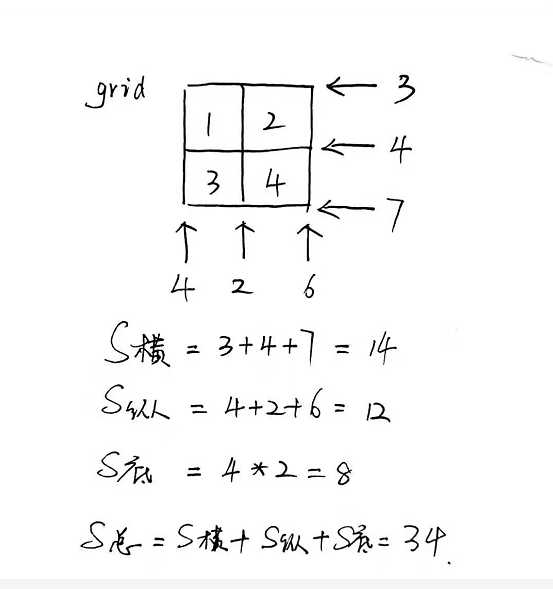
S横:以行为单位,第一行和最后一行的面积直接相加,其余相邻部分由相邻方块的差的绝对值构成;
S纵:以列为单位,第一列和最后一列的面积直接相加,其余相邻部分同样由相邻方块差的绝对值构成;
S底:只要单元格内有方块,就加上、下两个底面积,S底+=2,(不管是几个)
总面积则等于三块面积相加总和,代码如下:
1 class Solution { 2 public: 3 int surfaceArea(vector<vector<int>>& grid) { 4 if(grid.size()==1) 5 return grid[0][0]*4+2; 6 int N=grid.size(); 7 int count=0; 8 //先计算横向面积 9 for(int i=0;i<N;i++) 10 { 11 for(int j=0;j<N;j++) 12 { 13 if(i==0) //首行相加 14 count+=grid[i][j]; 15 else{ 16 count+=abs(grid[i][j]-grid[i-1][j]); //其余等于差的绝对值 17 } 18 if(i==N-1) //尾行直接相加 19 count+=grid[i][j]; 20 } 21 } 22 //cout<<"hengxiang is "<<count<<endl; 23 //再计算纵向面积 24 for(int j=0;j<N;j++) 25 { 26 for(int i=0;i<N;i++) 27 { 28 if(j==0) //首列直接相加 29 count+=grid[i][j]; 30 else{ 31 count+=abs(grid[i][j]-grid[i][j-1]); //其余等于差的绝对值 32 } 33 if(j==N-1) //尾列直接相加 34 count+=grid[i][j]; 35 } 36 } 37 //计算上下面积 38 int sum=0; 39 for(int i=0;i<N;i++) 40 { 41 for(int j=0;j<N;j++) 42 { 43 if(grid[i][j]>0) 44 sum++; 45 } 46 } 47 //cout<<"sum is "<<sum<<endl; 48 count+=(sum*2); //上下两个底面积,加到结果上 49 50 return count; 51 } 52 };
简单题而已,清晰的编程思路很重要~~~
标签:for tco lse text img ret 图片 mic family
原文地址:https://www.cnblogs.com/cnyulei/p/12077454.html