标签:其他 举例 方法 模拟 基础 max 通过 左右 heap
刚开始学treap。。同学在台上给我们讲,貌似除我之外的机房dalao们都听懂了就我发呆。。。(滑稽)
于是,事后的窝只能自己上网翻书研究了。。。。
treap:
treap=tree+heap,树+堆
也就是说,这个东西是个树,但是满足堆的性质。
前置知识:
BST二叉搜索树:
度娘曰:
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
也就是说,你把它从根节点中序遍历一边就能得到一个从小到大的数列。
大概长这样子:
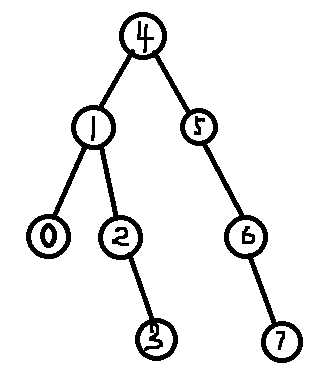
对于4:左边子树节点的权值为0 1 2 3,都比4小,右边子树节点的权值为5 6 7,都比4大。
对于1:左边子树节点权值为0,比1小,右边子树节点权值为2 3,比1大(且比4小)。
对于其他节点同理。
一个不难理解的东西。
堆:
priority_queue。。。
堆中某个节点的值总是不大于或不小于其父节点的值;
这里就不再手写堆了,‘’
回过头来:
根据BST的定义我们可以知道,任意选取一个数做为根节点,在整个数列中一定能找到比他小的数和比他大的数(或者其中一个不存在),同样的,对于它的子树也是根节点不确定的。
有些毒瘤! 出题人会拿duliu数据把BST卡成一条链,然后多次询问,复杂度直接爆炸。
那么为了均摊一下BST的深度,使得每次询问时间复杂度都接近logn的话,我们需要对它进行一系列操作:
赋权值:
我们随机为每一个节点赋值一个权值pri,对于pri我们要求pri低的深度小,也就是小根堆的性质,因为rand每次都随机的话是可以均摊一下节点的深度(具体的原理我还一时半会说不清。。感性李姐)
如何调整节点使得其满足堆序:
在节点插入时,和bst一样建立,找到自己节点应该在的位置,当当前节点为空时,建立新节点,rand它的pri后返回,对其进行左右旋转操作。
左旋:就是把根节点转移到其左子节点的位置,并维护BST。
方法:直接上图:
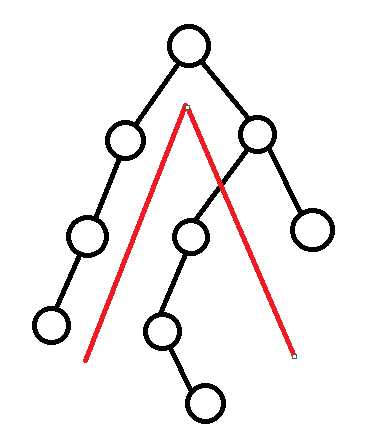
我们可以按照红线的方法来划分子树;
这样就是上面的一条链和下面的又子节点的子树两部分了。
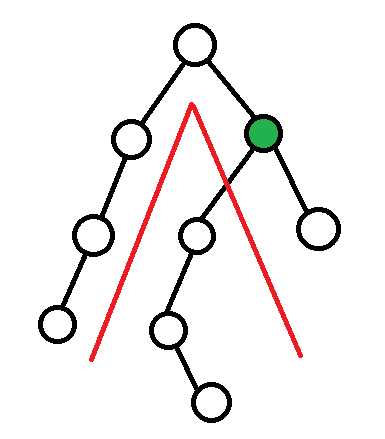
旋转后,绿色节点到达根节点位置,也就是把整条链往左拽了一下;子树换了父亲,认左边的节点为爸爸了:
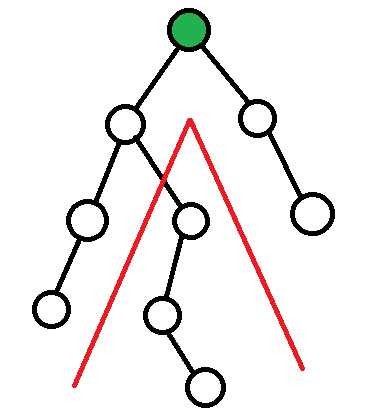
就这样完了。
右旋:换个方向搞左旋。
删除节点:
删除时,如果该节点对应size>1,则size--,否则将其权值pri赋为inf或者清空。之后我们可以通过比较左右子树pri的大小决定谁做新的根(为了满足堆的性质,单数不管是左子树根节点还是右子树根节点做新的根,都不会影响BST性质,感性模拟),之后根节点就变成了原来左子树/右子树中的一员,继续递归下去,直到成为叶节点,也就是这一段开头说的那句话的情况。之后我们就可以直接删除它了。
求前驱后继:
一个数x的前驱定义为小于这个数的最大的数。后继就是大于等于这个数的最小的数。
理解如何递归:
以前驱举例子,因为要找小于这个数的最大的数,那么肯定到左子树去找;
如果当前节点大于等于根节点的值,到左子树里面找;
如果当前节点空的,返回inf,
else,如果当前节点的val<x 则返回max(v,去右子树递归的返回值);
else,说明答案还在左子树里面,那么就到左子树去找。
原理基本讲解完毕。
学会的人去切:https://www.luogu.com.cn/problem/P3369
完结、
标签:其他 举例 方法 模拟 基础 max 通过 左右 heap
原文地址:https://www.cnblogs.com/lbssxz/p/12046014.html