标签:efi 图片 模式匹配 存储方式 build 关于 后缀数组 程序 lambda
串的主分支-字符串
字符串主要用于编程,概念说明、函数解释、用法详述见正文,
这里补充一点:字符串在存储上类似字符数组,所以它每一位的单个元素都是可以提取的,
如s=“abcdefghij”,则s[1]=“b”,s[9]="j",而字符串的零位正是它的长度,如s[0]=10,
这可以给我们提供很多方便,如高精度运算时每一位都可以转化为数字存入数组。
中文名 字符串
外文名 Character string
拼 音 zi fu chuan
简 称 串(String)
记 作 s=“a1a2···an”(n>=0)
释 义 编程语言中表示文本的数据类型
简介
字符串或串(String)是由数字、字母、下划线组成的一串字符。一般记为 s=“a1a2···an”(n>=0)。它是编程语言中表示文本的数据类型。在程序设计中,字符串(string)为符号或数值的一个连续序列,如符号串(一串字符)或二进制数字串(一串二进制数字)。
通常以串的整体作为操作对象,如:在串中查找某个子串、求取一个子串、在串的某个位置上插入一个子串以及删除一个子串等。两个字符串相等的充要条件是:长度相等,并且各个对应位置上的字符都相等。设p、q是两个串,求q在p中首次出现的位置的运算叫做模式匹配。串的两种最基本的存储方式是顺序存储方式和链接存储方式。
设 Σ 是叫做字母表的非空有限集合。Σ 的元素叫做“符号”或“字符”。在 Σ 上的字符串(或字)是来自 Σ 的任何有限序列。例如,如果 Σ = {0, 1},则 0101 是在 Σ 之上的字符串。
字符串的长度是在字符串中字符的数目(序列的长度),它可以是任何非负整数。“空串”是在 Σ 上的唯一的长度为 0 的字符串,并被指示为 ε 或 λ。
在 Σ 上的所有长度为 n 的字符串的集合指示为 Σn。例如,如果 Σ = {0, 1} 则 Σ2 = {00, 01, 10, 11}。注意 Σ0 = {ε} 对于任何字母表 Σ。
在 Σ 上的所有任何长度的字符串的集合是 Σ 的Kleene闭包并被指示为 Σ*。 依据Σn, 。例如,如果 Σ = {0, 1} 则 Σ* = {ε, 0, 1, 00, 01, 10, 11, 000, 001, 010, 011, …}。尽管 Σ* 自身是可数无限的,Σ* 的所有元素都有有限长度。
在 Σ 上一个字符串的集合(就是 Σ* 的任何子集)被称为在 Σ 上的形式语言。例如,如果 Σ = {0, 1},则带有偶数个零的字符串的集合({ε, 1, 00, 11, 001, 010, 100, 111, 0000, 0011, 0101, 0110, 1001, 1010, 1100, 1111, …})是在 Σ 上的形式语言。
字符编码
历史上,字符串数据类型为每个字符分配一个字节,尽管精确的字符集随着区域而改变,字符编码足够类似得程序员可以忽略它
— 同一个系统在不同的区域中使用的字符集组要么让一个字符在同样位置,要么根本就没有它。这些字符集典型的基于ASCII码
或EBCDIC码。
意音文本的语言比如汉语、日语和朝鲜语(合称为CJK)的合理表示需要多于256个字符(每字符一个字节编码的极限)。常规的解决
涉及保持对ASCII码的单字节表示并使用双字节来表示CJK字形。现存代码在用到它们会导致一些字符串匹配和切断上的问题,严
重程度依赖于字符编码是如何设计的。某些编码比如EUC家族保证在ASCII码范围内的字节值只表示ASCII字符,使得使用这些字
符作为字段分隔符的系统得到编码安全。其他编码如ISO-2022和Shift-JIS不做这种担保,使得基于字节的代码做的匹配不安全。
另一个问题是如果一个字符串的开头被删除了,对解码器的重要指示或关于在多字节序列中的位置的信息可能就丢失了。另一个
问题是如果字符串被连接到一起(特别是在被不知道这个编码的代码截断了它们的结尾之后),第一个字符串可能不能导致编码器
进入适合处理第二个字符串的状态中。
Unicode也有些复杂的问题。多数语言有Unicode字符串数据类型(通常是UTF-16,因为它在Unicode补充位面介入之前就被增
加了)。在Unicode和本地编码之间转换要求理解本地编码,这对于现存系统要一起传输各种编码的字符串而又没有实际标记出它
们用了什么编码就是个问题。
主要操作
1. 连接运算 concat(s1,s2,s3…sn) 相当于s1+s2+s3+…+sn.
例:concat(‘11’,‘aa’)=‘11aa’;
2. 求子串 Copy(s,I,I) 从字符串s中截取第I个字符开始后的长度为l的子串。
例:copy(‘abdag’,2,3)=’bda’
3. 删除子串 过程 Delete(s,I,l) 从字符串s中删除第I个字符开始后的长度为l的子串。
例:s:=’abcde’;delete(s,2,3);结果s:=’ae’
4. 插入子串 过程Insert(s1,s2,I) 把s1插入到s2的第I个位置
例:s:=abc;insert(‘12’,s,2);结果s:=’a12bc’
5. 求字符串长度 length(s) 例:length(‘12abc’)=5
在ASP中 求字符串长度用 len(s)例: len("abc12")=5
6. 搜索子串的位置 pos(s1,s2) 如果s1是s2的子串 ,则返回s1的第一个字符在s2中的位置,若不是子串,则返回0.
例:pos(‘ab’,’12abcd’)=3
7. 字符的大写转换。 Upcase(ch) 求字符ch的大写体。
例:upcase(‘a’)=’A’
8. 数值转换为数串 过程 Str(x,s) 把数值x化为数串s.
例:str(12345,s); 结果s=’12345’
9. 数串转换为数值 过程val(s,x,I) 把数串s转化为数值x,如果成功则I=0,不成功则I为无效字符的序数,第三个参数也可不传
例:val(‘1234’,x,I);结果 x:=1234
主要算法
字符串查找算法
正则表达式算法
模式匹配
字符串的模式匹配算法(KMP)
AC自动机
后缀数组/树/自动机
(这是一些字符串处理算法,在字符串上进行不同的处理)
KMP(字符串的模式匹配算法)
KMP算法的名字是由这个算法的三个创始人Knuth、Morris、Pratt名字的首字母缩写而得名的
下面是KMP算法的C语言实现
#include <stdio.h> #include <string.h> #include <stdlib.h> typedef int Position; #define NotFound -1 void BuildMatch( char *pattern, int *match ) { Position i, j; int m = strlen(pattern); match[0] = -1; for ( j=1; j<m; j++ ) { i = match[j-1]; while ( (i>=0) && (pattern[i+1]!=pattern[j]) ) i = match[i]; if ( pattern[i+1]==pattern[j] ) match[j] = i+1; //i回退的总次数不会超过i增加的总次数 else match[j] = -1; } } Position KMP( char *string, char *pattern ) { int n = strlen(string); //O(n) int m = strlen(pattern); //O(m) Position s, p, *match; if ( n < m ) return NotFound; match = (Position *)malloc(sizeof(Position) * m); BuildMatch(pattern, match); //Tm=O(m) s = p = 0; while ( s<n && p<m ) { //O(n) if ( string[s]==pattern[p] ) { s++; p++; } else if (p>0) p = match[p-1]+1; else s++; } return ( p==m )? (s-m) : NotFound; } int main() { char string[] = "This is a simple example."; char pattern[] = "simple"; Position p = KMP(string, pattern); if (p==NotFound) printf("Not Found.\n"); else printf("%s\n", string+p); return 0; }
KMP这个算法的关键在于下面这个BuildMatch函数的实现
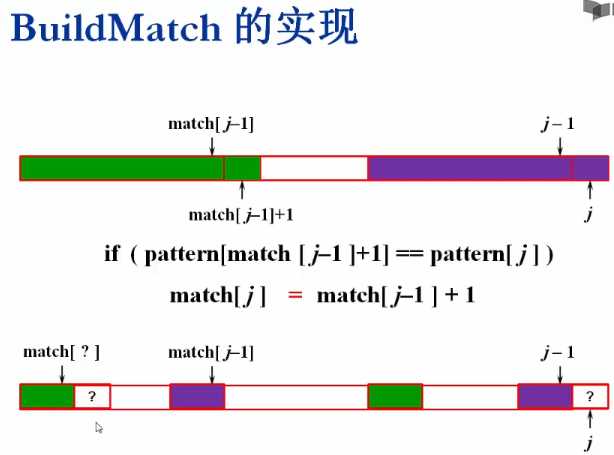
这里有个值得注意的地方
PS:当pattern[match[j-1]+1]!=pattern[j]时,
下一个待与pattern[j]比较的元素下标为:
match[match[j-1]]+1
过程的变化
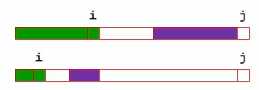


通过对上面的分析我们可以得到KMP算法的时间复杂度为 T=O(n+m)
(这对于形如查找指定文本中的关键字之类的问题而言效率已经很高了哦)
2019-12-22 12:54:08
标签:efi 图片 模式匹配 存储方式 build 关于 后缀数组 程序 lambda
原文地址:https://www.cnblogs.com/StrongAI/p/12079579.html