标签:含义 如何 连续 标准 工作 png == 保存 order
红黑树的起源,自然是二叉查找树了,这种树结构从根节点开始,左子节点小于它,右子节点大于它。每个节点都符合这个特性,所以易于查找,是一种很好的数据结构。但是它有一个问题,就是容易偏向某一侧,这样就像一个链表结构了,失去了树结构的优点,查找时间会变坏。
所以我们都希望树结构都是矮矮胖胖的,像这样:
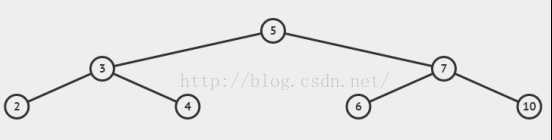
而不是像这样:
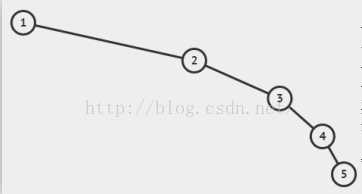
在这种需求下,平衡树(AVL)的概念就应运而生了。
红黑树就是一种平衡树,它可以保证二叉树基本符合矮矮胖胖的结构,但是理解红黑树之前,必须先了解另一种树,叫2-3树,红黑树背后的逻辑就是它。
好吧来看2-3树吧。
2-3树是二叉查找树的变种,树中的2和3代表两种节点,以下表示为2-节点和3-节点。
2-节点即普通节点:包含一个元素,两条子链接。
3-节点则是扩充版,包含2个元素和三条链接:两个元素A、B,左边的链接指向小于A的节点,中间的链接指向介于A、B值之间的节点,右边的链接指向大于B的节点
2-节点:
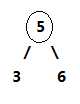
3-节点:
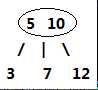
在这两种节点的配合下,2-3树可以保证在插入值过程中,任意叶子节点到根节点的距离都是相同的。完全实现了矮胖矮胖的目标。怎么配合的呢,下面来看2-3树的构造过程。
所谓构造,就是从零开始一个节点一个节点的插入。
在二叉查找树中,插入过程从根节点开始比较,小于节点值往右继续与左子节点比,大于则继续与右子节点比,直到某节点左或右子节点为空,把值插入进去。这样无法避免偏向问题。在2-3树中,插入的过程是这样的。
如果将值插入一个2-节点,则将2-节点扩充为一个3-节点。
如果将值插入一个3-节点,分为以下几种情况。
(1).3-节点没有父节点,即整棵树就只有它一个三节点。此时,将3-节点扩充为一个4-节点,即包含三个元素的节点,然后将其分解,变成一棵二叉树。

此时二叉树依然保持平衡。
(2).3-节点有一个2-节点的父节点,此时的操作是,3-节点扩充为4-节点,然后分解4-节点,然后将分解后的新树的父节点融入到2-节点的父节点中去。

(3).3-节点有一个3-节点的父节点,此时操作是:3-节点扩充为4-节点,然后分解4-节点,新树父节点向上融合,上面的3-节点继续扩充,融合,分解,新树继续向上融合,直到父节点为2-节点为止,如果向上到根节点都是3-节点,将根节点扩充为4-节点,然后分解为新树,至此,整个树增加一层,仍然保持平衡。
第三种情况稍微复杂点,为了便于直观理解,现在我们从零开始构建2-3树,囊括上面所有的情况,看完所以步骤后,你也可以自己画一画。
我们将{7,8,9,10,11,12}中的数值依次插入2-3树,画出它的过程:
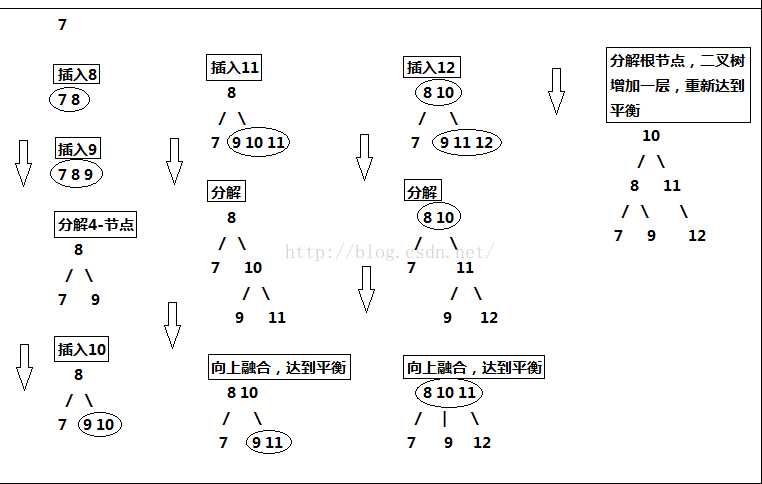
所以,2-3树的设计完全可以保证二叉树保持矮矮胖胖的状态,保持其性能良好。但是,将这种直白的表述写成代码实现起来并不方便,因为要处理的情况太多。这样需要维护两种不同类型的节点,将链接和其他信息从一个节点复制到另一个节点,将节点从一种类型转换为另一种类型等等。
因此,红黑树出现了,红黑树的背后逻辑就是2-3树的逻辑,但是由于用红黑作为标记这个小技巧,最后实现的代码量并不大。(但是,要直接理解这些代码是如何工作的以及背后的道理,就比较困难了。所以你一定要理解它的演化过程,才能真正的理解红黑树)
我们来看看红黑树和2-3树的关联,首先,最台面上的问题,红和黑的含义。红黑树中,所有的节点都是标准的2-节点,为了体现出3-节点,这里将3-节点的两个元素用左斜红色的链接连接起来,即连接了两个2-节点来表示一个3-节点。这里红色节点标记就代表指向其的链接是红链接,黑色标记的节点就是普通的节点。
所以才会有那样一条定义,叫“从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点”,因为红色节点是可以与其父节点合并为一个3-节点的,红黑树实现的其实是一个完美的黑色平衡,如果你将红黑树中所有的红色链接放平,那么它所有的叶子节点到根节点的距离都是相同的。所以它并不是一个严格的平衡二叉树,但是它的综合性能已经很优秀了。
借一张别人的图来看:
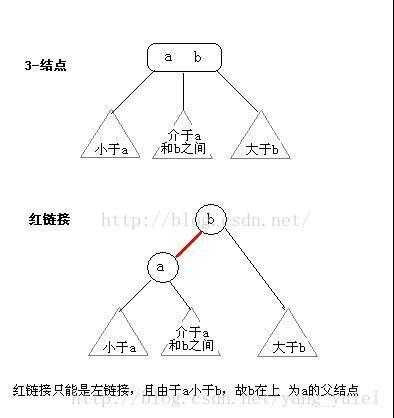
红链接放平:
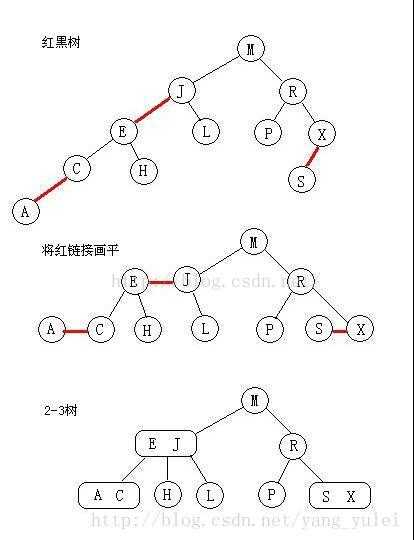
所以,红黑树的另一种定义是满足下列条件的二叉查找树:
⑴红链接均为左链接。
⑵没有任何一个结点同时和两条红链接相连。(这样会出现4-节点)
⑶该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
红黑树是一种特殊的二叉树,且必须要满足以下几个特性:
1. 每个节点或是黑色或是红色
2. 根节点是黑色
3. 每个叶节点是黑色(叶节点为空节点)
4. 如果一个节点是红色,则它的两个子节点必须是黑色
5. 从任意的一个节点到该节点的所有叶节点的路径包含相同数目的黑色节点
6.红黑树是一种平衡二叉树,当不是完全的平衡二叉树,红黑树只要求最多三次旋转来尽可能达到平衡
【也就是说没有规定左子树与右子树的高度差必须<=1!!!!!!】
定理:红黑树的时间复杂度为0(log2n)。
定义:
1.h(v)为以节点v为根节点的子树的高度。
2.bh(v)为从节点v到其子树叶节点路径中黑色节点的数量。
根据特性5可知,bh(v)是唯一值。
又根据特性4可知,从一个节点到其叶节点路径上的黑色节点数目≥路径上的红色节点数目。也就是说h(x)≤2bh(x)
引理:以v为根节点的红黑树,至少有2bh(v)-1 个内部节点。
使用数学归纳法证明引理:
(1)当树的高度h=0时,内部节点个数为0,bh(v)=0,则2bh(v)-1=0,显然满足内部节点个数≥2bh(v)-1.
(2)当h>0,且当h-1时,包含的内部节点数至少为2bh(v)-1-1,
那么对于根节点x,其左子树的内部节点个数至少为2bh(v)-1-1,其右子节点的内部节点个数至少为2bh(v)-1-1,则高度为h,内部节点个数至少为(2bh(v)-1-1)+(2hb(v)-1-1)+1=2bh(v)-1。引理得证。
根据引理可以得出,一个节点数为n的红黑树,bh(v)≤log2(n+1)。又因为h(x)≤2bh(x),可得,h≤2log2(n+1)。
(结论1)红黑树是一种特殊的二又树,对于有n个节点的二又树而言,当其为满二又树时,树的高度最小。
满二又树的节点数量与高度的关系为n=2h-1。
那么可以得出,h≥log2(n+1)。
(结论2)由结论1和结论2可知,log2(n+1)≤h≤2log2(n+1)。
所以,红黑树的时间复杂度为:0(log2n)
红黑树的节点结构与一般的二叉树类似,但是多了一个标记颜色的变量。
1 enum RBTColor{RED, BLACK}; 2 3 template <class T> 4 5 class RBTNode{ 6 7 public: 8 9 RBTColor color; // 颜色 10 11 T key; // 关键字(键值) 12 13 RBTNode *left; // 左孩子 14 15 RBTNode *right; // 右孩子 16 17 RBTNode *parent; // 父结点 18 19 RBTNode(T value, RBTColor c, RBTNode *p, RBTNode *l, RBTNode *r): 20 21 key(value),color(c),parent(),left(l),right(r) {} 22 23 };
红黑树的旋转操作目的是在插入或删除节点后,尽可能的保持红黑树的特性。旋转操作分为左旋和右旋。
左旋操作效果如图所示。左旋操作会使当前节点与其右子节点位置互换。
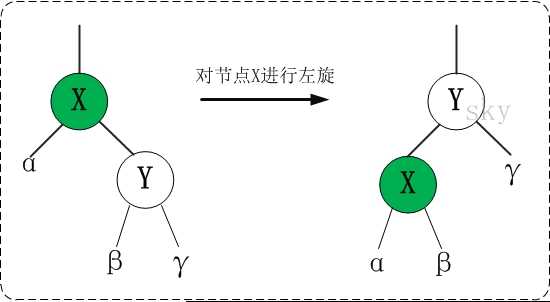
1 template <class T> 2 3 void RBTree<T>::leftRotate(RBTNode<T>* &root, RBTNode<T>* x) 4 5 { 6 7 // 设置x的右孩子为y 8 9 RBTNode<T> *y = x->right; 10 11 // 将 “y的左孩子” 设为 “x的右孩子”; 12 13 // 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲” 14 15 x->right = y->left; 16 17 if (y->left != NULL) 18 19 y->left->parent = x; 20 21 // 将 “x的父亲” 设为 “y的父亲” 22 23 y->parent = x->parent; 24 25 if (x->parent == NULL) 26 27 { 28 29 root = y; // 如果 “x的父亲” 是空节点,则将y设为根节点 30 31 } 32 33 else 34 35 { 36 37 if (x->parent->left == x) 38 39 x->parent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 40 41 else 42 43 x->parent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 44 45 } 46 47 48 49 // 将 “x” 设为 “y的左孩子” 50 51 y->left = x; 52 53 // 将 “x的父节点” 设为 “y” 54 55 x->parent = y; 56 57 }
右旋操作效果如图所示。右旋操作会使当前节点与其左子节点位置互换。
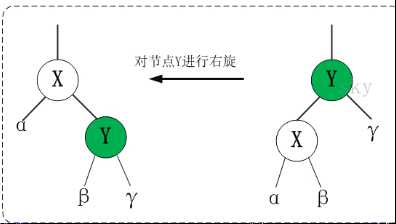
1 template <class T> 2 3 void RBTree<T>::rightRotate(RBTNode<T>* &root, RBTNode<T>* y) 4 5 { 6 7 // 设置x是当前节点的左孩子。 8 9 RBTNode<T> *x = y->left; 10 11 // 将 “x的右孩子” 设为 “y的左孩子”; 12 13 // 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲” 14 15 y->left = x->right; 16 17 if (x->right != NULL) 18 19 x->right->parent = y; 20 21 // 将 “y的父亲” 设为 “x的父亲” 22 23 x->parent = y->parent; 24 25 if (y->parent == NULL) 26 27 { 28 29 root = x; // 如果 “y的父亲” 是空节点,则将x设为根节点 30 31 } 32 33 else 34 35 { 36 37 if (y == y->parent->right) 38 39 y->parent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子” 40 41 else 42 43 y->parent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子” 44 45 } 46 47 // 将 “y” 设为 “x的右孩子” 48 49 x->right = y; 50 51 // 将 “y的父节点” 设为 “x” 52 53 y->parent = x; 54 55 }
本篇文章主要介绍了红黑树的基本概念,包括红黑树的定义、时间复杂度及其证明、节点定义和旋转操作。
红黑树的查找方式很简单,是一个递归过程。如果查找的元素小于当前节点,那么查找其左子树;如果查找的元素大于当前元素,则查找其右子树。查找的时间复杂度为O(log2n)。
(图例:C表示当前节点,P表示父节点,U表示叔节点,G表示祖父节点)
插入操作首先需要通过查找操作找到合适的插入点,然后插入新节点。如果在插入节点后,发生了违背红黑树特性的情况时,需要对红黑树进行旋转染色等操作,使其重新满足特性。
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
红黑树本身就是一颗二叉查找树,将节点插入后,该树仍然是一颗二叉查找树。也就意味着,树的键值仍然是有序的。此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。这也就意味着,任何的旋转和重新着色操作,都不会改变它仍然是一颗二叉查找树的事实。
第二步:将插入的节点着色为"红色"。
为什么着色成红色,而不是黑色呢?为什么呢?我们需要重新温习一下红黑树的特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
将插入的节点着色为红色,不会违背"特性(5)"!少违背一条特性,就意味着我们需要处理的情况越少。接下来,就要努力的让这棵树满足其它性质即可;满足了的话,它就又是一颗红黑树了。
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
第二步中,将插入节点着色为"红色"之后,不会违背"特性(5)"。那它到底会违背哪些特性呢?
对于"特性(1)",显然不会违背了。因为我们已经将它涂成红色了。
对于"特性(2)",显然也不会违背。在第一步中,我们是将红黑树当作二叉查找树,然后执行的插入操作。而根据二叉查找数的特点,插入操作不会改变根节点。所以,根节点仍然是黑色。
对于"特性(3)",显然不会违背了。这里的叶子节点是指的空叶子节点,插入非空节点并不会对它们造成影响。
对于"特性(4)",是有可能违背的!
那接下来,想办法使之"满足特性(4)",就可以将树重新构造成红黑树了。
1 /* 2 3 * 将结点插入到红黑树中 4 5 * 6 7 * 参数说明: 8 9 * root 红黑树的根结点 10 11 * node 插入的结点 12 13 */ 14 15 template <class T> 16 17 void RBTree<T>::insert(RBTNode<T>* &root, RBTNode<T>* node) 18 19 { 20 21 RBTNode<T> *y = NULL; 22 23 RBTNode<T> *x = root; 24 25 // 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。 26 27 while (x != NULL) 28 29 { 30 31 y = x; 32 33 if (node->key < x->key) 34 35 x = x->left; 36 37 else 38 39 x = x->right; 40 41 } 42 43 node->parent = y; 44 45 if (y!=NULL) 46 47 { 48 49 if (node->key < y->key) 50 51 y->left = node; 52 53 else 54 55 y->right = node; 56 57 } 58 59 else 60 61 root = node; 62 63 // 2. 设置节点的颜色为红色 64 65 node->color = RED; 66 67 // 3. 将它重新修正为一颗二叉查找树 68 69 insertFixUp(root, node); 70 71 }
那么,在违反了特性4的时候,新节点的父节点为红色节点。根据特性2可知,父节点不是根节点,则新节点必有祖父节点。
又根据特性3可推论出红色节点必有两个黑色子节点(空节点为黑色)。
此时会出现两种情况:叔节点为红色、叔节点为黑色。
(1)父节点与叔节点都为红色的情况
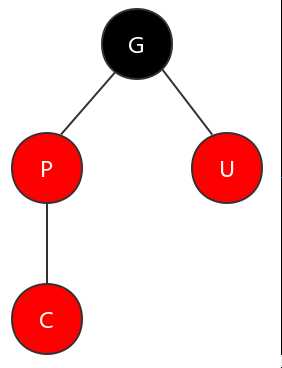
在这种情况下,需要将父节点和叔节点变为黑色,再将祖父节点变为红色。这样,图上所展示的子树就满足了红黑树的特性。如下图所示。
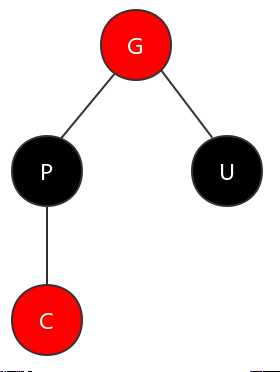
但是这里又可能会产生新的违法特性情况,因为祖父节点变成了红色,那么它可能会造成违反特性4的情况。所以,这里就将祖父节点作为当前节点,进行新一轮的调整操作。
(2)父节点为红色, 叔节点为黑色的情况
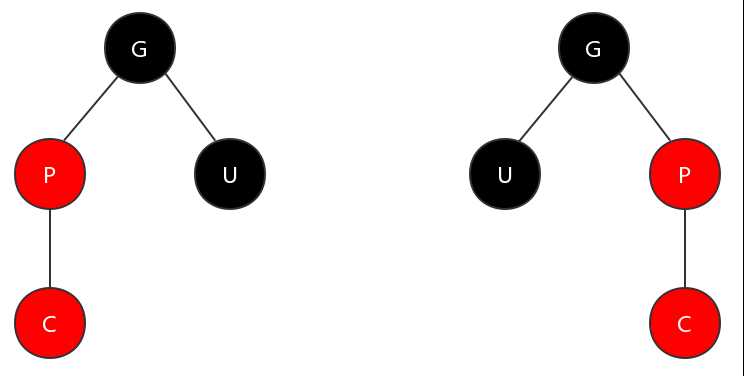
在这种情况下,对其调整的核心就是保持父节点分支符合特性4,而叔节点分支保持符合特性5。
第一步,旋转。对祖父节点进行左旋或者右旋。如果父节点是祖父节点的右子节点,那么对祖父节点进行左旋;否则,对祖父节点进行右旋。
第二步,染色。将祖父节点染为红色,而父节点染为黑色。
进过这两步,上图的情况会转换为下图所示。
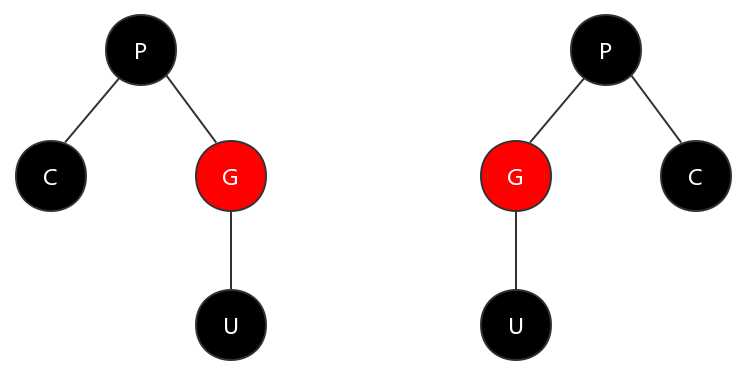
可以看出,父节点这一分支进过调整后,当前节点与父节点的颜色不再是连续红色,满足特性4。而叔节点这一分支的黑色节点数目没有发生变化,满足特性5。
对原祖父节点的父节点来说,该子树没有发生违反特性的变化。该子树调整完成。
当上述调整执行完后,还有最后一步,就是检查是否满足特性2。这一步只需要将根节点染成黑色就可以,无需再多加判断。
1 /* 2 3 * 红黑树插入修正函数 4 5 * 6 7 * 在向红黑树中插入节点之后(失去平衡),再调用该函数; 8 9 * 目的是将它重新塑造成一颗红黑树。 10 11 * 12 13 * 参数说明: 14 15 * root 红黑树的根 16 17 * node 插入的结点 // 对应《算法导论》中的z 18 19 */ 20 21 template <class T> 22 23 void RBTree<T>::insertFixUp(RBTNode<T>* &root, RBTNode<T>* node) 24 25 { 26 27 RBTNode<T> *parent, *gparent; 28 29 // 若“父节点存在,并且父节点的颜色是红色” 30 31 while ((parent = rb_parent(node)) && rb_is_red(parent)) 32 33 { 34 35 gparent = rb_parent(parent); 36 37 //若“父节点”是“祖父节点的左孩子” 38 39 if (parent == gparent->left) 40 41 { 42 43 // Case 1条件:叔叔节点是红色 44 45 { 46 47 RBTNode<T> *uncle = gparent->right; 48 49 if (uncle && rb_is_red(uncle)) 50 51 { 52 53 rb_set_black(uncle); 54 55 rb_set_black(parent); 56 57 rb_set_red(gparent); 58 59 node = gparent; 60 61 continue; 62 63 } 64 65 } 66 67 // Case 2条件:叔叔是黑色,且当前节点是右孩子 68 69 if (parent->right == node) 70 71 { 72 73 RBTNode<T> *tmp; 74 75 leftRotate(root, parent); 76 77 tmp = parent; 78 79 parent = node; 80 81 node = tmp; 82 83 } 84 85 // Case 3条件:叔叔是黑色,且当前节点是左孩子。 86 87 rb_set_black(parent); 88 89 rb_set_red(gparent); 90 91 rightRotate(root, gparent); 92 93 } 94 95 else//若“z的父节点”是“z的祖父节点的右孩子” 96 97 { 98 99 // Case 1条件:叔叔节点是红色 100 101 { 102 103 RBTNode<T> *uncle = gparent->left; 104 105 if (uncle && rb_is_red(uncle)) 106 107 { 108 109 rb_set_black(uncle); 110 111 rb_set_black(parent); 112 113 rb_set_red(gparent); 114 115 node = gparent; 116 117 continue; 118 119 } 120 121 } 122 123 // Case 2条件:叔叔是黑色,且当前节点是左孩子 124 125 if (parent->left == node) 126 127 { 128 129 RBTNode<T> *tmp; 130 131 rightRotate(root, parent); 132 133 tmp = parent; 134 135 parent = node; 136 137 node = tmp; 138 139 } 140 141 // Case 3条件:叔叔是黑色,且当前节点是右孩子。 142 143 rb_set_black(parent); 144 145 rb_set_red(gparent); 146 147 leftRotate(root, gparent); 148 149 } 150 151 } 152 153 // 将根节点设为黑色 154 155 rb_set_black(root); 156 157 }
(图例:D表示当前节点,P表示父节点,B表示兄弟节点,BR表示兄弟节点的右子节点,BL表示兄弟节点的左子节点)
删除操作要比插入操作略微复杂一些。因为删除的节点可能是出现在树的中间层的节点,此时删除该节点会遇到很复杂的情况。所以,在删除节点的时候,需要先对红黑树进行一些调整,使得删除节点对整个树的影响降到最低。
第一步:将红黑树当作一颗二叉查找树,将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况:
① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空,就意味着"该节点的后继节点"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
首先根据BST删除节点的规则,使用当前节点左子树的最大值节点【最右】或者右子树的最小值节点【最左】代替其删除(这两个节点是其子树中数值上最贴近当前节点数值的节点)。
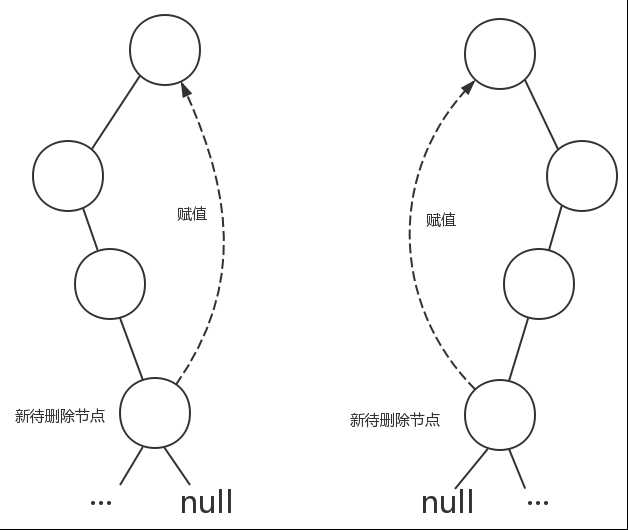
为了方便讲解,我们默认采用的是右子树的最小值节点代替。
那么现在需要考虑的情况就减少了,只可能会出现以下几种情况(因为需要满足红黑树特性):
1. 无子节点,节点为红色
2. 无子节点,节点为黑色
3. 只有右子节点,右子节点为红色,节点本身为黑色
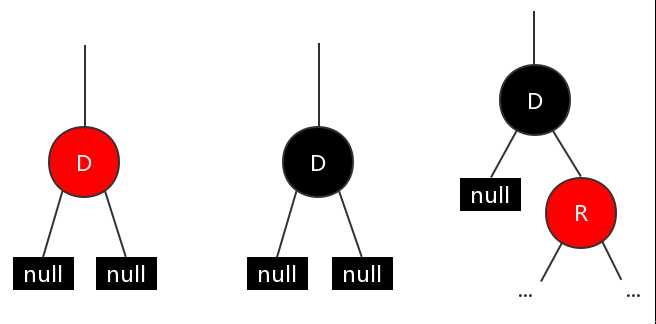
情况1,只需要直接删除节点就可以。
情况2,删除节点后,违反了红黑树特性5,需要调整(不考虑待删除节点为根节点的情况)
情况3,用右子节点占据待删除节点,再将其染成黑色即可,不违反红黑树特性。
在这三种情况中,情况1和情况3比较简单,不需要多余的调整。情况2则需要后续的调整步骤使其满足红黑树特性。
1 /* 2 3 * 删除结点(node),并返回被删除的结点 4 5 * 6 7 * 参数说明: 8 9 * root 红黑树的根结点 10 11 * node 删除的结点 12 13 */ 14 15 template <class T> 16 17 void RBTree<T>::remove(RBTNode<T>* &root, RBTNode<T> *node) 18 19 { 20 21 RBTNode<T> *child, *parent; 22 23 RBTColor color; 24 25 // 被删除节点的"左右孩子都不为空"的情况。 26 27 if ( (node->left!=NULL) && (node->right!=NULL) ) 28 29 { 30 31 // 被删节点的后继节点。(称为"取代节点") 32 33 // 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。 34 35 RBTNode<T> *replace = node; 36 37 // 获取后继节点 38 39 replace = replace->right; 40 41 while (replace->left != NULL) 42 43 replace = replace->left; 44 45 // "node节点"不是根节点(只有根节点不存在父节点) 46 47 if (rb_parent(node)) 48 49 { 50 51 if (rb_parent(node)->left == node) 52 53 rb_parent(node)->left = replace; 54 55 else 56 57 rb_parent(node)->right = replace; 58 59 } 60 61 else 62 63 // "node节点"是根节点,更新根节点。 64 65 root = replace; 66 67 // child是"取代节点"的右孩子,也是需要"调整的节点"。 68 69 // "取代节点"肯定不存在左孩子!因为它是一个后继节点。 70 71 child = replace->right; 72 73 parent = rb_parent(replace); 74 75 // 保存"取代节点"的颜色 76 77 color = rb_color(replace); 78 79 // "被删除节点"是"它的后继节点的父节点" 80 81 if (parent == node) 82 83 { 84 85 parent = replace; 86 87 } 88 89 else 90 91 { 92 93 // child不为空 94 95 if (child) 96 97 rb_set_parent(child, parent); 98 99 parent->left = child; 100 101 replace->right = node->right; 102 103 rb_set_parent(node->right, replace); 104 105 } 106 107 replace->parent = node->parent; 108 109 replace->color = node->color; 110 111 replace->left = node->left; 112 113 node->left->parent = replace; 114 115 if (color == BLACK) 116 117 removeFixUp(root, child, parent); 118 119 delete node; 120 121 return ; 122 123 } 124 125 if (node->left !=NULL) 126 127 child = node->left; 128 129 else 130 131 child = node->right; 132 133 parent = node->parent; 134 135 // 保存"取代节点"的颜色 136 137 color = node->color; 138 139 if (child) 140 141 child->parent = parent; 142 143 // "node节点"不是根节点 144 145 if (parent) 146 147 { 148 149 if (parent->left == node) 150 151 parent->left = child; 152 153 else 154 155 parent->right = child; 156 157 } 158 159 else 160 161 root = child; 162 163 if (color == BLACK) 164 165 removeFixUp(root, child, parent); 166 167 delete node; 168 169 }
上述情况2的调整比较复杂。下面对各种情况进行讲解。
根据红黑树的特性5,待删除节点必然有兄弟节点。下面根据其兄弟节点所在分支的不同,来分情况讨论。
(以下是以关注节点为父节点的左子节点进行描述,如果遇到关注节点为父节点的右子节点的情况,则镜像处理)
(1)兄弟节点为红色
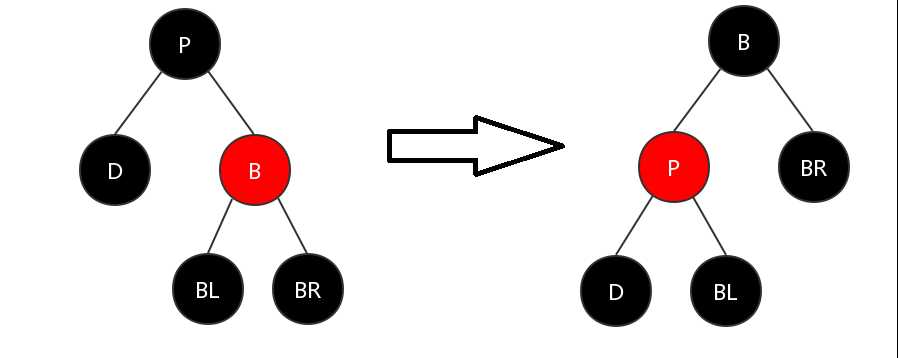
先对父节点进行左旋操作,然后将父节点染成红色,兄弟节点染成黑色。此时就转换为了(4),之后按照(4)继续进行调整。
(2)兄弟节点为黑色,远侄节点为红色
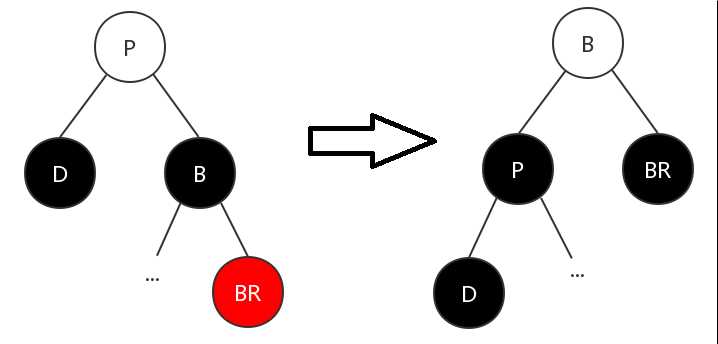
这种情况下,不需要考虑父节点的颜色。
第一步:对父节点P进行左旋操作
第二步:将父节点P与兄弟节点B的颜色互换
第三步:将兄弟节点的右子节点BR染成黑色
可以看到,经过这三步的调整后,直接删除节点D后满足红黑树的特性,调整完成。
(3)兄弟节点为黑色,远侄节点为黑色,近侄节点为红色
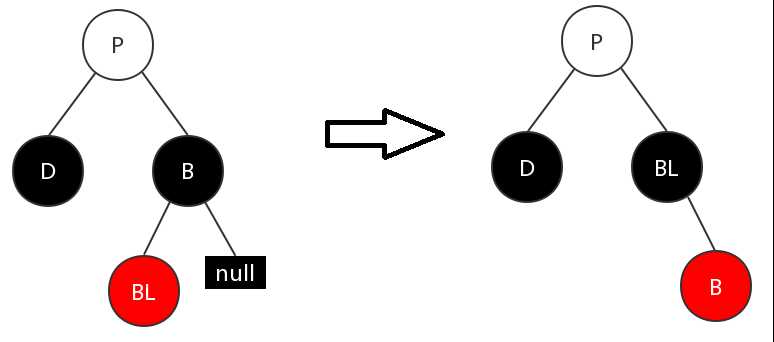
这种情况下,先对兄弟节点B进行右旋操作,然后BL节点染成黑色,B节点染成红色。此时的状况就和(2)一样了。之后就通过(2)的调整方式进行调整。
(4)父节点为红色,兄弟节点为黑色,兄弟节点无子节点
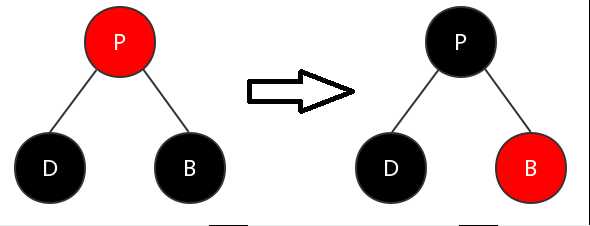
这种情况下,将父节点P染成黑色,再将兄弟节点染成红色。
经过这样的操作后,除去节点D后,以P为根节点的子树的黑节点深度没有发生。调整完成。
(5)父节点为黑色,兄弟节点为黑色,兄弟节点无子节点
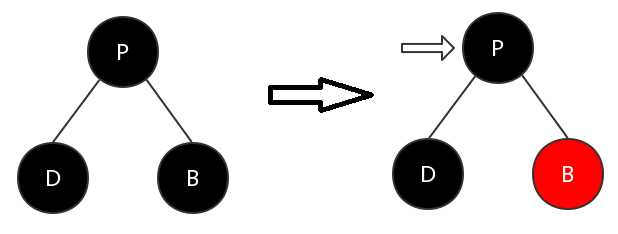
这种情况下,为了在删除节点D后使以P为根节点的子树能满足红黑树特性5,将兄弟节点B染成红色。但是这样操作后,以P为根节点的子树的黑色节点深度变小了。所以需要继续调整。
因为P节点子树的黑色深度发生了减少,可以把其当作待删除节点,那么此时就以P节点为关注节点进行进一步调整。
1 /* 2 3 * 红黑树删除修正函数 4 5 * 6 7 * 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数; 8 9 * 目的是将它重新塑造成一颗红黑树。 10 11 * 12 13 * 参数说明: 14 15 * root 红黑树的根 16 17 * node 待修正的节点 18 19 */ 20 21 template <class T> 22 23 void RBTree<T>::removeFixUp(RBTNode<T>* &root, RBTNode<T> *node, RBTNode<T> *parent) 24 25 { 26 27 RBTNode<T> *other; 28 29 while ((!node || rb_is_black(node)) && node != root) 30 31 { 32 33 if (parent->left == node) 34 35 { 36 37 other = parent->right; 38 39 if (rb_is_red(other)) 40 41 { 42 43 // Case 1: x的兄弟w是红色的 44 45 rb_set_black(other); 46 47 rb_set_red(parent); 48 49 leftRotate(root, parent); 50 51 other = parent->right; 52 53 } 54 55 if ((!other->left || rb_is_black(other->left)) && 56 57 (!other->right || rb_is_black(other->right))) 58 59 { 60 61 // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的 62 63 rb_set_red(other); 64 65 node = parent; 66 67 parent = rb_parent(node); 68 69 } 70 71 else 72 73 { 74 75 if (!other->right || rb_is_black(other->right)) 76 77 { 78 79 // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。 80 81 rb_set_black(other->left); 82 83 rb_set_red(other); 84 85 rightRotate(root, other); 86 87 other = parent->right; 88 89 } 90 91 // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。 92 93 rb_set_color(other, rb_color(parent)); 94 95 rb_set_black(parent); 96 97 rb_set_black(other->right); 98 99 leftRotate(root, parent); 100 101 node = root; 102 103 break; 104 105 } 106 107 } 108 109 else 110 111 { 112 113 other = parent->left; 114 115 if (rb_is_red(other)) 116 117 { 118 119 // Case 1: x的兄弟w是红色的 120 121 rb_set_black(other); 122 123 rb_set_red(parent); 124 125 rightRotate(root, parent); 126 127 other = parent->left; 128 129 } 130 131 if ((!other->left || rb_is_black(other->left)) && 132 133 (!other->right || rb_is_black(other->right))) 134 135 { 136 137 // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的 138 139 rb_set_red(other); 140 141 node = parent; 142 143 parent = rb_parent(node); 144 145 } 146 147 else 148 149 { 150 151 if (!other->left || rb_is_black(other->left)) 152 153 { 154 155 // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。 156 157 rb_set_black(other->right); 158 159 rb_set_red(other); 160 161 leftRotate(root, other); 162 163 other = parent->left; 164 165 } 166 167 // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。 168 169 170 171 rb_set_color(other, rb_color(parent)); 172 173 rb_set_black(parent); 174 175 rb_set_black(other->left); 176 177 rightRotate(root, parent); 178 179 node = root; 180 181 break; 182 183 } 184 185 } 186 187 } 188 189 if (node) 190 191 rb_set_black(node); 192 193 }
经过上述的调整后,此时基本满足了红黑树的特性。但是存在根节点变成红色的情况。所以需要将根节点染成黑色的操作。
最后,执行删除操作,将待删除节点删掉。
本篇文章讲解了红黑树的数据操作,包括除了左旋"、"右旋"、"添加"、"删除"、"遍历"、"查找"、"打印"、"最小值"、"最大值"、"创建"、"销毁"等接口。
注意:
红黑树中的private中的函数都是public中函数的内部实现函数,也就是说,为了确保红黑树的封装,几乎所有的操作都是在内部的私有属性函数中完成的,而public中的函数仅仅只是一个接口而已
1 /** 2 * C++ 语言: 红黑树 3 * 4 * @author skywang 5 * @date 2013/11/07 6 */ 7 #ifndef _RED_BLACK_TREE_HPP_ 8 #define _RED_BLACK_TREE_HPP_ 9 #include <iomanip> 10 #include <iostream> 11 using namespace std; 12 enum RBTColor{RED, BLACK}; 13 template <class T> 14 class RBTNode{ 15 public: 16 RBTColor color; // 颜色 17 T key; // 关键字(键值) 18 RBTNode *left; // 左孩子 19 RBTNode *right; // 右孩子 20 RBTNode *parent; // 父结点 21 RBTNode(T value, RBTColor c, RBTNode *p, RBTNode *l, RBTNode *r): 22 key(value),color(c),parent(),left(l),right(r) {} 23 }; 24 template <class T> 25 class RBTree { 26 private: 27 RBTNode<T> *mRoot; // 根结点 28 public: 29 RBTree(); 30 ~RBTree(); 31 // 前序遍历"红黑树" 32 void preOrder(); 33 // 中序遍历"红黑树" 34 void inOrder(); 35 // 后序遍历"红黑树" 36 void postOrder(); 37 // (递归实现)查找"红黑树"中键值为key的节点 38 RBTNode<T>* search(T key); 39 // (非递归实现)查找"红黑树"中键值为key的节点 40 RBTNode<T>* iterativeSearch(T key); 41 // 查找最小结点:返回最小结点的键值。 42 T minimum(); 43 // 查找最大结点:返回最大结点的键值。 44 T maximum(); 45 // 找结点(x)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。 46 RBTNode<T>* successor(RBTNode<T> *x); 47 // 找结点(x)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。 48 RBTNode<T>* predecessor(RBTNode<T> *x); 49 // 将结点(key为节点键值)插入到红黑树中 50 void insert(T key); 51 // 删除结点(key为节点键值) 52 void remove(T key); 53 // 销毁红黑树 54 void destroy(); 55 // 打印红黑树 56 void print(); 57 private: 58 // 前序遍历"红黑树" 59 void preOrder(RBTNode<T>* tree) const; 60 // 中序遍历"红黑树" 61 void inOrder(RBTNode<T>* tree) const; 62 // 后序遍历"红黑树" 63 void postOrder(RBTNode<T>* tree) const; 64 // (递归实现)查找"红黑树x"中键值为key的节点 65 RBTNode<T>* search(RBTNode<T>* x, T key) const; 66 // (非递归实现)查找"红黑树x"中键值为key的节点 67 RBTNode<T>* iterativeSearch(RBTNode<T>* x, T key) const; 68 // 查找最小结点:返回tree为根结点的红黑树的最小结点。 69 RBTNode<T>* minimum(RBTNode<T>* tree); 70 // 查找最大结点:返回tree为根结点的红黑树的最大结点。 71 RBTNode<T>* maximum(RBTNode<T>* tree); 72 // 左旋 73 void leftRotate(RBTNode<T>* &root, RBTNode<T>* x); 74 // 右旋 75 void rightRotate(RBTNode<T>* &root, RBTNode<T>* y); 76 // 插入函数 77 void insert(RBTNode<T>* &root, RBTNode<T>* node); 78 // 插入修正函数 79 void insertFixUp(RBTNode<T>* &root, RBTNode<T>* node); 80 // 删除函数 81 void remove(RBTNode<T>* &root, RBTNode<T> *node); 82 // 删除修正函数 83 void removeFixUp(RBTNode<T>* &root, RBTNode<T> *node, RBTNode<T> *parent); 84 // 销毁红黑树 85 void destroy(RBTNode<T>* &tree); 86 // 打印红黑树 87 void print(RBTNode<T>* tree, T key, int direction); 88 #define rb_parent(r) ((r)->parent) 89 #define rb_color(r) ((r)->color) 90 #define rb_is_red(r) ((r)->color==RED) 91 #define rb_is_black(r) ((r)->color==BLACK) 92 #define rb_set_black(r) do { (r)->color = BLACK; } while (0) 93 #define rb_set_red(r) do { (r)->color = RED; } while (0) 94 #define rb_set_parent(r,p) do { (r)->parent = (p); } while (0) 95 #define rb_set_color(r,c) do { (r)->color = (c); } while (0) 96 }; 97 /* 98 * 构造函数 99 */ 100 template <class T> 101 RBTree<T>::RBTree():mRoot(NULL) 102 { 103 mRoot = NULL; 104 } 105 /* 106 * 析构函数 107 */ 108 template <class T> 109 RBTree<T>::~RBTree() 110 { 111 destroy(); 112 } 113 /* 114 * 前序遍历"红黑树" 115 */ 116 template <class T> 117 void RBTree<T>::preOrder(RBTNode<T>* tree) const 118 { 119 if(tree != NULL) 120 { 121 cout<< tree->key << " " ; 122 preOrder(tree->left); 123 preOrder(tree->right); 124 } 125 } 126 template <class T> 127 void RBTree<T>::preOrder() 128 { 129 preOrder(mRoot); 130 } 131 /* 132 * 中序遍历"红黑树" 133 */ 134 template <class T> 135 void RBTree<T>::inOrder(RBTNode<T>* tree) const 136 { 137 if(tree != NULL) 138 { 139 inOrder(tree->left); 140 cout<< tree->key << " " ; 141 inOrder(tree->right); 142 } 143 } 144 template <class T> 145 void RBTree<T>::inOrder() 146 { 147 inOrder(mRoot); 148 } 149 /* 150 * 后序遍历"红黑树" 151 */ 152 template <class T> 153 void RBTree<T>::postOrder(RBTNode<T>* tree) const 154 { 155 if(tree != NULL) 156 { 157 postOrder(tree->left); 158 postOrder(tree->right); 159 cout<< tree->key << " " ; 160 } 161 } 162 template <class T> 163 void RBTree<T>::postOrder() 164 { 165 postOrder(mRoot); 166 } 167 /* 168 * (递归实现)查找"红黑树x"中键值为key的节点 169 */ 170 template <class T> 171 RBTNode<T>* RBTree<T>::search(RBTNode<T>* x, T key) const 172 { 173 if (x==NULL || x->key==key) 174 return x; 175 if (key < x->key) 176 return search(x->left, key); 177 else 178 return search(x->right, key); 179 } 180 template <class T> 181 RBTNode<T>* RBTree<T>::search(T key) 182 { 183 search(mRoot, key); 184 } 185 /* 186 * (非递归实现)查找"红黑树x"中键值为key的节点 187 */ 188 template <class T> 189 RBTNode<T>* RBTree<T>::iterativeSearch(RBTNode<T>* x, T key) const 190 { 191 while ((x!=NULL) && (x->key!=key)) 192 { 193 if (key < x->key) 194 x = x->left; 195 else 196 x = x->right; 197 } 198 return x; 199 } 200 template <class T> 201 RBTNode<T>* RBTree<T>::iterativeSearch(T key) 202 { 203 iterativeSearch(mRoot, key); 204 } 205 /* 206 * 查找最小结点:返回tree为根结点的红黑树的最小结点。 207 */ 208 template <class T> 209 RBTNode<T>* RBTree<T>::minimum(RBTNode<T>* tree) 210 { 211 if (tree == NULL) 212 return NULL; 213 while(tree->left != NULL) 214 tree = tree->left; 215 return tree; 216 } 217 template <class T> 218 T RBTree<T>::minimum() 219 { 220 RBTNode<T> *p = minimum(mRoot); 221 if (p != NULL) 222 return p->key; 223 return (T)NULL; 224 } 225 226 /* 227 * 查找最大结点:返回tree为根结点的红黑树的最大结点。 228 */ 229 template <class T> 230 RBTNode<T>* RBTree<T>::maximum(RBTNode<T>* tree) 231 { 232 if (tree == NULL) 233 return NULL; 234 while(tree->right != NULL) 235 tree = tree->right; 236 return tree; 237 } 238 template <class T> 239 T RBTree<T>::maximum() 240 { 241 RBTNode<T> *p = maximum(mRoot); 242 if (p != NULL) 243 return p->key; 244 return (T)NULL; 245 } 246 /* 247 * 找结点(x)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。 248 */ 249 template <class T> 250 RBTNode<T>* RBTree<T>::successor(RBTNode<T> *x) 251 { 252 // 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。 253 if (x->right != NULL) 254 return minimum(x->right); 255 // 如果x没有右孩子。则x有以下两种可能: 256 // (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。 257 // (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。 258 RBTNode<T>* y = x->parent; 259 while ((y!=NULL) && (x==y->right)) 260 { 261 x = y; 262 y = y->parent; 263 } 264 return y; 265 } 266 267 /* 268 * 找结点(x)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。 269 */ 270 template <class T> 271 RBTNode<T>* RBTree<T>::predecessor(RBTNode<T> *x) 272 { 273 // 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。 274 if (x->left != NULL) 275 return maximum(x->left); 276 // 如果x没有左孩子。则x有以下两种可能: 277 // (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。 278 // (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。 279 RBTNode<T>* y = x->parent; 280 while ((y!=NULL) && (x==y->left)) 281 { 282 x = y; 283 y = y->parent; 284 } 285 return y; 286 } 287 /* 288 * 对红黑树的节点(x)进行左旋转 289 * 290 * 左旋示意图(对节点x进行左旋): 291 * px px 292 * / / 293 * x y 294 * / \ --(左旋)--> / \ # 295 * lx y x ry 296 * / \ / 297 * ly ry lx ly 298 * 299 * 300 */ 301 template <class T> 302 void RBTree<T>::leftRotate(RBTNode<T>* &root, RBTNode<T>* x) 303 { 304 // 设置x的右孩子为y 305 RBTNode<T> *y = x->right; 306 // 将 “y的左孩子” 设为 “x的右孩子”; 307 // 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲” 308 x->right = y->left; 309 if (y->left != NULL) 310 y->left->parent = x; 311 // 将 “x的父亲” 设为 “y的父亲” 312 y->parent = x->parent; 313 if (x->parent == NULL) 314 { 315 root = y; // 如果 “x的父亲” 是空节点,则将y设为根节点 316 } 317 else 318 { 319 if (x->parent->left == x) 320 x->parent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 321 else 322 x->parent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 323 } 324 325 // 将 “x” 设为 “y的左孩子” 326 y->left = x; 327 // 将 “x的父节点” 设为 “y” 328 x->parent = y; 329 } 330 /* 331 * 对红黑树的节点(y)进行右旋转 332 * 333 * 右旋示意图(对节点y进行左旋): 334 * py py 335 * / / 336 * y x 337 * / \ --(右旋)--> / \ # 338 * x ry lx y 339 * / \ / \ # 340 * lx rx rx ry 341 * 342 */ 343 template <class T> 344 void RBTree<T>::rightRotate(RBTNode<T>* &root, RBTNode<T>* y) 345 { 346 // 设置x是当前节点的左孩子。 347 RBTNode<T> *x = y->left; 348 // 将 “x的右孩子” 设为 “y的左孩子”; 349 // 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲” 350 y->left = x->right; 351 if (x->right != NULL) 352 x->right->parent = y; 353 // 将 “y的父亲” 设为 “x的父亲” 354 x->parent = y->parent; 355 if (y->parent == NULL) 356 { 357 root = x; // 如果 “y的父亲” 是空节点,则将x设为根节点 358 } 359 else 360 { 361 if (y == y->parent->right) 362 y->parent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子” 363 else 364 y->parent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子” 365 } 366 // 将 “y” 设为 “x的右孩子” 367 x->right = y; 368 // 将 “y的父节点” 设为 “x” 369 y->parent = x; 370 } 371 /* 372 * 红黑树插入修正函数 373 * 374 * 在向红黑树中插入节点之后(失去平衡),再调用该函数; 375 * 目的是将它重新塑造成一颗红黑树。 376 * 377 * 参数说明: 378 * root 红黑树的根 379 * node 插入的结点 // 对应《算法导论》中的z 380 */ 381 template <class T> 382 void RBTree<T>::insertFixUp(RBTNode<T>* &root, RBTNode<T>* node) 383 { 384 RBTNode<T> *parent, *gparent; 385 // 若“父节点存在,并且父节点的颜色是红色” 386 while ((parent = rb_parent(node)) && rb_is_red(parent)) 387 { 388 gparent = rb_parent(parent); 389 //若“父节点”是“祖父节点的左孩子” 390 if (parent == gparent->left) 391 { 392 // Case 1条件:叔叔节点是红色 393 { 394 RBTNode<T> *uncle = gparent->right; 395 if (uncle && rb_is_red(uncle)) 396 { 397 rb_set_black(uncle); 398 rb_set_black(parent); 399 rb_set_red(gparent); 400 node = gparent; 401 continue; 402 } 403 } 404 // Case 2条件:叔叔是黑色,且当前节点是右孩子 405 if (parent->right == node) 406 { 407 RBTNode<T> *tmp; 408 leftRotate(root, parent); 409 tmp = parent; 410 parent = node; 411 node = tmp; 412 } 413 // Case 3条件:叔叔是黑色,且当前节点是左孩子。 414 rb_set_black(parent); 415 rb_set_red(gparent); 416 rightRotate(root, gparent); 417 } 418 else//若“z的父节点”是“z的祖父节点的右孩子” 419 { 420 // Case 1条件:叔叔节点是红色 421 { 422 RBTNode<T> *uncle = gparent->left; 423 if (uncle && rb_is_red(uncle)) 424 { 425 rb_set_black(uncle); 426 rb_set_black(parent); 427 rb_set_red(gparent); 428 node = gparent; 429 continue; 430 } 431 } 432 // Case 2条件:叔叔是黑色,且当前节点是左孩子 433 if (parent->left == node) 434 { 435 RBTNode<T> *tmp; 436 rightRotate(root, parent); 437 tmp = parent; 438 parent = node; 439 node = tmp; 440 } 441 // Case 3条件:叔叔是黑色,且当前节点是右孩子。 442 rb_set_black(parent); 443 rb_set_red(gparent); 444 leftRotate(root, gparent); 445 } 446 } 447 // 将根节点设为黑色 448 rb_set_black(root); 449 } 450 /* 451 * 将结点插入到红黑树中 452 * 453 * 参数说明: 454 * root 红黑树的根结点 455 * node 插入的结点 // 对应《算法导论》中的node 456 */ 457 template <class T> 458 void RBTree<T>::insert(RBTNode<T>* &root, RBTNode<T>* node) 459 { 460 RBTNode<T> *y = NULL; 461 RBTNode<T> *x = root; 462 // 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。 463 while (x != NULL) 464 { 465 y = x; 466 if (node->key < x->key) 467 x = x->left; 468 else 469 x = x->right; 470 } 471 node->parent = y; 472 if (y!=NULL) 473 { 474 if (node->key < y->key) 475 y->left = node; 476 else 477 y->right = node; 478 } 479 else 480 root = node; 481 // 2. 设置节点的颜色为红色 482 node->color = RED; 483 // 3. 将它重新修正为一颗二叉查找树 484 insertFixUp(root, node); 485 } 486 /* 487 * 将结点(key为节点键值)插入到红黑树中 488 * 489 * 参数说明: 490 * tree 红黑树的根结点 491 * key 插入结点的键值 492 */ 493 template <class T> 494 void RBTree<T>::insert(T key) 495 { 496 RBTNode<T> *z=NULL; 497 // 如果新建结点失败,则返回。 498 if ((z=new RBTNode<T>(key,BLACK,NULL,NULL,NULL)) == NULL) 499 return ; 500 insert(mRoot, z); 501 } 502 /* 503 * 红黑树删除修正函数 504 * 505 * 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数; 506 * 目的是将它重新塑造成一颗红黑树。 507 * 508 * 参数说明: 509 * root 红黑树的根 510 * node 待修正的节点 511 */ 512 template <class T> 513 void RBTree<T>::removeFixUp(RBTNode<T>* &root, RBTNode<T> *node, RBTNode<T> *parent) 514 { 515 RBTNode<T> *other; 516 while ((!node || rb_is_black(node)) && node != root) 517 { 518 if (parent->left == node) 519 { 520 other = parent->right; 521 if (rb_is_red(other)) 522 { 523 // Case 1: x的兄弟w是红色的 524 rb_set_black(other); 525 rb_set_red(parent); 526 leftRotate(root, parent); 527 other = parent->right; 528 } 529 if ((!other->left || rb_is_black(other->left)) && 530 (!other->right || rb_is_black(other->right))) 531 { 532 // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的 533 rb_set_red(other); 534 node = parent; 535 parent = rb_parent(node); 536 } 537 else 538 { 539 if (!other->right || rb_is_black(other->right)) 540 { 541 // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。 542 rb_set_black(other->left); 543 rb_set_red(other); 544 rightRotate(root, other); 545 other = parent->right; 546 } 547 // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。 548 rb_set_color(other, rb_color(parent)); 549 rb_set_black(parent); 550 rb_set_black(other->right); 551 leftRotate(root, parent); 552 node = root; 553 break; 554 } 555 } 556 else 557 { 558 other = parent->left; 559 if (rb_is_red(other)) 560 { 561 // Case 1: x的兄弟w是红色的 562 rb_set_black(other); 563 rb_set_red(parent); 564 rightRotate(root, parent); 565 other = parent->left; 566 } 567 if ((!other->left || rb_is_black(other->left)) && 568 (!other->right || rb_is_black(other->right))) 569 { 570 // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的 571 rb_set_red(other); 572 node = parent; 573 parent = rb_parent(node); 574 } 575 else 576 { 577 if (!other->left || rb_is_black(other->left)) 578 { 579 // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。 580 rb_set_black(other->right); 581 rb_set_red(other); 582 leftRotate(root, other); 583 other = parent->left; 584 } 585 // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。 586 rb_set_color(other, rb_color(parent)); 587 rb_set_black(parent); 588 rb_set_black(other->left); 589 rightRotate(root, parent); 590 node = root; 591 break; 592 } 593 } 594 } 595 if (node) 596 rb_set_black(node); 597 } 598 /* 599 * 删除结点(node),并返回被删除的结点 600 * 601 * 参数说明: 602 * root 红黑树的根结点 603 * node 删除的结点 604 */ 605 template <class T> 606 void RBTree<T>::remove(RBTNode<T>* &root, RBTNode<T> *node) 607 { 608 RBTNode<T> *child, *parent; 609 RBTColor color; 610 // 被删除节点的"左右孩子都不为空"的情况。 611 if ( (node->left!=NULL) && (node->right!=NULL) ) 612 { 613 // 被删节点的后继节点。(称为"取代节点") 614 // 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。 615 RBTNode<T> *replace = node; 616 // 获取后继节点 617 replace = replace->right; 618 while (replace->left != NULL) 619 replace = replace->left; 620 // "node节点"不是根节点(只有根节点不存在父节点) 621 if (rb_parent(node)) 622 { 623 if (rb_parent(node)->left == node) 624 rb_parent(node)->left = replace; 625 else 626 rb_parent(node)->right = replace; 627 } 628 else 629 // "node节点"是根节点,更新根节点。 630 root = replace; 631 // child是"取代节点"的右孩子,也是需要"调整的节点"。 632 // "取代节点"肯定不存在左孩子!因为它是一个后继节点。 633 child = replace->right; 634 parent = rb_parent(replace); 635 // 保存"取代节点"的颜色 636 color = rb_color(replace); 637 // "被删除节点"是"它的后继节点的父节点" 638 if (parent == node) 639 { 640 parent = replace; 641 } 642 else 643 { 644 // child不为空 645 if (child) 646 rb_set_parent(child, parent); 647 parent->left = child; 648 replace->right = node->right; 649 rb_set_parent(node->right, replace); 650 } 651 replace->parent = node->parent; 652 replace->color = node->color; 653 replace->left = node->left; 654 node->left->parent = replace; 655 if (color == BLACK) 656 removeFixUp(root, child, parent); 657 delete node; 658 return ; 659 } 660 if (node->left !=NULL) 661 child = node->left; 662 else 663 child = node->right; 664 parent = node->parent; 665 // 保存"取代节点"的颜色 666 color = node->color; 667 if (child) 668 child->parent = parent; 669 // "node节点"不是根节点 670 if (parent) 671 { 672 if (parent->left == node) 673 parent->left = child; 674 else 675 parent->right = child; 676 } 677 else 678 root = child; 679 if (color == BLACK) 680 removeFixUp(root, child, parent); 681 delete node; 682 } 683 /* 684 * 删除红黑树中键值为key的节点 685 * 686 * 参数说明: 687 * tree 红黑树的根结点 688 */ 689 template <class T> 690 void RBTree<T>::remove(T key) 691 { 692 RBTNode<T> *node; 693 // 查找key对应的节点(node),找到的话就删除该节点 694 if ((node = search(mRoot, key)) != NULL) 695 remove(mRoot, node); 696 } 697 /* 698 * 销毁红黑树 699 */ 700 template <class T> 701 void RBTree<T>::destroy(RBTNode<T>* &tree) 702 { 703 if (tree==NULL) 704 return ; 705 if (tree->left != NULL) 706 return destroy(tree->left); 707 if (tree->right != NULL) 708 return destroy(tree->right); 709 delete tree; 710 tree=NULL; 711 } 712 template <class T> 713 void RBTree<T>::destroy() 714 { 715 destroy(mRoot); 716 } 717 /* 718 * 打印"二叉查找树" 719 * 720 * key -- 节点的键值 721 * direction -- 0,表示该节点是根节点; 722 * -1,表示该节点是它的父结点的左孩子; 723 * 1,表示该节点是它的父结点的右孩子。 724 */ 725 template <class T> 726 void RBTree<T>::print(RBTNode<T>* tree, T key, int direction) 727 { 728 if(tree != NULL) 729 { 730 if(direction==0) // tree是根节点 731 cout << setw(2) << tree->key << "(B) is root" << endl; 732 else // tree是分支节点 733 cout << setw(2) << tree->key << (rb_is_red(tree)?"(R)":"(B)") << " is " << setw(2) << key << "‘s " << setw(12) << (direction==1?"right child" : "left child") << endl; 734 print(tree->left, tree->key, -1); 735 print(tree->right,tree->key, 1); 736 } 737 } 738 739 template <class T> 740 void RBTree<T>::print() 741 { 742 if (mRoot != NULL) 743 print(mRoot, mRoot->key, 0); 744 } 745 #endif
标签:含义 如何 连续 标准 工作 png == 保存 order
原文地址:https://www.cnblogs.com/zzw1024/p/12081711.html