标签:互斥量 基础上 规则 基础 避免死锁 一个 顺序 llb 资源
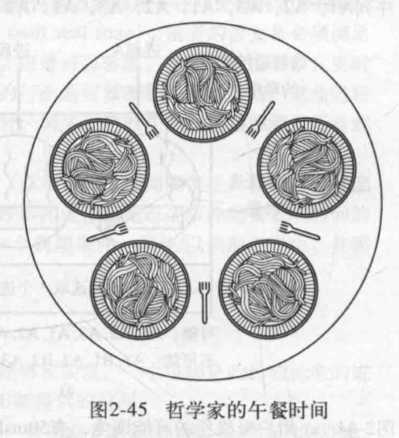
如上图,有五位哲学家,盘中的食物只有左右两个叉子都拿起才能吃。哲学家在桌上只有思考(等待)和吃面(执行)。看起来最多是只有2个人能同时吃。

版本一:这个思路的最糟糕的就是都拿起左边叉子,那样都没法吃了,直接死锁。
版本二:改进版本一,如果拿起左边叉子,先看右边是否能用,不可用的话放下左边叉子等待一段时间再运行。这个思路的问题就是,会产生某个时刻每个人都拿起左叉子,又放下,又拿起,虽然没有死锁,但是没有人在吃面,消耗了性能但是任务没有进展,造成饥饿。
版本三:改进版本二,每次等待右边是否能用的每个哲学家(线程)时间不一样,这个方法看起来ok,但是考虑到极度糟糕情况下,它仍不能稳定,对于极度要求稳定的场合显然也是不合适的。
版本四:我们可以对think后加一个互斥量,就是在拿起左叉子前,就加上一个互斥量,别人就没法拿叉子了,放下互斥量在去掉,但问题是性能差,一次只能有一位人吃面,一开始我们就分析过其实可以两个人同时吃的。

这是新的解法:其实就是在版本四的基础上对每个要拿起叉子的哲学家进行了left 和 right的饥饿状态判断,只有当邻居都不在饮食的基础上才能饮食。这样既不会死锁也不会饥饿,且性能满足了。
下面为Wiki的解释和方法:
一个简单的解法是引入一个餐厅服务生,哲学家必须经过他的允许才能拿起餐叉。因为服务生知道哪只餐叉正在使用,所以他能够作出判断避免死锁。
为了演示这种解法,假设哲学家依次标号为A至E。如果A和C在吃东西,则有四只餐叉在使用中。B坐在A和C之间,所以两只餐叉都无法使用,而D和E之间有一只空余的餐叉。假设这时D想要吃东西。如果他拿起了第五只餐叉,就有可能发生死锁。相反,如果他征求服务生同意,服务生会让他等待。这样,我们就能保证下次当两把餐叉空余出来时,一定有一位哲学家可以成功的得到一对餐叉,从而避免了死锁。
另一个简单的解法是为资源(这里是餐叉)分配一个偏序或者分级的关系,并约定所有资源都按照这种顺序获取,按相反顺序释放,而且保证不会有两个无关资源同时被同一项工作所需要。在哲学家就餐问题中,资源(餐叉)按照某种规则编号为1至5,每一个工作单元(哲学家)总是先拿起左右两边编号较低的餐叉,再拿编号较高的。用完餐叉后,他总是先放下编号较高的餐叉,再放下编号较低的。在这种情况下,当四位哲学家同时拿起他们手边编号较低的餐叉时,只有编号最高的餐叉留在桌上,从而第五位哲学家就不能使用任何一只餐叉了。而且,只有一位哲学家能使用最高编号的餐叉,所以他能使用两只餐叉用餐。当他吃完后,他会先放下编号最高的餐叉,再放下编号较低的餐叉,从而让另一位哲学家拿起后边的这只开始吃东西。
尽管资源分级能避免死锁,但这种策略并不总是实用的,特别是当所需资源的列表并不是事先知道的时候。例如,假设一个工作单元拿着资源3和5,并决定需要资源2,则必须先要释放5,之后释放3,才能得到2,之后必须重新按顺序获取3和5。对需要访问大量数据库记录的计算机程序来说,如果需要先释放高编号的记录才能访问新的记录,那么运行效率就不会高,因此这种方法在这里并不实用。
1984年,K. Mani Chandy和J. Misra提出了哲学家就餐问题的另一个解法,允许任意的用户(编号{\displaystyle P_{1},\cdots ,P_{n}}
这个解法允许很大的并行性,适用于任意大的问题。
标签:互斥量 基础上 规则 基础 避免死锁 一个 顺序 llb 资源
原文地址:https://www.cnblogs.com/CherryTab/p/12088495.html