AVL树

标签：dir   index   The   左右   ade   怎么   and   link   插入   

AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O（log n）。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

AVL数在插入或删除节点之后很可能对不再平衡，这时，需要进行几次所谓的“AVL”旋转。以下图表以四列表示四种情况，每行表示在该种情况下要进行的操作。在左左和右右的情况下，只需要进行一次旋转操作；在左右和右左的情况下，需要进行两次旋转操作。

插入

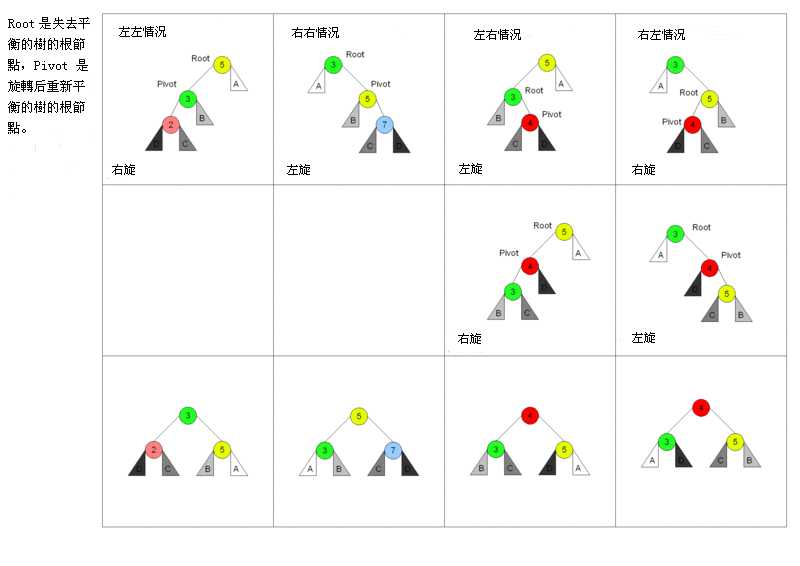
向AVL树插入可以通过如同它是未平衡的二叉查找树一样把给定的值插入树中，接着自底向上向根节点折回，于在插入期间成为不平衡的所有节点上进行旋转来完成。因为折回到根节点的路途上最多有1.44乘log n个节点，而每次AVL旋转都耗费恒定的时间，插入处理在整体上耗费O(log n) 时间。

删除

从AVL树中删除可以通过把要删除的节点向下旋转成一个叶子节点，接着直接剪除这个叶子节点来完成。因为在旋转成叶子节点期间最多有log n个节点被旋转，而每次AVL旋转耗费恒定的时间，删除处理在整体上耗费O(log n) 时间。

以上均引自维基百科：http://zh.wikipedia.org/wiki/AVL%E6%A0%91

插入思路：

       向AVL树插入是个查找寻位的过程，right 或 left，比较容易实现。但插入之后，寻路路过的节点的平衡因子可能会改变，从而导致树不再平衡，这时候就需对不平衡的节点进行旋转。

       问题是怎么确定不平衡的节点，即不平衡的树是的root节点在哪里？

       已知在平衡因子为0的节点的子树任一位置插入一个节点，该节点的平衡因子变换只是在-1，0，1之间，由此可得，不平衡树的root节点平衡因子不为0.从root节点开始，寻位路过的节点的平衡因子均会改变。

       旋转要做的就是把root子树整平衡。此需要知道几个元素：

       1. 指向不平衡树root节点，指向root节点的parent(可由变量 r、p保存，寻位时，出现平衡因子不为0的节点更新）

       2. 插入节点后，从root开始，各节点的平衡因子(可有数组保存每次寻位是left还是right，然后平衡因子相应加减1）

       更新平衡因子之后，判断root的平衡因子，若不为正负2，直接返回，若是，就根据上图四中情况进行旋转。

      注意点：左右、右左情况旋转后平衡因子的更新。

删除思路：

　　从AVL树中删除可以通过把要删除的节点向下旋转成一个叶子节点，接着直接剪除这个叶子节点来完成。然后根据寻路

路径，由下向上进行如下步骤：

     1. 更新平衡因子

     2. 判断，是否影响Parent的平衡因子，未影响则退出。

     3. 旋转，再进行步骤 2，若还有影响，则进行步骤4

     4. 对Parent进行步骤 1（奈何不知道在哪里画流程图^_^）

     另一种表达方式：

           删除的节点向下旋转成一个叶子节点即为一个叶子节点和待删除节点交换位置。

           定义：待删除节点del_node, 待交换的叶子节点swap_node

     可以推测swap_node需为del_node左子树的最大值或右子树的最大值。

AVL树

标签：dir   index   The   左右   ade   怎么   and   link   插入   

原文地址：https://www.cnblogs.com/minikobe/p/12106059.html