标签:不同 向量 使用 name htm org matrix blog 衡量
PCA的流程:
代码参考:https://www.cnblogs.com/clnchanpin/p/7199713.html
协方差矩阵的计算
https://docs.scipy.org/doc/numpy/reference/generated/numpy.cov.html


思想:
https://www.cnblogs.com/clnchanpin/p/7199713.html
求解协方差矩阵的特征值和特征向量
为什么PCA第一步是进行去掉数据中的平均值?
因为每列数据减去该列的平均值后才能进行协方差计算。
按照特征值的大小进行排序,用到了numpy 中argsort函数

https://blog.csdn.net/maoersong/article/details/21875705
这篇对numpy中的matrix 总结的很好
https://www.cnblogs.com/sumuncle/p/5760458.html
(1)方差、协方差、相关系数、协方差矩阵
方差: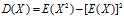
协方差: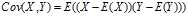 ,
, 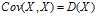 ,
, 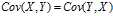
**方差是衡量单变量的离散程度,协方差是衡量两个变量的相关程度(亲疏),协方差越大表明两个变量越相似(亲密),协方差越小表明两个变量之间相互独立的程度越大。
相关系数: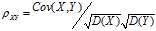 ,
,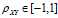
**协方差和相关系数都可以衡量两个表明的相关程度,协方差未消除量纲,不同变量之间的协方差大小不能直接比较,而相关系数消除了量纲,可以比较不同变量之间的相关程度。
摘自——https://blog.csdn.net/weixin_37721518/article/details/79016226
使用python计算协方差的相关系数
https://blog.csdn.net/theonegis/article/details/85059105
标签:不同 向量 使用 name htm org matrix blog 衡量
原文地址:https://www.cnblogs.com/JasonPeng1/p/12110145.html