标签:定义 很多 idt ubi 变化 速度慢 怎么 假设 起点
cubic-bezier
三次贝塞尔曲线函数,是一种动画的速度曲线。根据动画设置的时间,速度相应变化
四个点
P0,P1,P2,P3,其中P0是起点,坐标(0,0),P3是终点,坐标(1,1)
PI和P2才是最终生成速度曲线的关键
看了很多博客,没有一个讲解曲线变化怎么控制的,大部分都是列出了定义和常见的曲线,这对我并没有什么帮助,所以花了点时间玩了下
曲线结论(个人理解)
x轴
所占时间百分比
y轴
所占进程百分比(这里我理解为距离百分比,由你设置的时间,自动计算总距离)
分割线
P0与P3相连的直线

P1:红色 P2:绿色
P1与分割线产生的弧
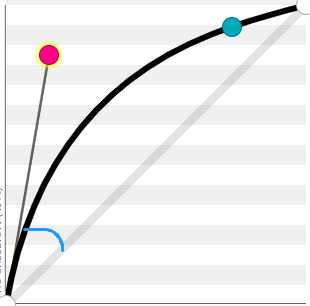
开始路线
上圆弧曲线
速度快
速度随着弧的角度越大越快,时间短(蓝色代表角度)
曲线变化:快-匀速-慢
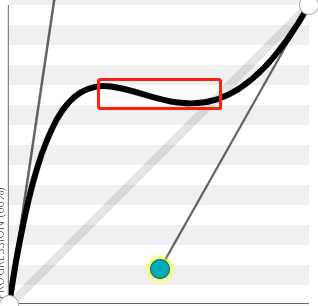
向上y轴大于1,出现反弹效果(红色高度代表反弹值)
曲线变化:快-反弹-慢
直线
匀速
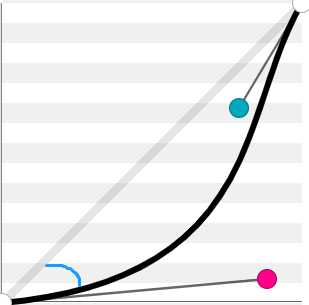
下圆弧曲线
速度慢
速度随着弧的角度越大越慢,时间长(蓝色代表角度)
曲线变化:慢-匀速-快
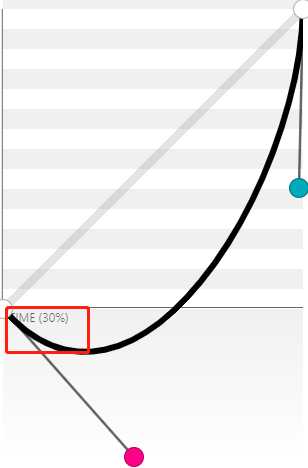
向下y轴小于1,出现反弹效果(红色高度代表反弹值)
曲线变化:反弹-匀速-快
P1和P2的过渡路线
P1和P2的弧相连会有一段距离
假设2s,每个点各分1s
p1的x1占用30%,剩70%,就是0.7s
p2的x2占用50%,剩50%,就是0.5s
距离滑动的时间就是1.2s,速度根据时间长短变化
曲线变化:慢-快-慢
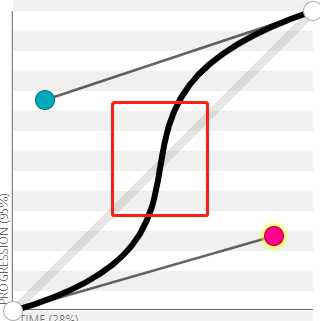
如果设置了反弹,距离就是反弹值,反弹时间1.2s
曲线变化:反弹-匀速-快
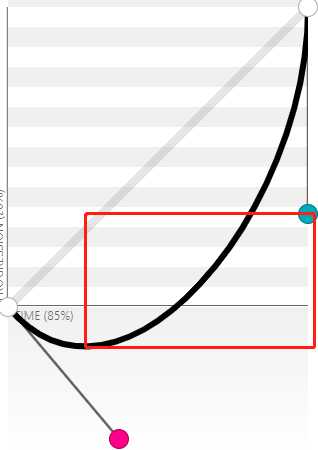
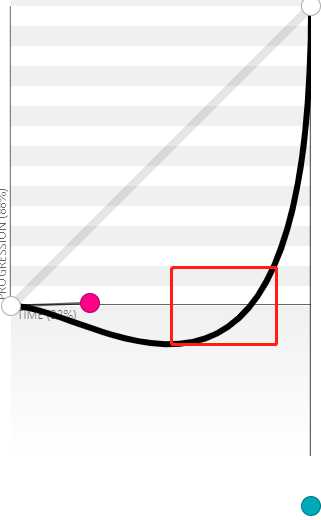
P2与分割线产生的弧
结束路线
上圆弧曲线
速度慢
速度随着弧的角度越大越慢,时间短(蓝色代表角度)
曲线变化:快-匀速-慢

向上y轴大于1,出现反弹效果
曲线变化:快-反弹
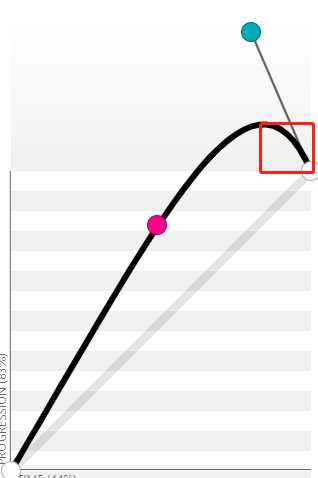
直线
匀速
下圆弧曲线
速度随着弧的角度越大越快,时间长
曲线变化:慢-匀速-快
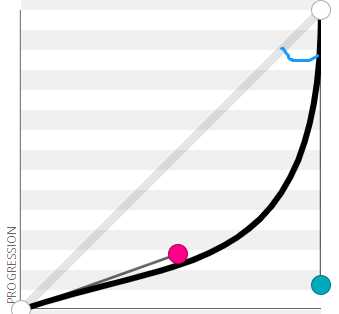
向下y轴小于1,出现反弹效果
曲线变化:反弹-匀速-快
以上就是我的理解,希望对你有帮助,如有好文章望推荐。
标签:定义 很多 idt ubi 变化 速度慢 怎么 假设 起点
原文地址:https://www.cnblogs.com/dongzhi1111/p/12115187.html