标签:str 精度 class atl grid diff mic matlab eps
这段代码实现了牛顿切线法、简化牛顿法和牛顿下山法这三种方程求解法,由于输出结果较长,只以牛顿下山法为例写一段例题
1.代码
%%牛顿迭代法
%%method为-1时为牛顿切线法,method为0时为简化牛顿法,method为1时为牛顿下山法
%%f是表达式f(x) = 0,X0是初值,epsilon是精度,interval是包含解的区间
function NM = Newton_method(f,X0,epsilon,interval,method)
Y0 = subs(f,X0);
%%作图
t = interval(1):(interval(2)-interval(1))/1000:interval(2);
T = subs(f,t);
T1 = zeros(1,max(size(t)));
Y1 = subs(f,X0)+subs(diff(f),X0)*(t-X0);
h = figure;
set(h,‘color‘,‘w‘);
plot(t,T,‘c‘,t,Y1,‘g‘,X0,Y0,‘ro‘,t,T1,‘y‘);
grid on;
xlabel(‘x shaft‘);ylabel(‘y shaft‘);
title(‘函数图像‘);
hold on
x(1) = X0;
ub = 100;e = floor(abs(log(epsilon)));
if method == -1
disp(‘牛顿切线法‘);
for i = 2:ub
x(i) = x(i-1)-subs(f,x(i-1))/subs(diff(f),x(i-1));
delta = x(i)-x(i-1);
if abs(delta) < epsilon
break;
end
end
disp(‘迭代次数为:‘);
i-1
disp(‘迭代解为:‘);
NM = vpa(x,e);
X_end = x(i);
Y_end = subs(f,X_end);
X = double([X0 X_end]);Y = double([Y0 Y_end]);
Y2 = Y_end+subs(diff(f),X_end)*(t-X_end);
plot(t,Y2,‘b‘,X_end,Y_end,‘mo‘);
legend(‘T:函数图像‘,‘Y1:初始点处切线‘,‘Y0:初始值处切点‘,‘T1:直线y=0‘,‘Y2:迭代解处的切线‘,‘Y_end:迭代解处切点‘);
for i = 1:2
text(X(i),Y(i),[‘(‘,num2str(X(i)),‘,‘,num2str(Y(i)),‘)‘],‘color‘,[0.02 0.79 0.99]);
end
elseif method == 0
disp(‘简化牛顿法‘);
for i = 2:ub
x(i) = x(i-1)-subs(f,x(i-1))/subs(diff(f),x(1));
delta = x(i)-x(i-1);
if abs(delta) < epsilon
break;
end
end
disp(‘迭代次数为:‘);
i-1
disp(‘迭代解为:‘);
NM = vpa(x,e);
X_end = x(i);
Y_end = subs(f,X_end);
X = double([X0 X_end]);Y = double([Y0 Y_end]);
Y2 = Y_end+subs(diff(f),X_end)*(t-X_end);
plot(t,Y2,‘b‘,X_end,Y_end,‘mo‘);
legend(‘T:函数图像‘,‘Y1:初始点处切线‘,‘Y0:初始值处切点‘,‘T1:直线y=0‘,‘Y2:迭代解处的切线‘,‘Y_end:迭代解处切点‘);
for i = 1:2
text(X(i),Y(i),[‘(‘,num2str(X(i)),‘,‘,num2str(Y(i)),‘)‘],‘color‘,[0.02 0.79 0.99]);
end
elseif method == 1
disp(‘牛顿下山法‘);
lambda = input(‘输入下山因子:‘);
for i = 2:ub
x(i) = x(i-1)-lambda*subs(f,x(i-1))/subs(diff(f),x(1));
delta = x(i)-x(i-1);
if abs(delta) < epsilon
break;
end
end
disp(‘迭代次数为:‘);
i-1
disp(‘迭代解为:‘);
NM = vpa(x,e);
X_end = x(i);
Y_end = subs(f,X_end);
X = double([X0 X_end]);Y = double([Y0 Y_end]);
Y2 = Y_end+subs(diff(f),X_end)*(t-X_end);
plot(t,Y2,‘b‘,X_end,Y_end,‘mo‘);
legend(‘T:函数图像‘,‘Y1:初始点处切线‘,‘Y0:初始值处切点‘,‘T1:直线y=0‘,‘Y2:迭代解处的切线‘,‘Y_end:迭代解处切点‘);
for i = 1:2
text(X(i),Y(i),[‘(‘,num2str(X(i)),‘,‘,num2str(Y(i)),‘)‘],‘color‘,[0.02 0.79 0.99]);
end
end
2.例子
clear all clc syms x; f = x^exp(x)-1; X0 = 0.8; epsilon=1e-6; interval = [0,2]; method = 1; %%牛顿下山法 X = Newton_method(f,X0,epsilon,interval,method)
结果如下
牛顿下山法
输入下山因子:0.8
迭代次数为:
ans =
21
迭代解为:
X =
[ 0.8, 1.025142203855, 0.9839179688712, 1.008330092139, 0.995101056432, 1.002691649998, 0.9984619264687, 1.000859946529, 0.99951321039, 1.000273650001, 0.9998455622605, 1.000086966616, 0.9999509665425, 1.000027626624, 0.9999844283422, 1.000008774959, 0.9999950545033, 1.000002787045, 0.9999984292923, 1.000000885191, 0.9999995011337, 1.000000281144]
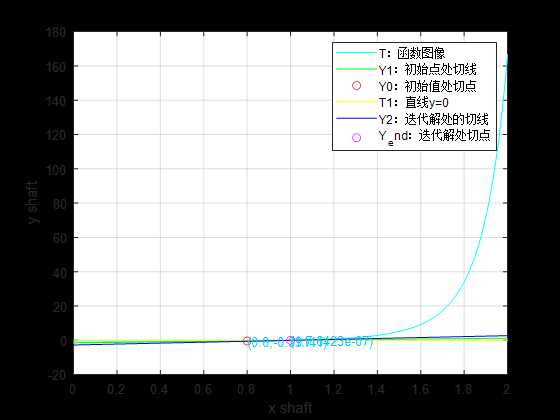
由于迭代函数原因,图象上的数据显示出现了遮挡,这一部分的代码以后再进行优化
标签:str 精度 class atl grid diff mic matlab eps
原文地址:https://www.cnblogs.com/guliangt/p/12119173.html