方程求根——两种加速迭代法

%%注意，这里的fei不再是形如f(x)=0的形式而是x=fei(x)的形式，有些fei(x)不收敛，需要寻找，X0是初始值，method取值0和1代表上述两种方法
function AIM = Accelerated_iteration_method(fei,X0,epsilon,method)

%%作图
t = X0/2:X0/1000:2*X0;
T = subs(fei,t);
y0 = t;
h=figure;
set(h,‘color‘,‘w‘);
plot(t,T,‘r‘,t,y0,‘b‘);
grid on
legend(‘T：函数图像‘);
xlabel(‘x shaft‘);ylabel(‘y shaft‘);
title(‘函数图像‘);
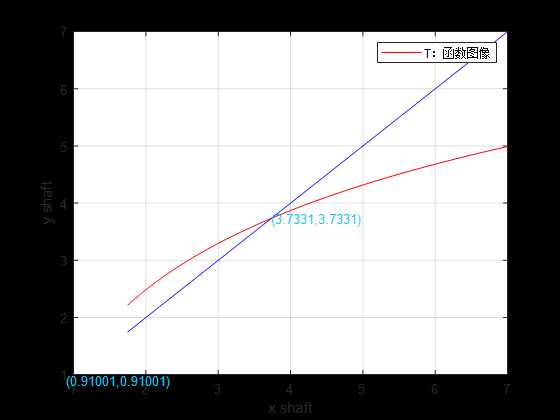
disp(‘图像中两函数交点为 x = fei(x) 的解‘);
syms x;
X_real = double(solve([fei-x],[0]));
for i = 1:max(size(X_real))
    if isreal(X_real(i)) == 1
        x_real(i) = X_real(i);
    else 
        x_real(i) =0;
    end
end
x_real(x_real==0)=[];
for i = 1:max(size(x_real))
    text(x_real(i),x_real(i),[‘(‘,num2str(x_real(i)),‘,‘,num2str(x_real(i)),‘)‘],‘color‘,[0.02 0.79 0.99]);
end


e = floor(abs(log(epsilon)));
if method == 0
    disp(‘此算法为埃特金加速迭代法‘);
    X1 = subs(fei,X0);X2 = subs(fei,X1);
    ub = 100;
    X(1) = X0;X(2) = X1;X(3) = X2;
    for i = 1:ub
        X_ba(i) = X(i) - (X(i+1)-X(i))^2/(X(i)-2*X(i+1)+X(i+2));
        X(i+3) = X_ba(i);
        delta = X(i+3)-X(i+2);
        if abs(delta) < epsilon
            break;
        end
    end
    disp(‘迭代次数为：‘);
    i
    disp(‘Xba，X分别为：‘);
    AIM = vpa([0 0 0 X_ba;X],e);
elseif method == 1
    disp(‘此算法为斯特芬森加速迭代法‘);
    ub = 100;
    X(1) = X0;
    for i = 1:ub
        Y(i) = subs(fei,X(i));
        Z(i) = subs(fei,Y(i));
        X(i+1) = X(i)-(Y(i)-Z(i))^2/(Z(i)-2*Y(i)+X(i));
        delta = X(i+1)-X(i);
        if abs(delta) < epsilon
            break;
        end
    end
    disp(‘迭代次数为：‘);
    i
    disp(‘X,Y,Z分别为：‘);
    AIM = vpa([X;0 Y;0 Z],e);
end
end

clear all
clc
syms x;
fei =log(x)+log(5);
epsilon=1e-6;
X0 = 0.5;
method = 1;

%%斯特芬森加速迭代法
Z = Accelerated_iteration_method(fei,X0,epsilon,method)

图像中两函数交点为 x = fei(x) 的解
此算法为斯特芬森加速迭代法
迭代次数为：
i =
    34
X,Y,Z分别为：
Z =
[ 3.5, 3.575575323263, 3.624589351868, 3.657490016934,  3.68002713941, 3.695664194037, 3.706605521034, 3.714304871981, 3.719744047836,  3.72359695842, 3.726331398288, 3.728274642564, 3.729656921924, 3.730640829335, 3.731341507244,  3.73184065469, 3.732196321463,   3.7324497945,  3.73263045906, 3.732759240038, 3.732851043115,  3.73291648892, 3.732963146263, 3.732996409757,  3.73302012473, 3.733037032344, 3.733049086743, 3.733057681058, 3.733063808493, 3.733068177146, 3.733071291853, 3.733073512541, 3.733075095823, 3.733076224655, 3.733077029479]
>>