标签:计算 时间 试验 提高 分析 而且 失效 特性 可靠性
在硬 件可靠性 理 论 中 , 典 型 的失效 率 又( t ) 函 数是 一条 形 似“ 浴 盆” 的曲线 。 浴 盆 曲线 由三 段 构成 : 早 期故 障期 、 偶 然故 障期 、 耗损 故 障期 。 这种 曲线描 述 了事物 生命期 的 整个过 程 , 而 且具 有普遍 性 。 对 软件来 说 , 在调 试排错 阶 段 , 故 障易 被发现 , 也 易于 纠正 , 而且 在纠 正 中引 人新 故 障的概率 较小 , 因此 , 在 此 阶段 , 软件 失效率 是递 减 的 ; 当软件 中存在 的残 留错误 数减 少 到一 定数 目后 , 由于 故 障发 现率 较 低 , 故 障机 理 较复 杂 , 再 发现 的错 误 一 般就 难 以 得 到 纠 正 , 甚至 在纠正 过 程 中又 引人新 的错误 , 从 而使 得 软件 在运 行 阶 段失 效 率基 本保 持 不变 ; 在 软件 生存 的后期 , 由于 软件 应用 范 围 的扩 大 , 或 用 户对 软件 功 能 提 出更 新 的要求 , 从 而 导致 软件故 障增多 , 而 对其 纠 正越来 越 困 难 , 很 易引入新故 障 , 这样 使 得软件 失效 率呈 递增趋 势 , 直到软件寿命 期结 束 。 因 此 , 人 们把 浴盆 曲线 理论运 用到 软件 可 靠性领 域来 , 结合 软件 固 有 特性 , 提 出了许 多评 估软 件 可 靠性 的模 型 , 并 在实 践 中 得到 了广 泛 应用 , 取 得 了 良好 效 果 。
J一M 模型 就是 其 中 的一 种 , 它对 应 于浴 盆 曲 线 的第一 段 , 适 用 于软 件 调 试排 错 阶 段 , 这类 模 型 统称 为软件 出生 模型 ( Born-In模型)。
J 一M 模型 是 由 2 . Je lin s ki 和 P . B . M o r a n d a 于 19 7 2 年提 出的一种 确定 性模 型 , 简 称 J一 M 模型 , 用来描述 软件 错误 的检 测过 程 。 根据软件 特性 , 在 B o r n 一 n I 模 型 中规 定 了 四 条基本 假设 :
J一M 模 型 除 上述 四 条基 本假 设外 , 还增 加两 条假设 :
由上 述假设 可 得到 J一M 模 型 的失 效率 曲线 如 图 所示 :
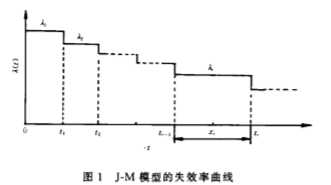
失 效率 和 可靠 度 函 数 可 表示 为 :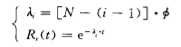
式 中 , N 表 示 开始 时 软 件 存 在 的 错 误 总 数 ; ∮表 示错 误 尺 寸 , 由假设 6 知∮是 个 常数 ; λ表示第( i一 1 ) 次 失 效 至 第 i 次 失 效 为止 , 这 段时 间 的失效 率 ; Ri ( t )表 示第( i 一 l ) 次失 效 至第 i 次失 效 为止 , 这段 时 间的软 件可靠性 函 数 。
式 中的 N 、 ∮必两参 数可 由极 大 似然法 估计 出来 。 如果 以 X i ( i=1 , 2 , … , n ) 表示被 观察 到 的一 系 列失 效 间 隔时 间 , 则 可 求 得第 n 次失 效后 的软件 可 靠性 函 数 估 计 , 以 及到 第 n + 1 次 失效 发生 的平均 间隔 时间 的估 计 。
J一M 模 型 的准确性 主要 取 决于 假设 的有效 性 。 在 软件 的调试排 错 阶段 , B o r n 一玩 模 型 的 四 个基 本假 设 是 比 较 合理 的 , 而 对于 J一M 模 型 所 附 加 的 两条 假设 , 在 软 件 工 程实 践 中具 有 一 定的缺 陷 。 首先 , 软件 的失效 率不 仅仅 取决 于 当前残 留错 误数 。 例如 , 一个 仅含 有 两个不 常碰到 的 错 误 ( 即错 误 尺 寸非 常小 , 如 0 5 死锁 等 ) 的 软件 5 1 , 另 一个 仅 含有 一个 经 常 出现 的错 误 ( 即 错误尺 寸较大 , 如 下标动 态超 界等 ) 的软件 5 2 。 显而 易见 S , 比 S : 可靠性 高 。 这样 , 假 设 5 就 不 成 立 。 其次 , 根 据 定义 , 错 误尺 寸是 某一 错误 导致 软件 失效 的概率 , 即对 软件 失效 率 的贡 献率 。 很 明显 , 错误 尺 寸越大 , 就越 容易 造成 软件 运行 失效 , 就越 容易被 发现 ; 反 之 , 错 误尺 寸越小 , 就越难 被发现 。 从 另一 角度说 , 越 先 发现 的错误 , 其错 误尺 寸越大 ; 而越 是 后发 现的错 误 , 其 错 误尺 寸越小 。 也 就是说 , 不 同的 软件 错误 , 其错 误尺 寸是 不相等 的 , 而是 随着被 发现 的顺 序 呈 递减 序列 。 这样 , 假设 6 也 不成 立 。 综 上 所述 , J一 M 模型 所 附加 的 两 条 假 设 , 对于 某 些 软 件 工程不 适 用 , 不 能很 好地 反映 软 件 的客观状 况 。 此外 , 适 用于 软 件 调试 阶段 的其它 出生模 型 , 如 B a y e S 模 型 、 Sh o o m a n 模 型 、 非 出错计数 模 型 等 , 也都存 在 类似 的 问题 , 为此 , 应 予改 进 。
软件 的失效 率不 仅与其 残 留错误 数 有关 , 而 且与每 个错 误 的错 误尺 寸有 关 。 如 果软件 残设 : 开始 时软件 的残 留错误 数 为 N , 其 相 应 的错 误尺 寸 为 ∮j( j= 1, 2 , … , N ) , 则 失 效 率与可靠性 函 数 由下 式表 示 :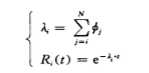
由于 错误 尺 寸随 着发现 的先后 次 序呈 递减 序列 , 因此 : ∮j>∮j+1; 。 如果 直接 用 ( 2 ) 式 进行分 析计算 , 比较 困难 。 为减化计算 , 根据 ( 3 ) 式 引人假 设 7;
假设 7 : 第 i ( + l ) 个 错 误 与 第 i 个 错 误 的 错 误 尺 寸 之 比 为 常 数 。 即 : ∮j+1=K*∮j( 0 < K < 1 )。
令 笋 ∮j=∮1 ,则,∮j=kj-1* ∮这样 ( 2 ) 式变 为 :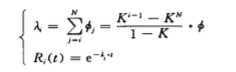

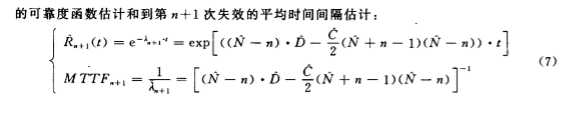
软件 测试 数据 是 软件 可靠性 评估 的基础 , 在软 件调 试排错 阶段 , 开 发人 员应详细记 录每 次 软件故 障 间隔 时间 , 保证 数据 的客 观性 和 准确性 。 对 收集 的数据 在用 于评估 前 , 应进 行初 步处 理 。 对重 复 出现 的故 障 , 应将 前 几 次故 障数据 剔除 , 保 留最后一 次真 正 消除软 件故 障的 那个数 据 , 即如 果第 i 次 出现 的故 障剔 除 不成 功 , 应将 x ` 删 除 , 同时 将 x 、 ,数 据 赋 予 x 、 , 即 : x 、 一` + , 一 t、 , 以 此 类 推 。 另外 , 如果 有 多个 程 序模 块 , 则 各模 块 的故 障数 据应 分别 记 录 , 不 要 混 淆 , 同一程 序模 块 的不 同版本 的软 件故 障数 据也 不要混 淆 。 收集到 一定 数量 的数 据后 , 就 可 以 进行 数据 分析 , 代 入评估模型 进 行评估 。
5 结束语
过 去 由于缺 少切 合 软件 开发 实际 的 软件 可靠 性评估 模 型 , 在 系统 工程 产 品 的可 靠性 分 析 和评估 中 , 只 对 硬件进 行 , 而将软 件 可靠 度视 为 1 , 即不 考虑软件 可靠 性 问题 。 事 实上 随着 硬件 可靠性 的不断 提高 , 软件 可靠性 显 得 日益突 出 。 而 且一 个软件 模块 , 开发 人员 调试到 什 么 程 度就 可结 束调 试排错 , 也 就是 如何 确定 软件 调试周 期也 是个 棘手 的问题 。 本文 正是基 于 这 种 情况 , 结 合 系统 工程 实 际 , 对 软件 调试 排错 阶段 的可 靠性 评估 模 型 进 行探 索 , 使 得软 件 开发 人员在 软件 调试 阶段 收集 n 个 数据 后 , 经 过 预处理 , 运 用本 文提供 的评估 模型 计算得 到 该 软件 残 留错 误总数 及下 一个 软件故 障出现 的平 均时 间 。 排除第 n 个软 件错 误后 , 也可 以估 计 出该软件 的平 均无 故障 时 间及 排 除剩 余软件 错 误还需 工作 的时 间 。 这 对于 开展 软件可 靠 性 增 长试验 , 合理 确定 调试 周期 , 调整 软件 开发 计划等有 较大 作用 。
标签:计算 时间 试验 提高 分析 而且 失效 特性 可靠性
原文地址:https://www.cnblogs.com/yilang/p/12121022.html