标签:最大值 曲线 表示 个人 分析 margin 苹果 世纪 width
1、效用(utility):消费者在消费商品或服务时所感受到的满足。
三个特点:
效用理论的基本假设
1、完全信息
2、偏好次序
基数效用与序数效用
1、基数效用论(使用边际效用分析法)
基数效用论:形成于19世纪。效用是一个数量概念。认为,一种商品或劳务效用的大小,可以用基数(1,2,3· · ·)测量。衡量单位是效用单位(Util,尤特尔)。
例如:吃一个面包得到的满足是4 Utils,看一场电影的满足是8 Utils。
2、序数效用论(使用无差异曲线分析法)
序数效用论:产生于20世纪30年代。效用是一个次序概念。认为,效用的绝对量大小根本无法测定,无法用某种统一的单位表示出来,它们只能根据消费者的个人偏好程度排列出效用大小先后的顺序。
例如:阿珂在苹果和桃子中,选择了苹果,放弃了桃子。则对我而言,苹果的效用大于桃子。或者说苹果效用第一(最大),桃子效用第二(次之)。
1、总效用与边际效用
总效用(TU):指消费者在一定时期内从一定数量的商品消费中获得的效用量的总和。
边际效用(MU) :指消费者在一定时间内增加一单位商品的消费时,所获得的总效用量的增量。(例如我吃第一个包子获得10u,第二个包子18u。边际效用=18-10=8u)
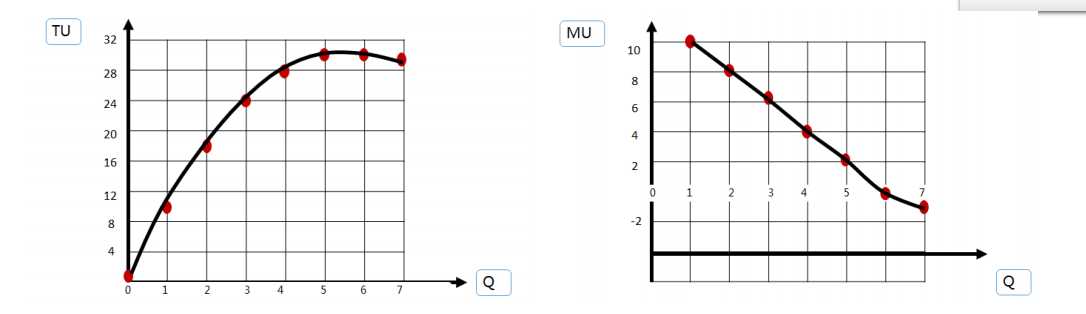
当MU>0时,总效用曲线呈上升趋势。表明总效用会随着消费量的增加而增加 ,但增加的幅度是递减的。
当MU=0时,总效用曲线达到最高点,表明总效用取得最大值。这种情形意味 着消费者从该商品的消费中所能够得到的一切可能的满足都得到了。
当MU<0时,总效用曲线呈下降趋势,表明总效用随着消费量的增加而减少。
边际效用递减规律:随着消费数量增加,边际效用呈下降趋势的现象。 某一种商品的边际效用大小,主要取决于商品消费量的大小。
2、消费者均衡
消费者均衡:研究单个消费者如何把有限的货币收入分配在对各种商品的贩买中获 得效用的最大化。

均衡条件的含义:消费者使自己花费在各种商品贩买上的最后一元钱带来的 边际效用相等,也称等边际效用原则。

2、消费者剩余
消费者剩余:消费者愿意为某一商品支付的价格不在贩买该商品时实际支付的价格之间的差额
在序数效用论中,效用函数不代表效用水平,不代表具体数值,只代表先后顺序。 序数效用论用无差异曲线分析法来说明消费者均衡的实现
1、无差异曲线
无差异曲线:表示消费者偏好相同的两种商品的不同数量的各种组合。同一条无差异曲线是表示两种商品的不同数量的组合对消费者所提供的效用 是相同的
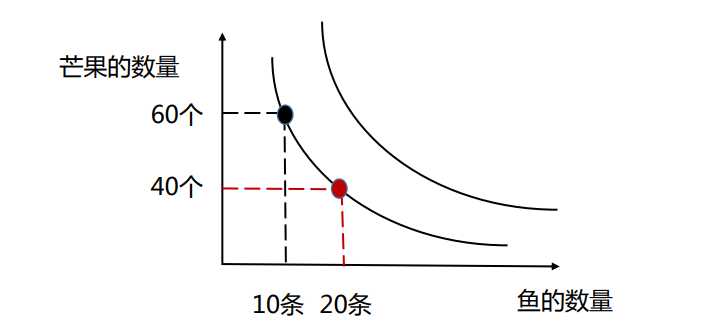
无差异曲线的性质:
2、边际替代率(MRS)
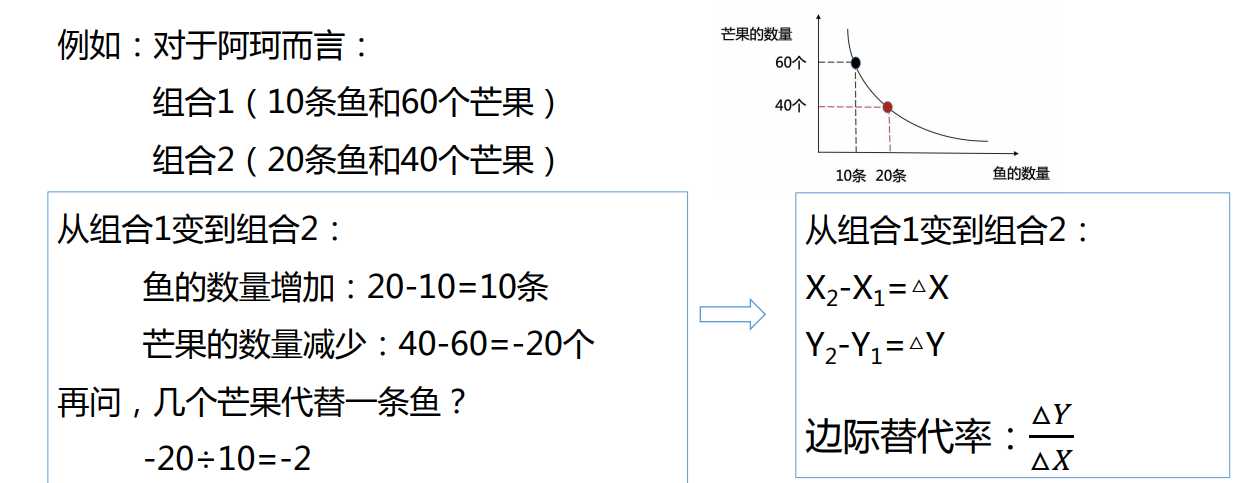
1、边际替代率(Marginal Rate of Substitution,MRS) :消费者在保持自己效用水平不变的情况下,为了增加一种商品(X)的消费量所愿意放弃的另一种商品(Y)的消费量。

3、消费者的预算线
预算线(budget line):给定的价格和收入下,消费者把所有收入用于消费所能获 得的商品组合点的轨迹。

4、消费者均衡
消费者均衡:在预算给定的情况下,消费者通过决定两种商品的消费量使得自己 的效用最大化的状态。

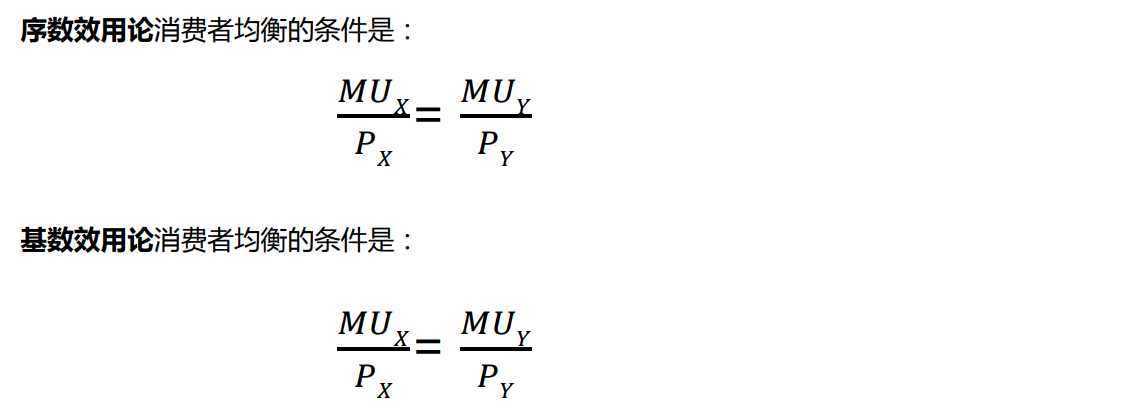
=============================数学知识================================
1、数据知识求导:
数学中有一个方便的方法,叫做求导,用来解决经济学中边际的问题。
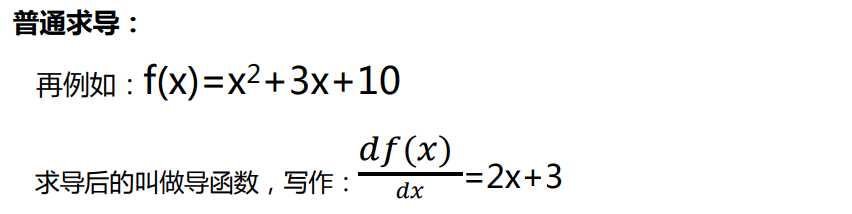

2、偏分求导。效用函数为U=XY。求X和Y的边际效用。

标签:最大值 曲线 表示 个人 分析 margin 苹果 世纪 width
原文地址:https://www.cnblogs.com/jalja/p/12121868.html