标签:就是 度量 str 最小 之间 info span 分类 计算
谱聚类是基于谱图理论基础上的一种聚类方法,与传统的聚类方法相比:
具有在任意形状的样本空间上聚类并且收敛于全局最优解的优点。
通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,从而达到对样本数据进行聚类的目的;
其本质是将聚类问题转换为图的最优划分问题,是一种点对聚类算法。
谱聚类算法将数据集中的每个对象看做图的顶点V,将顶点间的相似度量化为相应顶点连接边E的权值w,这样就构成了一-个基于相似度的无向加权图G(V,E),于是聚类问题就转换为图的划分问题。
基于图的最优划分规则就是子图内的相似度最大,子图间的相似度最小。其中,V代表所有样本的集合,E代表权重的集合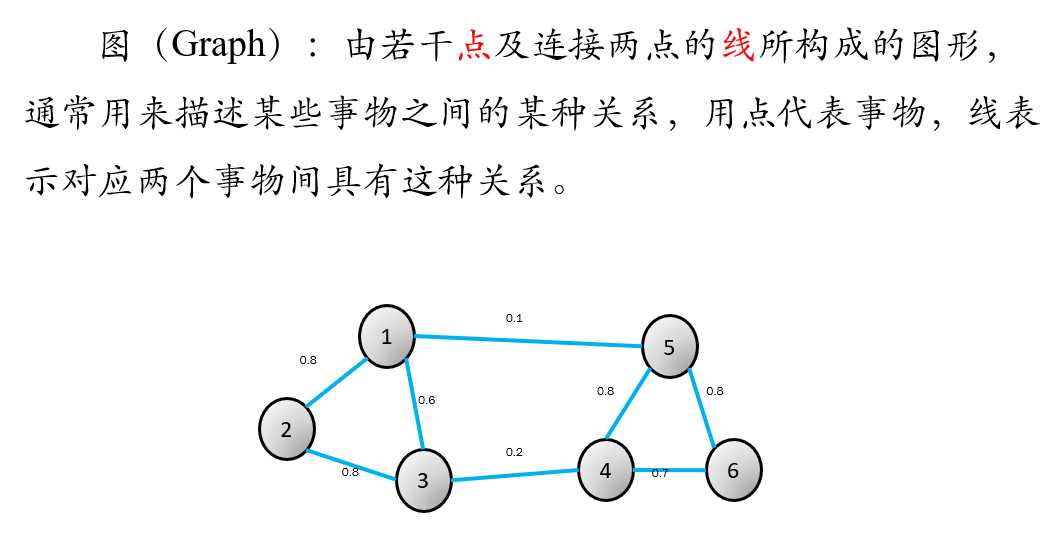
在这图里面,样本即是123456,他们之间的相似度量化为了权重
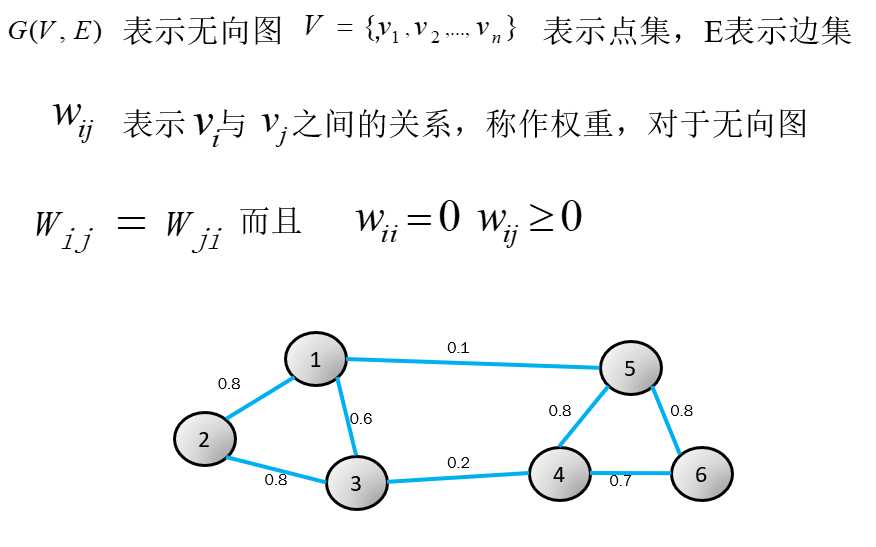
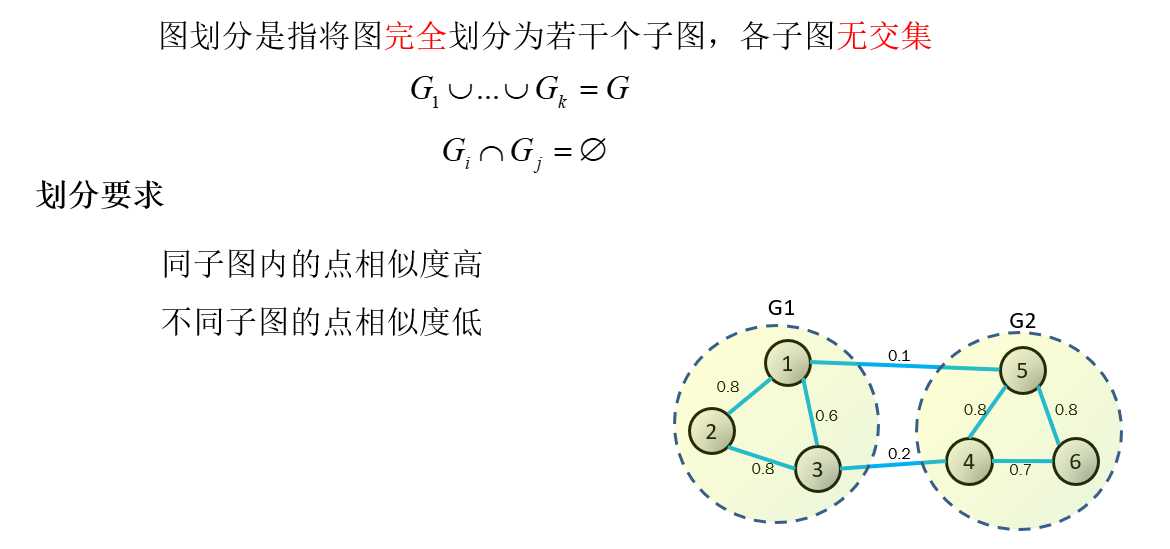
损失函数为1与5,3与4之间的权重
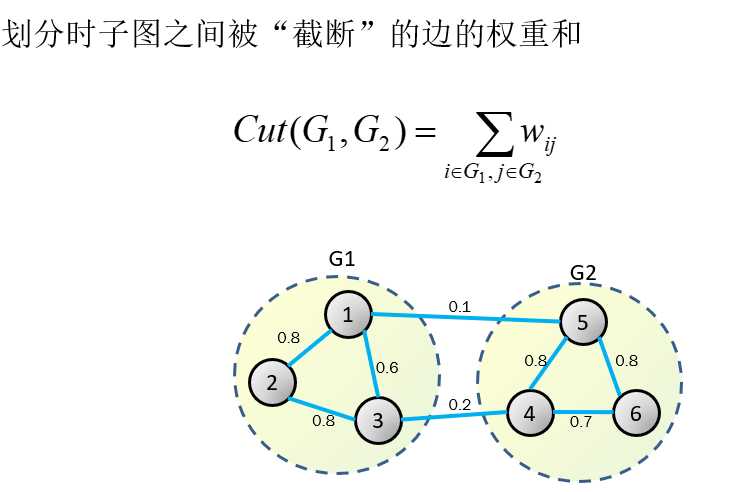



说实话,这么乱,我也懵,举个大栗子!
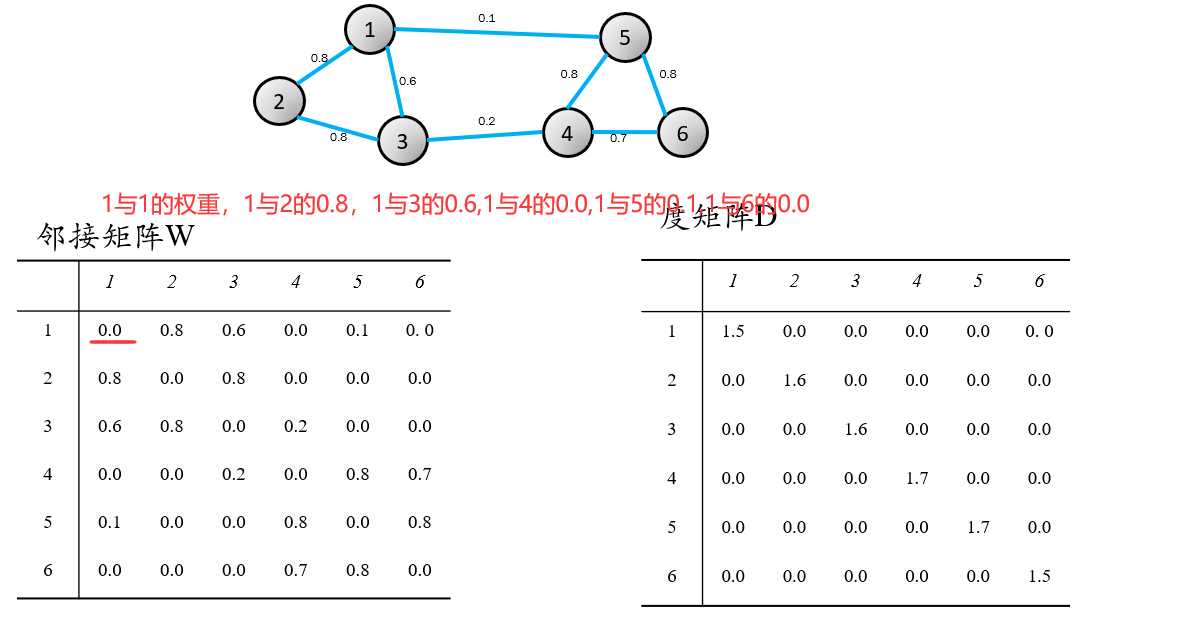
度矩阵就是邻接矩阵每一行的和放到对应的第(第几行)个位置。
L=D-W.
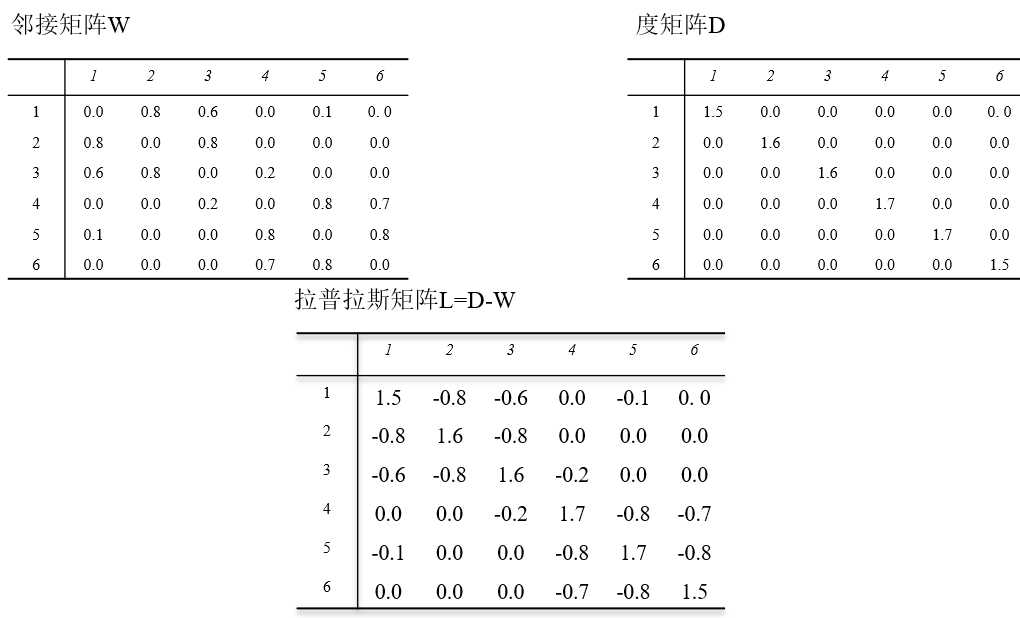



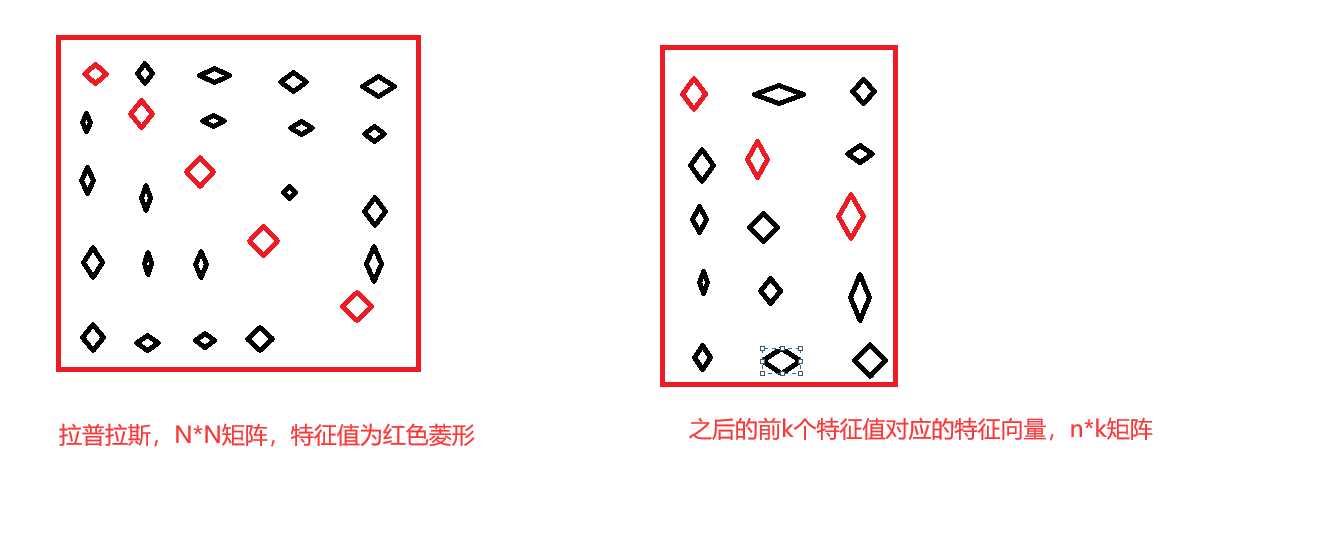
LX=λX,L是拉普拉斯矩阵,代表着关联程度。λ是特征值,第三步计算出特征值后,将特征值从小到大排序(因为特征值越小,关联程度越小,越容易划分类别,也就越容易聚类),将特征向量作为新的特征属性描述数据集,,画图丑了点,各位看官老爷将就看哈


标签:就是 度量 str 最小 之间 info span 分类 计算
原文地址:https://www.cnblogs.com/qianchaomoon/p/12129656.html