标签:矩阵 怎么 解决 识别 等价 拉格朗日乘子 应该 最好 使用
对于分类问题,还有一种算法叫做支持向量机SVM,我们简化一下二分类数据,假设这些数据只有二维特征,其数据如下:
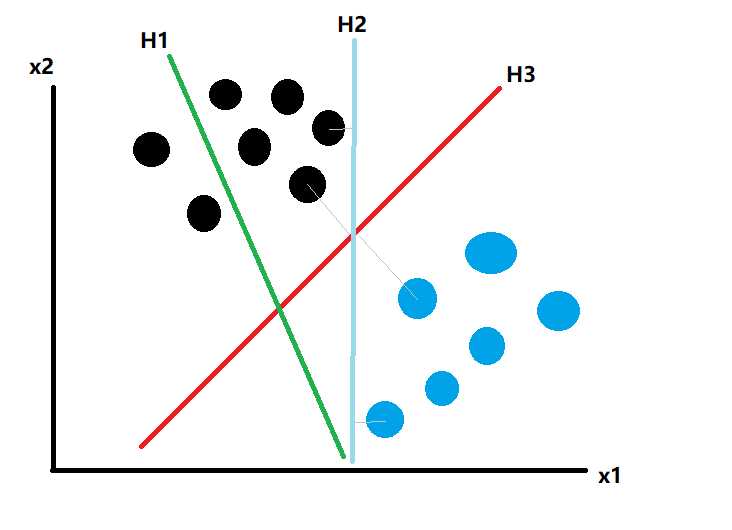
我们希望找到一条线,把这些数据能够分类识别,图中三条线,H1是失败的,H2和H3都可以正确分类,但是明显肉眼可以识别出,H3要比H2更好,对于新的未知数据其准确度也是更高的,它们却别在于两类数据集中,距离分割线最近点离分割线的距离,H3要比H2更大(灰色四条法线)。所以在对新的数据进行分类,H3要比H2更准确。推广到N维特征向量和分类超平面,各类数据中距离分类超平面最近的点(向量)就是支持向量。当我们调整超平面的方程时,使得支持向量与超平面的距离最大化。就得到最优分类超平面。这就是支持向量机SVM的算法。
SVM怎么得到分类超平面?让我们接着往下看:
给定样本集
\[
D=(x_1
?
,y_1
?
),(x_2
?
,y_2
?
),...,(x_m
?
,y_m
?
))),y
i
?
∈\{?1,1\}
\]
? 对于$ y∈{?1,1}$,当然不会只是认为y只能是-1或1.如果y=2000表示正向,或y=0表示反向,y=300表示正向,或y=5是正向。y只是一个标签,标注为{-1,1},方便描述,所以
\[
w^Tx_i + b ? +1,y_i = +1
\]
\[ w^Tx_i + b < -1,y_i = -1 \]
线性分类器基于驯良样本D再二维空间找到一个超平面分来二类样本,当然这样超平面由很多:
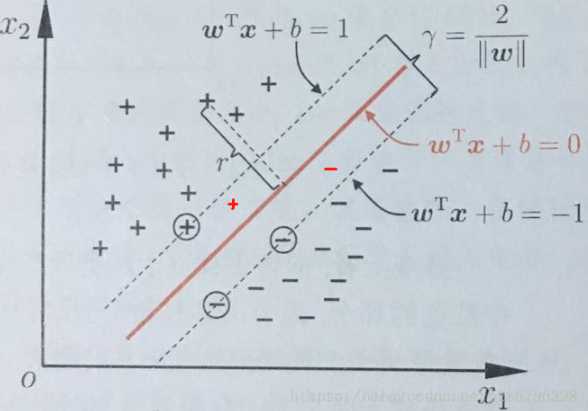
注意:\(||w||\)为范数,用来度量某个向量空间(或矩阵)中的每个向量的长度或大小
由上图,这根红线代表超平面抗扰动性最好,这个超平面离支线两边数据的间隔最大,对训练集的数据巨行星或噪声最大容忍能力。
? 这个超平面用如下函数表示
\[
f(x)=w^Tx+b
\]
? 当\(f(x)\)等于0时候,x便是位于超平面点上。而\(f(x)\)大于0点对应y=1的数据点,\(f(x)\)小于0的点对应y=-1的点。
? 所谓支持向量,使得\(w^Tx_i + b\)大于+1或小于-1就更加支持样本分类。为什么要这么搞:
? 我们可以计算得到空间中任意样本到点\(x\)超平面的距离为:$r = \frac{w^Tx+b}{||w||} $,如下图:
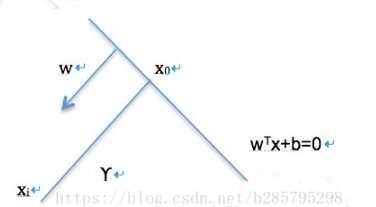
? 有:\(x = x_0 + r\frac{w}{||w||}\)(简单平面集合),因为\(x_0\)在超平面上,\(f(x_0)=0\),也就是\(w^Tx_0+b=0\),代入上式,可以得到:\(r = \frac{w^Tx+b}{||w||}=\frac{f(x)}{||w||}\),为了得到r的绝对值,令r乘上对应的类别y.就可得出几何间隔\(r=yr=\frac{r}{||w||}\)。从上面可以看出,几何间隔除以\(||w||\)才是直观超平面的距离。
? 因\(y∈\{?1,1\}\),超平面上下支持向量到超平面距离都为1,则它们间隔为\(r=\frac{2}{||w||}\)
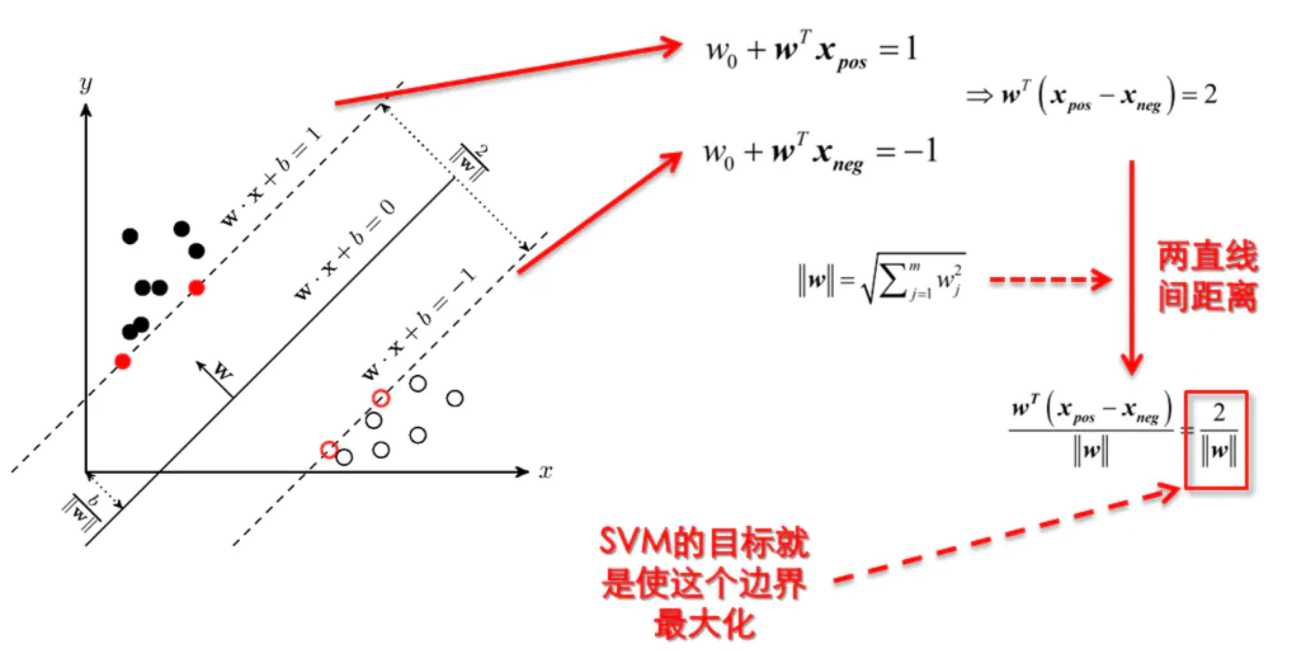
? 对于分类,我们已经假设\(y∈\{?1,1\}\)。那么
\[
w^T
x_i
?
+b?0,时,对应y_i
?
取正例,表示为y_i
?
=+1;
\]
\[ w^T x_i ? +b<0,时,对应y_i ? 取负例,表示为y_i ? =-1; \]
? 则SVM最大分类间隔为max margin,因为我们前面定义\(w^T x_i+b?0,时,对应y_i 取正.w^Tx_i+b<0时,对应y_i取负\)。
(margin是直线距离,每一类样本中所有样本点到直线的距离为):
\(\frac{w^Tx+b}{||w||}\)
? 单侧margin应该是每一类样本中到超平面最近点与超平面的距离(支持向量到超平面距离)那么margin等于2倍单侧margin。两个支持向量距离,如下:
\[
margin = 2× \min_{w,b,x_i}\frac{w^Tx_i+b}{||w||},i = 1,...,m
\]
? 回到我们之前假设,我们有\(y_i(w^Tx_i+b)?0\),则有:
\[
margin = 2× \min_{w,b,x_i}\frac{w^Tx_i+b}{||w||}=2× \min_{w,b,x_i,y_i}\frac{w^Tx_i+b}{||w||},i = 1,...,m
\]
? 消除分子中绝对值则有:
\[
\max_{w,b}\frac{2}{||w||}?\min_{x_i,y_i}y_i(w^Tx_i+b),s.t.y_i(w^Tx_i+b)?0,i = 1,...,m
\]
? 当\(y_i(w^Tx_i+b)?0,i = 1,...,m\)存在任意值a大于0,使得\(\min_{x_i,y_i}y_i(w^Tx_i+b)=a\),
? 我们使a=1,简化运算那么得到:\(\min_{x_i,y_i}y_i(w^Tx_i+b)=1\)
? 于是SVM目标进一步变为:
\[
\max_{w,b}\frac{2}{||w||},s.t.y_i(w^Tx_i+b>1,i=1,...,m)
\]
? 由于求\(max\frac{2}{||w||}\)的最大值相当于求\(min\frac{1}{2}||w||^2\)的最小值, 所以上述目标函数等价于 (w由分母变为分子,所以从max变为min):
\[
min\frac{1}{2}||w||^2 ,s.t.y_i(w^Tx_i+b)≥1,i=1,...,m(公式1)
\]
? 因此现在目标函数是二次,约束条件是线性的,是凸二次规划问题。由于问题特殊结构通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
? 那什么是拉格朗日对偶性呢?简单来讲,通过给每一个约束条件加上一个拉格朗日乘子(Lagrange multiplier)\(a\),定义拉格朗日函数(通过拉格朗日函数将约束条件融合到目标函数里去,从而只用一个函数表达式便能清楚的表达出我们的问题):
? 比如对公式1每一个约束(共有m个约束,\(y_i(w^Tx_i+b)>1\)),添加拉格朗日乘子\(a_i≥0\),则整个问题函数可表示为:
\[
L(w,b,a) = \frac{1}{2}||w||^2 + \Sigma^m_{i=1}a^i(1-y_i(w^Tx_i+b)) (公式2)
\]
? 然后我们令:
\[
\Theta(w) = \max_{a_i≥0}L(w,b,a)
\]
? 为何使用这样拉格朗日乘子,又为何这样构建?我们目标函数是不等式约束,解决二次规划问题,我们选择用KKT条件,而KKT条件需要这样一个约束\(a_i≥0\).最终我们通过KKT条件来产生原问题对偶问题。
? 可以看到由于\(a_i≥0\),这样,单反又约束条件值一不满足,如\(y_k(w^Tx_k+b)<1\),那么显然\(\Theta(w) =∞\)(只要令\(a_i=∞\)即可)而当所有约束条件均满足时,$\Theta(w) \(最优解为\)\frac{1}{2}||w||^2\(,所以\)\frac{1}{2}||w||^2\(等价于最小化\)\Theta(w) \(,当然必须满足约束条件\)a_i≥0,i=1,...,n\(,因为如果约束条件没有得到满足\)\Theta(w) $会等于无穷大, 也不会得到最小值。机题函数如下:
\[
\min_{w,b}\Theta(w) = \min_{w,b}\max_{a_i≥0}L(w,b,a) = p^*
\]
? 这里用\(p^*\)表示最优值,那么首先需要面对\(w\),\(b\)两个参数,而\(a_i\)又是不等约束,这个求解过程过于复杂不容易做,不如把最小和最大位置交换一下如下:
\[
\max_{a_i≥0}\min_{w,b}L(w,b,a) =d^*
\]
? 交换以后的新问题是原始问题的对偶问题,这个新问题最优值用\(d*\)来表示,并且有\(d^*≤p^*\),在满足某县条件下,这两者之间相等。此时可以求解对偶问题来间接地求解原始问题。(之所以从minmax的原始问题\(p^*\)转换成maxmin对偶问题\(d^*\),一是因为\(d^*\)是\(p^*\)的近似解,二是转化为对偶问题后,更容易求解)。下面可以先求\(L\)对\(w\),\(d\)的极小值,再求\(L\)对\(a\)的极大值。
(如果对对偶问题不是很理解可以点此一个简单案例,能让你更好理解对偶问题)
? 上述中存在着\(d^*≤p^*\)情况下,两者是等价。所谓"存在着"就是要满足KTT条件
? 一个最优化数学模型能够表示成下列形式:
\[
min f(x) \\ s.t. h_j(x)=0,j=1,...p.\\g_k(x)≤0,k=1,...,q,\\x∈X?R^n
\]
? 由上式可以看出\(f(x)\)式最小化的函数,\(h(x)\)式等式约束,\(g(x)\)式不等式约束,\(p\)和\(q\)分别为等式约束和不等式约束。
?
同时需要明白:
? 凸优化的概念: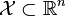 为一凸集,
为一凸集, 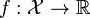 为一凸函数。凸优化就是要找出一点
为一凸函数。凸优化就是要找出一点 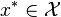 ,使得每一
,使得每一  满足
满足 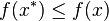 。
。
? KKT条件的意义:它是一个非线性规划(Nonlinear Programming)问题能有最优化解法的必要和充分条件。
? 于是最优化数学模型最优解必须满足条件如下:
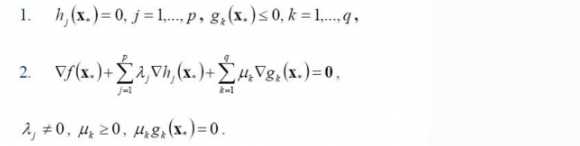
未完待续。。。
原文链接参考:
标签:矩阵 怎么 解决 识别 等价 拉格朗日乘子 应该 最好 使用
原文地址:https://www.cnblogs.com/xujunkai/p/12129455.html