标签：域名   文件   eal   actor   开关   语句   printf   while语句   离散   

Matlab复习提纲

一、概述

1. Matlab（Matrix Laboratory）概述

• 1980年，由美国的 Clever Moler 博士开发；
• 是一款 科学与工程计算软件；
• 第四代智能计算机语言。

2. 功能与特点

• 开放性强、可扩展性强，兼容性强，直观灵活；

• MATLAB提供了丰富的矩阵运算处理功能，是基于矩阵运算的处理工具；

• 矩阵运算：

  B = A'            %矩阵转置
  B = A + 1     %矩阵加法
  B = A * 3     %矩阵乘法
  C = flipud(B) %矩阵上下翻转
  C = rot90(B)  %矩阵逆时针旋转90°

• 数组操作

  %MATLAB中所有数据类型的所有变量都是多维数组。向量是一维数组，矩阵是二维数组。
  %下面这些函数，单个参数创建一个正方形数组，双参数创建矩形数组。
  zeros()   %全0
  ones()    %全1
  eye() %单位矩阵
  rand()    %在(0,1)上创建均匀分布的随机数的数组
  randn()   %产生正态分布随机数组
  diag()    %产生对角型数组
  size()    %返回指定矩阵的行数和列数
  magic() %魔方矩阵（魔方矩阵又称幻方，是有相同的行数和列数，并在每行每列、对角线上的和都相等的矩阵。魔方矩阵中的每个元素不能相同）
  

• 数值运算：

  V = sum(A)            %列求和
  S = sum(A, 1)     %行求和
  S = sum(sum(A, 1))    %求和
  A = [1:2:11]      %定义矩阵
  B = mean(A)       %均值
  B = max(A)            %极大值
  B = std(A)            %标准方差
  B = corrcoef(A)   %相关系数矩阵
  B = sort(A)       %元素排序

• 符号运算：

  %允许变量不赋值而参与运算；
  f = sym('2*a*x^3')    %字符串
  f = diff(f)           %微积分

• 可视化工具

  1. 具有高层绘图功能——两维、三维绘图
  2. 丰富完备的图像修饰功能
  3. 具有底层绘图功能——句柄绘图
  4. 使用 plot函数 可随时将计算结果可视化

  %示例-三维曲面
  >>D=[0:0.1:5];            %创建向量D
  >>[X,Y]=meshgrid(D);  %创建向量X，Y并赋值为D
  >>Z=4-(X-2).^2-(Y-2).^2;%二元函数
  >>surf(X,Y,Z);            %绘制曲面图
  >>axis off                %关闭坐标轴

• 图形化程序编制功能

  • GUI设计

    %建立一个进度条，监视一个循环语句的进度
    >> h = waitbar(0,'Please wait...');
    steps = 1000;
    for step = 1:steps
    % computations take place here
    waitbar(step / steps)
    end
    close(h)

  • 正弦波发生器

  • van del pol方程（三极管震荡效应）

• 命令窗口

  • help系列（需知道准确的函数名）：
    • help、help + 函数（类）名、helpwin及helpdesk
    • help %显示help 主题一览表
    • help plotxyz %显示有关三维做图指令帮助信息
  • lookfor命令
    • 查找不确切名称函数时，lookfor命令可根据用户提供的关键字，搜索出一组与之相关的命令；
    • lookfor fourier %寻找含有傅立叶变换的相关指令

• 文件格式

  • M文件，以.m为扩展名，所以称为M文件。
    • 由一系列MATLAB语句组成，包括命令文件和函数文件；
    • 命令文件类似于其他高级语言中的主程序或主函数；
    • 函数文件则类似于子程序或被调函数；
    • MATLAB工具箱中的(函数)文件基本上是M函数文件；
    • 可由任一文字处理软件编辑后以文本格式存放。
  • 数据文件，以.mat为扩展名，所以又称MAT文件
    • 数据文件保存了MATLAB工作空间窗口中变量的数据
  • 图形文件，以.fig为扩展名
    • 主要由MATLAB的绘图命令产生，当然也可用File菜单
      中的New命令建立；
  • MEX 文件，以.mex或.dll为扩展名，所以称MEX 文件
    • MEX 实际是由MATLAB Executable缩写而成的，由此可见，MEX文件是MATLAB的可执行文件
  • 模型和仿真文件，模型文件以.mdl为扩展名，仿真文件以.s为扩展名
    • 由Simulink仿真工具箱在建立各种仿真模型时产生。

二、数据类型

1. 特点

• Matlab的基本数据存储类型有十几种，不同专业的工具箱中还有特殊的数据类型，且还支持用户自定义数据类型；
• Matlab数据类型的最大特点是每一种类型都是以数组为基础，把每种类型的数据都作为数组来处理；
• Matlab的默认数据存储类型为双精度浮点类型(double)，可以利用转化函数存储为其它类型；
• 不用事先对变量的类型进行定义或说明，系统会根据变量被赋值的类型自动进行类型识别。

2. 主要数据类型介绍

3. 常量介绍

4. 变量介绍

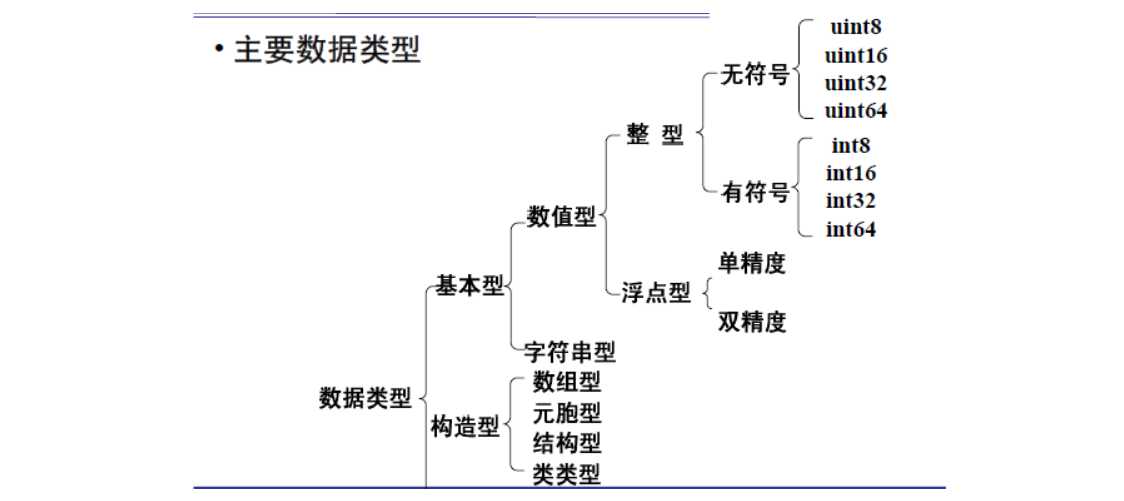
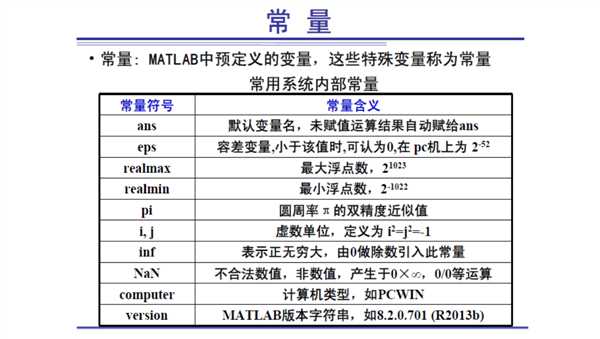
• matlab变量特点

  • 使用前不需要事先声明，也不需要指定变量类型；
  • 所有变量都是以数组或矩阵的形式保存；
  • 赋值过程中，如果变量已经存在，Matlab会用新值代替旧值，并以新的变量类型代替旧的变量类型。

• 变量命名规则

  • 首字母必须为字母

• 变量类型

  • 按生存周期分

    • 局部变量（Local）
    • 全局变量（Global）：全局变量需使用global函数定义，且在任何使用该全局变量的函数中都应加以定义，包括命令窗口
    • 永久变量（Persistent）：类似于static

  • 按数值类型分

    • 数值型变量

      1. 整型变量：

         • 有符号整数（int8, int16, int32, int64）

         • 无符号整数（uint8, uint16, uint32, uint64）

      2. 浮点型变量

         • 单精度（single）：32位（4字节）

         • 双精度（double）：64位（8字节）

         用 intmax(realmax) 和 intmin(realmin) 函数来查询不同整型所能表示的最大整数（浮点数）和最小整数（浮点数）

         浮点数的取整函数

         函数	含义	示例 X = [-1.5, 1.5]
         round(X)	整数部分四舍五入	[-2, 2]
         fix(X)	向0取整	[-1, 1]
         floor(X)	向下取整	[-2, 1]
         ceil(X)	向上取整	[-1, 2]

      3. 复数

         • Matlab表示复数时，可用字母i或j表示虚部(等价)
         • 创建复数可直接输入或利用函数complex(a,b)

    • 逻辑型变量

      • 有两种取值，逻辑真和逻辑假，用“1”和“0”表示

      • 创建逻辑数组
        – 通过输入“true”或“false”直接创建逻辑数组
        – 通过对数组进行逻辑运算创建
        – 通过MATLAB函数产生逻辑数组

      • 

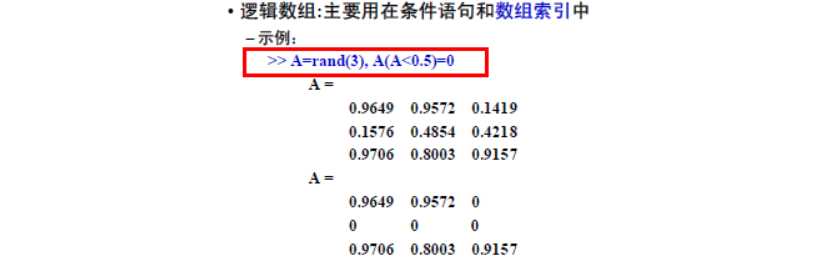
• 变量查询函数

  • who ：列出在matlab工作空间中已经驻留的变量名清单；

  • whos ：whos在给出驻留变量同时，还给出他们的维数及性质

    Name	Size	Bytes	Class	Attributes
    a	1x1	8	double

• 变量删除和内存重组命令

  • clear ：删除所有自定义变量并恢复除eps外所有预定义变量；
  • clear variable1 ：仅删除名为变量variable1的变量；
  • clear variable1 variable2 … ：删除变量variable1 variable2…；
  • clear a* ：删除所有以a开头的变量；
  • pack ：重组和压缩已分配的内存碎块. 当Matlab 的内存满后，可以利用这个命令实现在不清除任何变量的情况下得到更多的空间；
  • pack filename ：用名为filename的文件作为临时文件，重组和
    压缩已分配的内存。

• 数组和矩阵

  • 数组中的元素可以是字符，矩阵中的元素只能是数；

  • 矩阵的乘法、乘方和除法有特殊的数学含义，并不是数组对应元素的运算；

  • 数组或矩阵的创建

    • 直接构造法

    • 增量法

      ? x = i:j %若i<j, 生成以i为初值, j为终值,1为步长的等差数列
      ? x = i:j:k %若i<k, 生成以i为初值, k为终值,j为步长的等差数列
      ? x = i:-j:k %若i>j, 生成以i为初值, k为终值,-j为步长的等差数列
      – 利用linspace(a,b)生成等差向量
      ? x= linspace(2,8) %生成100个数,以2开始,以8结束
      ? y=linspace(2,8,10) %生成10个数,以2开始,以8结束
      – 利用logspace(a,b)生成等比向量
      ? x= logspace(2,8) %生成50个数,以102开始,以108结束
      ? y= logspace(2,8,10)%生成10个数,以102开始,以108结束

  • MATLAB允许对矩阵的单个元素进行赋值和操作，而不影响其他元素的值。如果给出的行下标或列下标大于原来矩阵的行或列，则MATLAB将自动扩展原来的矩阵，并将扩展后未赋值的矩阵元素置为0。

  • 算数运算符

    • 含 . 的是数组操作，是点对点的操作
    • 不含 . 的是矩阵操作，按照矩阵的运算规则

  • 关系运算符

    • 注意：不等于 是 ~=

  • 逻辑运算

    • And、Or、Not、Xor；
    • any(x) ：检测矩阵中是否有非零元素，如果有，则返回1，否则，返回0；
    • all(x) ：检测矩阵中是否全为非零元素，如果是，则返回1，否则，返回0；

  • 优先级

    • 小括号 > 转置、乘方 > 取反 > 乘除 > 冒号 > 关系运算符 > & > |

  • 矩阵的拆分

    • 冒号表达式——A(行号,:) A(:,列号) A(:)

      A(:) 数组A中各列元素首尾相连组成的“一维长列”子数组；
      A(i) "一维长列"子数组中的第i个元素；

    • 利用空矩阵[]。（ X=[]与 clear X 不同：clear是将 X从工作空间中清除，而空矩阵则存在于工作空间，只是维数为 0）

  • 矩阵常见的操作函数

    函数名	含义
    diag	提取对角线元素，或生成对角阵
    flipud	以数组“水平中线”为对称轴，交换上下对称位置上的数组元素
    fliplr	以数组“水平中线”为对称轴，交换上下对称位置上的数组元素
    reshape	在总元素数不变的前提下，改变数组的“行数、列数”
    rot90	矩阵逆时针旋转90度
    det	方阵的行列式
    rank	矩阵的秩

  • 矩阵分解

    • 三角分解（可逆方阵）

      将一个矩阵分解成一个下三角矩阵L和一个上三角矩阵U的乘积，即A=LU，则有[L,U] = lu(A)；

    • 正交分解（满秩方阵）

      将矩阵A分解成一个正交矩阵Q（QQ’=E）与一个上三角矩阵R的乘积A=QR，则有[Q,R,E]=qr(A)；

    • 特征值分解（任意矩阵）

      任意一个n阶方阵X可以分解为XV=VYD，其中D为X的特征值对角阵，V为X的特征向量矩阵，则有 [V,D]=eig(X,Y)

• 字符串（即一维字符数组）

  • 单引号！单引号！单引号！

  • char、num2str、int2str、mat2str 等函数可以将其他的数据类型的变量转化成字符串。

  • isstrprop(‘str’, ‘category’)

    category：alpha-字母，alphanum-字母或数字，cntrl-控制字符串，digit-数字，lower-小写，upper-大写，xdigit-十六进制数

    print，punct

  • 字符串转换函数

    hex2dec hex2num hex2bin num2str int2str stc.

• 函数句柄 ：提供间接调用函数方法的Matlab数据类型

  • 创建：
    • 利用已有函数：fun1=@functionname
    • 提供匿名函数：sqr=@(x)x.^2
  • 调用：与函数一样。

• 元胞数组

  • Matlab所特有的一种数据类型

  • 特点：

    • 组成它的元素是元胞(cell)；
    • 元胞可用来存储不同类型数据的单元；
    • 每个元胞存储一种类型的Matlab数组， 此数组中的数据可以是任何一种Matlab数据类型或用户自定义的类型，其大小也可以是任意的。

  • 创建：

    • 创建元胞数组与创建一般数组基本相同，区别在于一般数组用[]，元胞数组用{}
    • 也可以用 ceil 函数进行构造

  • 使用：

    – 可利用元素地址访问元胞；也可用deal函数查看元胞内容
    >> a={[2 4 7;3 9 6;1 8 5], 'Li Si'; 2+3i,1:2:10}
    >> a{1,2} %查看元胞数组第1行第2列的元胞元素
    ans = Li Si
    >> [a b c d]=deal(a{:}) %用deal函数查看元胞数组内容
    a = 2 4 7
    3 9 6
    1 8 5
    b = 2.0000 + 3.0000i
    c = Li Si
    d = 1 3 5 7 9

  • 转换

    • c = mat2cell(x, m, n)：把矩阵分为子块再转换成元胞数组型。m和n是正整数向量，表示元胞数组行列的大小。m、n中所有元素之和分别是矩阵x的行数和列数；
    • c = mat2cell(x, r)：返回一个列单元数组。正整数向量r各元素之和就是数组x的行数；

  • 显示

    • 直接在命令窗输入单元数组名，可显示单元数组的构成
      单元，显示单元内容可使用celldisp函数；
    • cellplot(A, ‘legend’) ：绘制单元数组结构图。

• 结构数组

  • 类比C语言的结构体，由结构数组变量、域、元素数据三个部分组成。

  • 创建：

    – 利用赋值语句创建结构
    >>student(1).name=‘Zhang San';
    >>student(1).course=[10135 10096];
    >>student(1).score=[87 92]
    – 利用结构函数struct创建结构
    >> student(3) =struct('name','Wang Wu','course',[10568
    10063],'score',[79 86])

  • 添加域：

    - 直接进行赋值
    >>student(1).friend='Tom';
    >>student(2).dad='David';
    - %setfield%

  • 访问：

    – 利用结构数组索引可以对结构数组的字段值或字段元素
    值进行访问或赋值;也可利用getfield函数访问
    >>str1=student(2).name
    str1 = Li Si
    >> getfield(student(2), 'name' )
    ans = Li Si

  • 删除域（注意域名要加单引号）：

    rmfield

三、Matlab程序设计

1. 控制语句

• 顺序结构语句

  • 数据输入
    • 键盘输入：input(‘提示信息‘，‘选项‘)
  • 数据输出
    • disp(输出项)
    • fprintf(‘输出格式‘，输出项)
  • 程序的暂停
    • pause(延迟秒数)
    • pause ：暂停操作，直到用户按任一键后程序继续执行
    • Ctrl+C：强行中止程序

• 循环结构语句

  • for语句

    for 循环变量=表达式1:表达式2:表达式3
    循环体语句
    end
    实例：
    for m=100:999
        m1=fix(m/100);          %求m的百位数字
        m2=rem(fix(m/10),10);   %求m的十位数字
        m3=rem(m,10);           %求m的个位数字
        if m  m1*m1*m1 + m2^3 + power(m3, 3)
            disp(m)
        end
    end

    循环优化

    ? 已知，当n=100时，求y的值。
        y=0; n=100;
        for i=1:n
            y=y+1/(2*i-1);
        end
    ? 在实际MATLAB编程中，采用循环语句会降低其执行速
    度，所以前面的程序通常由下面的程序来代替：
        n=100; i=1:2:2*n-1;
        y=sum(1./i);

  • while语句

    while 表达式
        循环体语句组
    end

  • break和continue

• 条件结构语句

  if 表达式1
    语句组A
  elseif 表达式2
    语句组B
  else 
    语句组C
  end

• 选择结构语句

  switch 表达式
  case 常量表达式1
     语句1
  case 常量表达式2
     语句2
  ...
  otherwise
     语句组n+1
  end
  
  实例：
  price=input('请输入商品价格');
  switch fix(price/100)
    case {0,1} %价格小于200
        rate=0;
    case num2cell(10:24) %价格大于等于1000但小于2500
        rate=8/100;
    otherwise %价格大于等于5000
        rate=14/100;
  end
  price=price*(1-rate) %输出商品实际销售价格

• try-catch语句（lasterr变量）

  – try-catch语句块
  try
    语句组1
  catch
    语句组2
  end
  ? try语句执行语句组1，如执行过程中出现错误，则将错误信息赋给保留的lasterr变量，并转执行语句组2

2. M文件

• 脚本/命令文件（既不接受输入参数也不返回输出参数的M文件称为脚本）

  • 脚本文件中的变量都为全局变量，程序运行后，这些变量保存在Matlab的基本工作空间内，一般采用函数clear清除这些变量；
  • 为了避免因为变量名相同引起冲突，一般在脚本文件的开始，都采用函数clear all，清除所有基本空间中的变量；

• 函数文件（为实现特定功能而定义的供其他程序调用的M文件，有输入输出）

  • 一般以 function 开始；
  • 各种Matlab函数或命令实际上都是函数文件；
  • 函数M文件在执行的过程中，所产生的变量一般都是局部变量，存放在函数自身的函数工作空间中，不会和基本工作空间中的变量产生冲突。

  ? 函数文件组成结构：
    function 返回变量=函数名(输入变量) 
        %帮助文档语句段
  
        %注释说明语句段
        程序语句段
  
  ? 注：
    – 帮助文档语句段就是 `help 函数名` 时对函数的说明内容
    – 具体指：第一个非空行前的所有注释
  ? 输入/输出变量检测命令
    – nargin：在函数体内，用于获取实际输入变量数
    – nargout：在函数体内，用于获取实际输出变量数
    – nargin('fun')：获取'fun'指定函数的标称输入变量数
    – nargout('fun')：获取'fun'指定函数的标称输出变量数
    – inputname(n)：在函数体内使用，给出第n个输入变量数的实际调用变量名

  • “变长度”输入/输出变量

    • Matlab提供了如下两个内置函数
      – varargin：变长度输入变量列表
      – varargout：变长度输出变量列表

3. 程序的调试与优化

• debug指令

  • dbstop in mfile (at lineno)、dbstop if error、dbstop if warning、dbstop if naninf/infnan
  • dbclear（用法与dbstop类似）

  • dbcont、dbstep、dbquit

  • dbstatus

• 耗时分析

  • 相对耗时：profile on profile view profsave profile off
  • 绝对耗时：tic toc

• 程序优化

  

四、Matlab数值运算

1. 数据统计处理

• 求最大与最小元素（max，min）

  >>C = max(X)
  >>[C,I] = max(X) 
  >>C = max(A)
  >>C = max(A,[],dim) %dim=1|2
  >>[C,I] = max(A)
  >>U = max(A,B) 
  >>U = max(A,n)

• 矩阵的平均值与中值（mean，median）

  >>M = mean(X)
  >>M = mean(A)
  >>M = mean(A,dim) %dim=1|2
  %median用法与mean类似

• 矩阵元素求和与求积（sum，prod）

• 矩阵元素的累加和与累乘积（cumsum，cumprod）

  • 注意区分与 sum 和 prod 的关系

• 标准方差（std）

  >>S = std(X)
  >>S = std(A)
  >>S = std(A,flag,dim)

• 相关系数（corrcoef）?

• 元素排序（sort，升序）

2. 复数及其运算

• 创建复数：

  • 直接输入，i或j表示虚部
  • complex(a,b)

• 复数基本运算

  • – 提取实部与虚部可以用函数real、imag
    – 计算模可以用函数abs
    – 计算辐角可以用函数angle
    – 复数的共轭可以用函数conj

• 复数绘图（polar）

  – polar(theta,rho)
  – polar(theta,rho,LineSpec)
  其中，theta为极坐标极角，rho为极坐标矢径，LineSpec为绘制线型

3. 多项式及其运算

• 多项式的创建

  Matlab语言把多项式表达成一个行向量，该向量中的元素是按多项式降幂排列的。

  – 如多项式    f(x)=anxn+an-1xn-1+……+a1x+a0
  – 可用行向量   p=[an an-1 …… a1 a0] 表示

  ? poly函数：产生特征多项式系数向量
    – 调用格式： p=poly(a) %a为多项式的解
    – 特征多项式一定是n+1维的，且第一个元素一定是1
  ? poly2str函数：显示数学多项式的形式
    – 调用格式：p1=poly2str(p, ‘x’) %p为多项式向量，x为变量
  ? 示例:
    >>  a=[1 2 3]; p=poly(a)
    p = 1 -6 11 -6
    >>  p1= poly2str(p, 'x') p2= poly2sym(p, 'x')
    p1 = x^3 - 6 x^2 + 11 x – 6
    P2 = x^3 - 6*x^2 + 11*x - 6

• 多项式的算术运算与求导

  • 乘法：conv(p1, p2) （相当于执行两个数组的卷积）
  • 除法：deconv(p1, p2) （相当于两个数组的解卷）

• 多项式的求值与求根

  • 求根：roots(p) （注意 roots 和 poly 函数可以互换）
  • 求值：
    • ployval(p,x) 对多项式p在x处求值（按数组方式）
    • ployvalm(p,m) 对多项式p在x（方阵）处求值（按矩阵方式）

• 多项式的微积分

  • 微分
    • polyder(p)
    • [p,q] = polyder(a,b)
  • 积分
    • polyint(p,k) ：返回以向量p为系数的多项式的积分，积分的常数项为k（默认为0）

• 多项式部分分式展开

  – [r, p, k] = residue(b, a)：求多项式之比b/a的分式展开，b、a分别为分子和分母多项式系数的行向量，r为留数行向量，p是部分分式的极点，k是常数项
  – 如果多项式a没有重根，展开的形式如下图：
  – 多项式分母有重根时使用resi2命令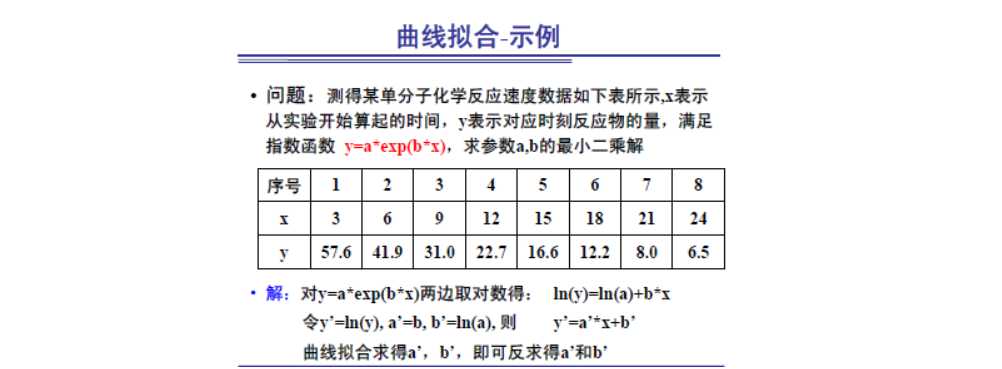

  

4. 曲线拟合与插值

• 曲线拟合 （polyfit）

  – p=polyfit(x, y, n)
  % n表示多项式的最高阶数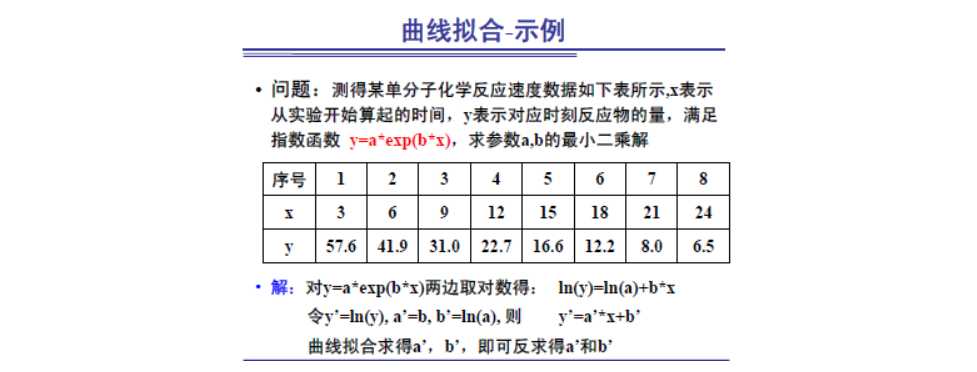

  

  >> x=[3 6 9 12 15 18 21 24];
  >> y=[57.6 41.9 31 22.7 16.6 12.2 8 6.5] ;
  >> yy=log(y); 
  >> p=polyfit(x,yy,1);a=exp(p(2)), b=p(1)
  p = -0.1058 4.3792
  a = 79.7758
  b = -0.1058
  >>xx=3:1:24; plot(x,y,'rd', xx, a*exp(b*xx), 'b-')

• 插值 ？

  是对某些集合给定的数据点之间函数的估值方法，即利用已知点确定未知点。

5. 函数优化

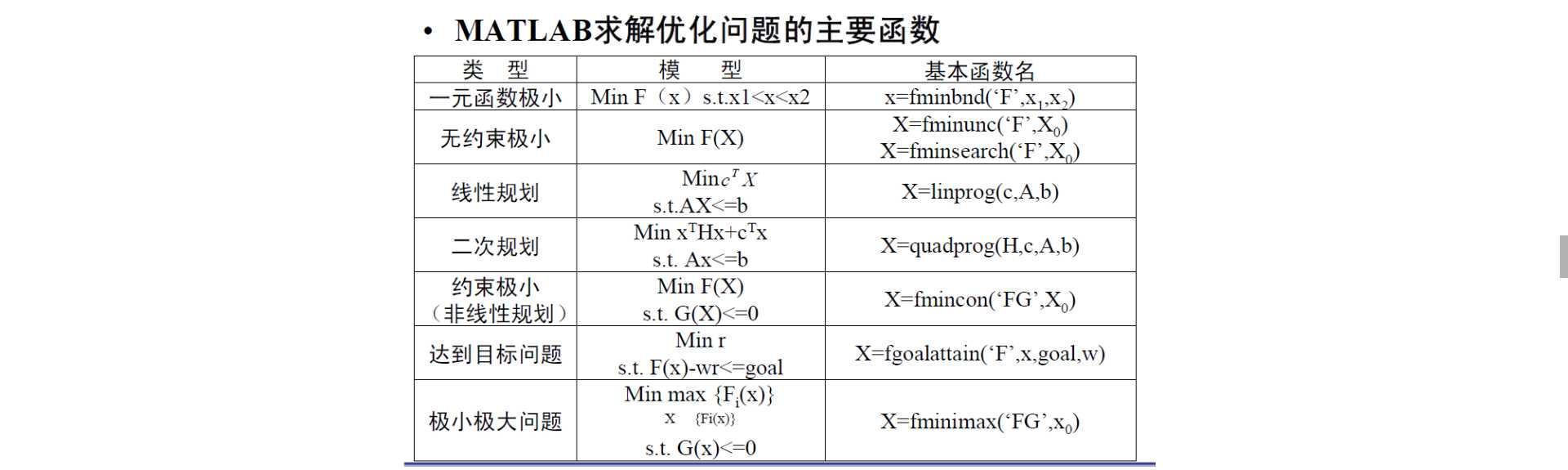
• fminbnd函数：无约束单变量寻优函数；

  ? 调用格式
  – x=fminbnd (fname, x0,x1)：fname 是要求极小值的函数
  名，x0和x1是指定的搜索范围
  

• fminsearch函数：计算多元函数最小值点（在fminsearch中的函数FUN函数的变量为x(1),x(2),...,不能用其它的变量名）

  ? 调用格式
  – [X,FVAL,EXITFLAG,OUTPUT] = fminsearch(FUN,X0)
  – 输入参数：
  ? FUN是函数名,
  ? X0指定初始的搜索位置
  – 输出参数：
  ? X最小值点
  ? FVAL是最小值点处的函数值
  ? EXITFLAG=1表示计算成功
  ? OUTPUT是一个结构数组，记录计算过程的参数
  

6. 代数方程组求解 x=a\b=inv(a)*b

对于代数方程 ax-b=0，其中a 为n×m矩阵
有三种情况：

• 当n=m时，此方程成为“恰定”方程
• 当n>m时，此方程成为“超定”方程
• 当n<m时，此方程成为“欠定”方程

7. 常微分方程求解

• 常微分方程的解析解（dsolve）

  – 函数dsolve用来解符号常微分方程、方程组，如果没有初
  始条件，则求出通解；如果有初始条件，则求出特解
  – r = dsolve('eq1,eq2,...', 'cond1,cond2,...', 'v')
  – ‘eq1,eq2,...’为微分方程或微分方程组
  – ‘cond1,cond2,...’是初始条件或边界条件
  – ‘v’是独立变量，默认的独立变量是't'
  

• 数值解（solver）

  ? 常微分方程的数值解
  – 示例：求解ODE方程y’=-2y+2x2+2x,0 ≤x ≤0.5, y(0)=1 的
  解
  – y=dsolve(‘Dy=-2*y+2*x^2+2*x’,‘y(0)=1’,‘x’);%解析解
  – x=0:0.01:0.5; yy=subs(y,x);
  – fun=inline('-2*y+2*x*x+2*x');
  – [x,y]=ode15s(fun,[0:0.01:0.5],1); %数值解
  – plot(x,yy,‘r’,x,y,‘b’)
  

五、Matlab符号运算（Maple）

1. 定义 符号对象

• sym函数：用于创建单个符号对象

  – S=sym(A , flag)：定义符号对象S
  – A可以是常量、变量、函数或表达式
  – flag可选择d、f、e或r，缺省/默认为r
  ? d表示返回最接近的十进制数值（默认为32位）
  ? f表示返回最接近的浮点值(N*2^e形式，N和e都为整数)
  ? e表示返回最接近的带有机器浮点误差的有理值
  ? r表示返回最接近的有理表示（两个整数p和q构成的p/q、p*q 、10^q 、pi/q 、2^q 、sqrt(p) 等形式）
  

• syms 函数：一次创建多个符号对象

  – syms ('符号变量名1','符号变量名2',...,'符号变量名n')
  – syms ‘符号变量名1’ ‘符号变量名2’…‘符号变量名n’
  – syms 符号变量名1 符号变量名2 ... 符号变量名n clear %只能用空格隔开
  

2. 创建 符号表达式

• 用字符串
• 用sym函数
• 用符号对象

3. 创建 符号矩阵

• 使用sym 函数直接生成

  A=sym('[1+x, sin(x); 5, exp(x)]')
  

• 将数值矩阵转化成符号矩阵

  B=[2/3, sqrt(2); 5.2, log(3)];
  C=sym(B)
  

• 引用

4. 符号运算

• numden(s) 函数（通分）

  ? [N,D]=numden(f): N 为通分后的分子，D 为通分后的分母
  

• factor(s) 函数（因式分解）

  >> syms x; f=x^6+1, factor(f)
  f = x^6 + 1
  ans = (x^2 + 1)*(x^4 - x^2 + 1)
  – 也可用于正整数的分解，大整数分解要转化成符号常量
  >> factor(100)
  >> factor(sym('12345678901234567890'))
  

• expand(s) 函数（表达式展开）

• collect 函数（合并同类项）

  – collect(s)： 对符号表达式s合并同类项
  – collect(s, v) ：对符号表达式s按变量v合并同类项
  

• 

• sym2poly, poly2sym（与多项式的转换）

5. 符号数值精度控制

• 数值型： MATLAB的浮点运算，运算速度最快；

• 有理数型： Maple的精确符号运算，运算结果准确，计算时间、占用内存最大；

• VPA型： Maple的任意精度运算。

• 精度控制函数

  – digits： 用来显示当前计算精度位数，默认为32位
  – digits(n)： 设置计算数值型结果时以n位相对精度进行
  – xr=vpa(x): 给出x在digits指定精度下的数值型结果xr
  – xr=vpa(x,n): 给出x在n位相对精度下的数值型结果xr

6. 符号变量的查找：findsym 函数

findsym(s, n)：函数返回符号表达式s中的n个符号变量，若没有指定n，则返回s中的全部符号变量(不按顺序)

符号表达式中如果有多个字符变量，则按照以下顺序选择自由变量：

1. 首先选择x作为自由变量；
2. 如果没有x，则选择在字母顺序中最接近x的字符变量；
3. 如果与x相同距离，则在x后面的优先；
4. 大写字母比所有的小写字母都靠后。

7. 符号变量的替换：subs 函数

– subs(f,a)：用a替换符号表达式f 中的(第一)自由变量
– subs(f,x,a) ：用a 替换符号表达式f 中指定的符号变量x
– a可以是数/数值变量/表达式或字符变量/表达式

8.符号极限函数： limit函数

9. 符号导数函数：diff 函数

– g=diff(f)： 求符号表达式f 关于默认变量的导数
– g=diff(f,v)： 求符号表达式f 关于变量v 的导数
– g=diff(f, n)：求f 关于默认变量的n 阶导数
– g=diff(f,v,n)：求f 关于变量v 的n 阶导数

10. 符号积分函数 int函数

11. 符号代数方程的求解 solve函数

12. 符号函数的可视化 在对应的数值函数名加前缀 ez

• 曲线：ezplot, explot3
• 等高线：ezcontour(f)
• 三维网格图：ezmesh(f)
• 三维曲面图：ezsurf(f)
• 极坐标曲线：ezpolar(f)

六、Matlab图形绘制

1. plot函数

– plot(Y)：如果Y为实向量，则以Y的索引坐标作为横坐标，
以Y本身的元素作为纵坐标；如果Y为复数向量，则以该向
量实部为横坐标，虚部为纵坐标
– plot(X,Y)：以X、Y为横、纵坐标；X和Y维数必须相同；
当X和Y是同阶矩阵时，将按照矩阵的行或列进行操作
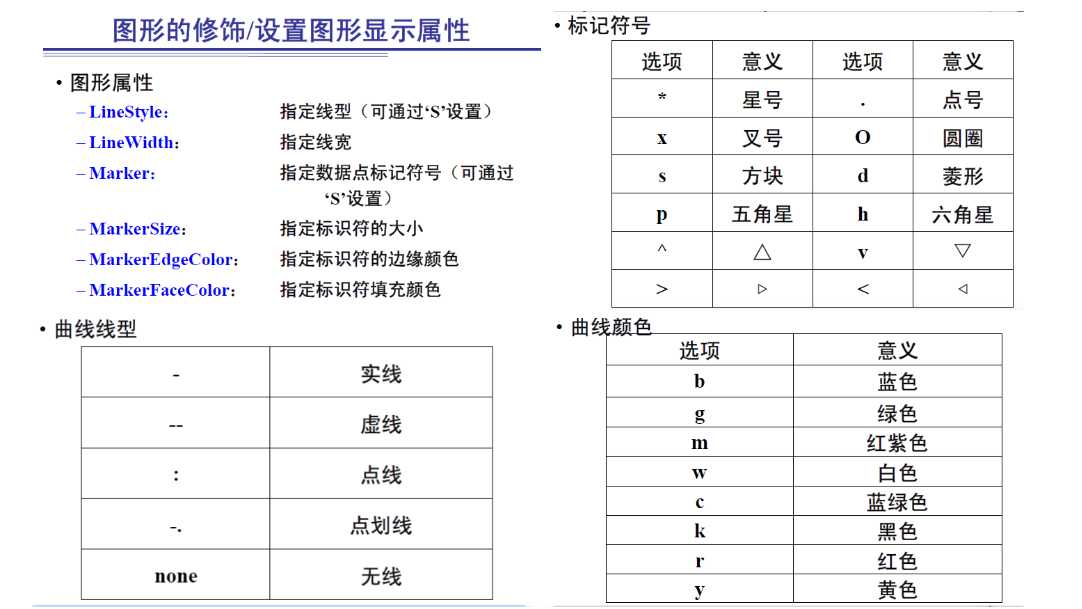
– plot(X,Y,s)：第三个变量用于设置图形显示属性。设置图
形的线型、颜色、标记等
– plot(X,Y,’PropName’, PropVal)：设置图形属性
– plot(X1,Y1,s1,X2,Y2,s2,…..) ：每三项为一组绘制多条曲线

2. polar函数：用于绘制极坐标图

– polar(theta, rho)：用极角theta和极径rho绘制极坐标图
– polar(theta, rho, s)：使用s指定极坐标图中线条的颜色
、类型与记号类型等

3. 图形的文字标注：在图形中添加标识性的注释

• title(s)：添加图名；其中s代表图名，为字符串
• xlabel(s)：添加横坐标轴名
• ylabel(s)：添加纵坐标轴名
• legend(s, position)：在指定位置建立图例
  • 参数s是图例中的文字注释，可用‘s1’, ‘s2’, … 的方式
  • 参数position指定图例在图上位置，可取值0(自动最佳位置)、1(默认，右上角)、2(左上角)、3(左下角)、4(右下角)、-1(图右侧)
• text(x, y, s)：在图形中的点(x, y)处添加文字注释

4. 多重叠绘制图形 hold函数

• hold：双向切换
• hold on / off

5. 多子图 subplot函数

– subplot(m, n, k)：将同一个图形窗口分割为m行n列个子
窗口（或称子图），k是子图的编号，编号顺序是自左向
右，再自上而下，所产生的子图分割按照此编号顺序（
为默认值）自动进行；
– subplot(‘position’, [left bottom width height])：在指定位置上分割子图，并成为当前图；以左下角为原点，位置
取值[0, 1]；
– 所有子图彼此独立，所有的绘图命令可以在子图中使用。

6. 多窗口绘图 figure(n)

创建绘图窗口函数，n为窗口顺序号。

7. 坐标轴控制 axis函数

? axis函数：控制坐标轴的可视、取向、高宽比等
– axis auto：使用默认设置
– axis equal：纵、横坐标采用等长刻度
– axis manual：使当前坐标范围不变
– axis fill：manual方式下起作用，使坐标充满整个绘图区
– axis on：使用轴背景
– axis off：取消轴背景
– axis image：纵横坐标采用等长刻度且坐标框紧贴数据范围
– axis xy：普通直角坐标系，原点在左下方
– axis ij：矩阵式坐标，原点在左上方
– axis square：产生正方形坐标系
– axis normal：默认矩形坐标系
– axis tight：把数据范围直接设为坐标范围
– axis([xmin, xmax, ymin, ymax])：设定坐标范围

8. 网格线开关-grid函数 坐标框开关-box函数

9. 三维曲线图 plot3 函数

10. 三维网格图 mesh函数

（与之相对应的绘制符号函数三维效果的分别为 ezplot3 和 ezmesh）

11. 三维曲面图 surf 和 meshgrid 函数

• surf：曲面图是网格图的涂色版本；
• meshgrid(x,y)：用来生成二元函数z=f(x,y)中X-Y平面上
  的矩形定义域中数据点矩阵X与Y

>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);
Z = X .* exp(-X.^2 - Y.^2);
surf(X,Y,Z)

12. 三维图形修饰处理

• view函数 ：控制三维图形的观察点和视角；
• viewmtx ：用来计算一个4×4阶的正交或透视的转换
  矩阵，该矩阵将一个四维向量转换到一个二维的视平面
  上（如计算机平面）上；
• colormap函数：图形颜色的修饰
• alpha函数：设定曲面对象的透明度；还可以设置
  当前坐标轴内绘图对象的透明程度

七、Simulink

1. 流程

1. 创建空白模型
2. 添加模块
3. 添加连接
4. 仿真配置
5. 运行仿真
6. 保存模型

八、图像处理

1. 数像生成过程

• 采样（空间离散）：二值、灰度、彩色、立体、三维……
• 量化（灰度离散）
• 编码（实现图像传输与存储的关键）

2. 图像存储

• 矢量图：计算机指令，点线面，不易失真；
• 点阵图（位图）：像素点，易失真。

3. 图像处理

• imread(filename, fmt)
• imwrite(A, filename, fmt)
• imfinfo(filename)
• load/save *.mat 装载和存储数据，数据格式为MAT文件
• imshow：显示
• truesize(FIG, [R,C])：调整图像大小
• 图像运算
  • imadd(I, J)
  • imsub(I, J)
  • immultiply(I, n)：亮度缩放
  • immultiply(I, mask)：掩模运算
  • imdivide(I,n)：亮度缩放
  • imdivide(I,J) ：除掉北京

课后习题

重要函数

BUAA_2019_MATLAB基础与应用_期末复习纲要

标签：域名   文件   eal   actor   开关   语句   printf   while语句   离散   

原文地址：https://www.cnblogs.com/FUJI-Mount/p/12134155.html