标签:cst n+1 eve || init png printf 元素 src
先说句新年好哈哈哈
今年又是颓废的一年呢。。。
(开始就满满负能量真好)

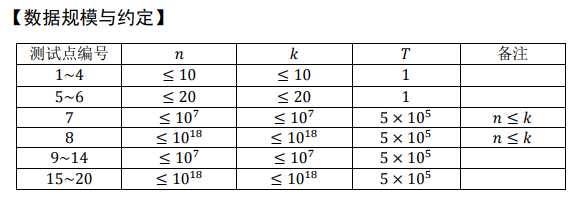
分析:
真是有趣的数学递推找规律问题呢。。。
考场上没想出来,然后n2^n的状压也想不到
索性20*20直接打表2333。。。
对于排列S(n,m)如果m>=2*n-1那么怎么放都不会影响,于是就是全排列前缀和了。。
然后怎么求
然后我们灵(da)光(biao)一(kan)闪(kan)惊奇的发现N大于MOD的阶乘就不用算了,模下来一定是0
到现在你已经有了40分的高分(大雾
接下来进入正解:
对于S(n,m),如果m<=n不用算了,无解
于是考虑n<m<2*n-1的情况
首先对于前m-n个元素,随便放都不会影响结果
然后第m-n+1号元素,也可以随意放,有m-n+1种选择
但这样对于第n号元素,就只有m-n种选择了
此时对于m-n+2号元素,刚好还有m-n+1种选择
但这样对于n-1号元素,只有m-n种选择
以此类推。。。我们得出了递推式:
S(n,m) = (m-n) ! * (m-n+1) ^ ((i-k)/2上取整) * (m-n) ^ ((i-k)/2下取整)
然后大力推S(i,i+k),本质就是等比数列求和

#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define maxn 21 #define MOD 20000023 using namespace std; inline long long getint() { long long num=0,flag=1;char c; while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1; while(c>=‘0‘&&c<=‘9‘)num=num*10+c-48,c=getchar(); return num*flag; } int fac[MOD],sum[MOD]; long long n,K; inline void init() { fac[1]=1; for(int i=2;i<MOD;i++)fac[i]=1ll*fac[i-1]*i%MOD; for(int i=1;i<MOD;i++)sum[i]=(sum[i-1]+fac[i])%MOD; } inline long long ksm(long long num,long long k) { long long ret=1; for(;k;k>>=1,num=num*num%MOD)if(k&1)ret=ret*num%MOD; return ret; } int main() { int T=getint(); init(); while(T--) { n=getint(),K=getint(); if(n<=K+1)printf("%d\n",sum[min(n,1ll*(MOD-1))]); else if(K+1>=MOD)printf("%d\n",sum[MOD-1]); else { int k=n-K,ans=sum[K-1]; int A=1ll*K*(K+1)%MOD; int inv=ksm(A-1,MOD-2); ans=(ans+1ll*fac[K]*(ksm(A,k/2+1)-1)%MOD*inv%MOD)%MOD; ans=(ans+1ll*fac[K]*(ksm(A,(k-1)/2+1)-1)%MOD*(K+1)%MOD*inv%MOD)%MOD; printf("%d\n",ans); } } }

标签:cst n+1 eve || init png printf 元素 src
原文地址:https://www.cnblogs.com/Darknesses/p/12142147.html