PLSA

标签：之间   存在   抽取   http   计算   let   info   知识   估计   

首先，回顾一元模型，然后引出贝叶斯学派的一元模型；

如图示：

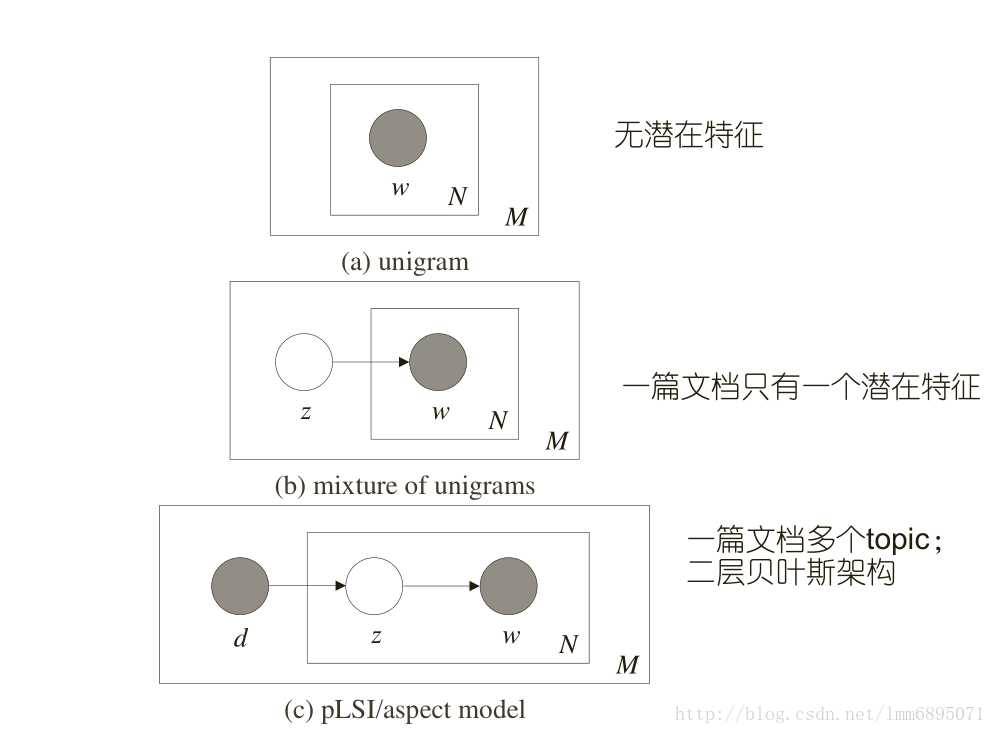
一元模型中，不存在潜在主题，我们产生word的过程，相当于投骰子（V面）；那么整个文档集的分布是：(文档直接独立，word之间独立)
p(W)=∏dD∏iNp(wi)=∏dD∏vVp(wv)cv
p(W)=∏dD∏iNp(wi)=∏dD∏vVp(wv)cv

然后通过最大似然方法获得参数，p(wi)^=ciCp(wi)^=ciC,CC是总的頻数；
混合一元模型：
这里，我们假定，一篇文档有一个主题z，因此，
p(W,z|d)=p(z|d)∏iNp(wi|z)p(W|d)=∑zp(z|d)∏iNp(wi|z)
p(W,z|d)=p(z|d)∏iNp(wi|z)p(W|d)=∑zp(z|d)∏iNp(wi|z)
以上频率学派思想，现在，利用贝叶斯学派思想，重新思考模型：
现在有一个坛子，里面有无穷多个骰子（V面）;现在，我们首先得抽取一个骰子，然后才能进行计算；我们假定选取过程是服从Dirichlet分布的（先验)，因为我们知道，投骰子时，获得word的頻数是服从多项式分布的；这样后验概率也是Dirichlet分布；
这里先验参数是θθ,那么
p(W,θ)=p(θ)p(W|θ)p(W)=∫p(θ)p(W|θ)dθ=∫p(θ)∏p(wi|θ)dθ
p(W,θ)=p(θ)p(W|θ)p(W)=∫p(θ)p(W|θ)dθ=∫p(θ)∏p(wi|θ)dθ
我们回顾了基础知识；现在我们来分析一下PLSA模型，概率图模型如图C所示；可以看到，每一篇文档含有多个主题；；
现在，我们生成文档的过程是：我们投骰子（K面，代表文档-主题概率）获得主题z，然后寻找到主题为z的那个主题-word骰子，然后投骰子获得word;
即：
p(wi|dm)=∑zp(wi|z)p(z|dm)p(W|dm)=∏iN∑zp(wi|z)p(z|dm)=∏iN∑zθwi,z?dm
p(wi|dm)=∑zp(wi|z)p(z|dm)p(W|dm)=∏iN∑zp(wi|z)p(z|dm)=∏iN∑zθwi,z?dm
这里可以使用EM算法，最大似然方法进行模型估计；

PLSA

标签：之间   存在   抽取   http   计算   let   info   知识   估计   

原文地址：https://www.cnblogs.com/lxt-/p/12150089.html