CTR预估---传统模型

时间：2020-01-06 17:43:21 阅读：815 评论：0 收藏：0 [点我收藏+]

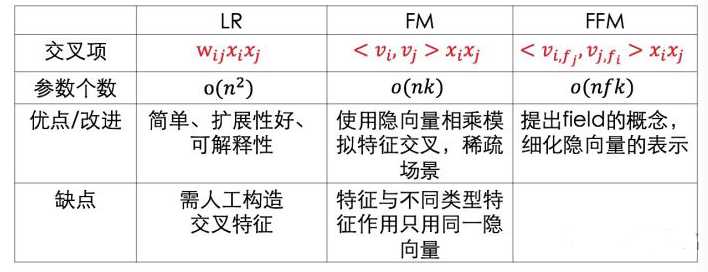
传统CTR预估模型包括：LR、FM、GBDT等，其优点是：可解释性强、训练和部署方便、便于在线学习。

技术图片

（一）CTR预估

1.在cost-per-click：CPC广告中广告主按点击付费。为了最大化平台收入和用户体验，广告平台必须预测广告的CTR，称作predict CTR：pCTR。对每个用户的每次搜索query，有多个满足条件的广告同时参与竞争。只有pCTR x bid price最大的广告才能竞争获胜，从而最大化eCPM：eCPM=pCTR x bid

　　基于最大似然准则可以通过广告的历史表现得统计来计算 pCTR 。假设广告曝光了 100次，其中发生点击 5 次，则 pCTR = 5%。其背后的假设是：忽略表现出周期性行为或者不一致行为的广告，随着广告的不断曝光每个广告都会收敛到一个潜在的真实点击率 CTR_true 。

　　这种计算 pCTR 的方式对于新广告或者刚刚投放的广告问题较大：

新广告没有历史投放信息，其曝光和点击的次数均为 0 。
刚刚投放的广告，曝光次数和点击次数都很低，因此这种方式计算的 pCTR 波动非常大。

　　如：一个真实 CTR 为 5% 的广告必须曝光 1000次才有 85% 的信心认为 pCTR 与真实 CTR 的绝对误差在1% 以内。真实点击率越低，则要求的曝光次数越多。为解决这个问题，论文 《Predicting Clicks: Estimating the Click-Through Rate for New Ads》 提出利用 LR 模型来预测新广告的CTR。

2.从经验上来看：广告在页面上的位置越靠后，用户浏览它的概率越低。因此广告被点击的概率取决于两个因素：广告被浏览的概率、广告浏览后被点击的概率。因此有：

$p(click|ad,pos)=p(click|ad,pos,seen) \times p(seen|ad,pos)$

假设：

　　在广告被浏览（即：曝光）到的情况下，广告被点击的概率与其位置无关，仅与广告内容有关。

　　广告被浏览的概率与广告内容无关，仅与广告位置有关。

则有：

p(click|ad,pos)=p(click|ad,seen)xp(seen|pos)

第一项p(click|ad,seen)就是我们关注和预测的CTR。

第二项与广告无关，是广告位置（即：广告位）的固有属性。

可以通过经验来估计：统计该广告位的总拉取次数impress（pos），以及总曝光次数see（pos），则：

$p(seen|pos)=\frac{seen(pos)}{impress(pos)}$，这也被称为广告位的曝光拉取比。

（二）算法

一、LR模型　

1.论文将CTR预估问题视作一个回归问题，采用逻辑回归LR模型来建模，因为LR模型的输出在【0,1】之间。$pCTR=\frac{1}{1=exp(-\sum_i w_i f_i)}$

其中$f_i$表示从广告中抽取的第$i$个特征（如广告标题的单词数量），$w_i$为该特征对应的权重。采用符号的原因是使得权重、特征和pCTR正相关：权重越大则pCTR越大。

2.评价标准

模型通过L-BFGS算法来训练；

损失函数：交叉熵 L=-[pCTR]xlog(CTR)+(1-pCTR)xlog(1-CTR)]

权重通过均值为0、方差为$\sigma$的高斯分布来随机初始化。其中$\sigma$为超参数，其取值集合为[0.01,0.03,0.1,0.3,1,3,10,30,100]，并通过验证集来选取最佳的值。

评估指标：测试集上每个广告的pCTR和真实点击率的平均KL散度。KL散度衡量了pCTR和真实点击率之间的偏离程度。一个理想的模型，其KL散度为0，表示预估点击率和真实点击率完全匹配。$\overline{\mathbb{D}}_{K L}=\frac{1}{T} \sum_{i=1}^{T}\left(\operatorname{pCTR}\left(\operatorname{ad}_{i}\right) \times \log \frac{\operatorname{pCTR}\left(\operatorname{ad}_{i}\right)}{\operatorname{CTR}\left(\operatorname{ad}_{i}\right)}+\left(1-\operatorname{pCTR}\left(\operatorname{ad}_{i}\right)\right) \times \log \frac{1-\operatorname{pCTR}\left(\operatorname{ad}_{i}\right)}{1-\overline{\operatorname{CTR}}\left(\operatorname{ad}_{i}\right)}\right)$

3.模型不仅可以用于预测新广告的pCTR，还可以为客户提供优化广告的建议。可以根据模型特征及其重要性来给广告主提供创建广告的建议，如：广告标题太短建议增加长度。

二、Degree-2 Polynomial Margin (Poly2)

1.LR模型只考虑特征之间的线性关系，而POLY2 模型考虑了特征之间的非线性关系。

　　捕获非线性特征的一个常用方法是采用核技巧，如高斯核RBF，将原始特征映射到一个更高维空间。在这个高维空间模型是线性可分的，即：只需要考虑新特征之间的线性关系。但是核技巧存在计算量大、内存需求大的问题。

　　论文 Training and Testing Low-degree Polynomial Data Mappings via Linear SVM 提出多项式映射 polynomially mapping 数据的方式来提供非线性特征，在达到接近核技巧效果的情况下大幅度降低内存和计算量。

2.设低维样本空间为n维度，低维样本$x={x_1,...,x_n}^T$。

多项式核定义为：$K(x_i,x_j)=(\gamma x_i*x_j+r)^d$，其中$\gamma,r$为超参数，$d$为多项式的度degree。

根据定义，多项式核等于样本在高维空间向量的内积$K\left(\overrightarrow{\mathbf{x}}_{i},\overrightarrow{\mathbf{x}}_{j}\right)=\phi\left(\overrightarrow{\mathbf{x}}_{i}\right) \cdot\phi\left(\overrightarrow{\mathbf{x}}_{j}\right)$，其中，$\phi$为映射函数。

当$d=2$时，有$\phi(\overrightarrow{\mathbf{x}})=\left[1, \sqrt{2 \gamma} x_{1}, \cdots, \sqrt{2 \gamma} x_{n}, \gamma x_{1}^{2}, \cdots, \gamma x_{n}^{2}, \sqrt{2} \gamma x_{1} x_{2}, \cdots, \sqrt{2} \gamma x_{n-1}x_{n}\right]^{T}$，使用$\sqrt{2}$是为了$\phi(x_i)\phi(x_j)$的表达更简洁。

3.如果不用核技巧，仅仅考虑使用一个多项式映射，则我们得到：$\phi(\overrightarrow{\mathbf{x}})=\left[1, x_{1}, \cdots, x_{n}, x_{1}^{2}, \cdots, x_{n}^{2}, x_{1} x_{2}, \cdots, x_{n-1} x_{n}\right]^{T}$

结合LR模型，则得到POLY2模型：

$z(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{n} w_{i} \times x_{i}+\sum_{i=1}^{n} \sum_{j=i}^{n} w_{i, j} \times x_{i} \times x_{j}$，
$y(\overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (-z(\overrightarrow{\mathbf{x}}))}$

新增的组合特征一共有$\frac{n(n-1)}{2}$个。

4.POLY2模型的优缺点：

（1）优点：除了线性特征之外，还能够通过特征组合自动捕获二阶特征交叉产生的非线性特征。

（2）缺点：

　　参数空间大幅增加，由线性增加至平方级（如计算广告场景中，原始样本特征可能达到上万甚至百万级别，则特征的交叉组合达到上亿甚至上万亿。）

　　数据稀疏导致二次项参数训练困难，非常容易过拟合。

三、FM（Factorization Machine）

1.推荐系统中的评分预测用户，给定用户集合$U=\{u_1,u_2,...,u_M\}$、物品集合$I=\{i_1,i_2,...,i_N\}$，模型是一个评分函数$f$，$y=f(u,i)$表示用户$u$对物品$i$的评分。目标是求解剩余用户在剩余物品上的评分。

通常评分问题是一个回归问题，模型预测结果是评分的大小，此时损失函数采用MAE/MSE等。
也可以将其作为一个分类问题，模型预测结果是各评级的概率，此时损失函数为交叉熵。
当评分只有0和1时，这表示用户对商品"喜欢/不喜欢"，或者"点击/不点击"，这就是典型的点击率预估问题。

2.事实上除了已知部分用户在部分物品上的评分之外，通常还能够知道一些有助于影响评分的额外信息。如：用户画像、用户行为序列等等。这些信息称作上下文 context。

对每一种上下文，我们用变量$c$来表示，$C$为该上下文的取值集合。假设所有的上下文为$C_3,...,C_K$，则模型为$f: \mathbb{U} \times \mathbb{I} \times \mathbb{C}_{3} \times \cdots \times \mathbb{C}_{K} \rightarrow \mathbb{R}$，上下文的下标为3开始，因为可用认为用户$u$和商品$i$也是上下文的一种。

如下图所示为评分矩阵，其中

$\mathbb{U}=\{\mathrm{A}, \mathrm{B}, \mathrm{C}\}, \quad \mathbb{I}=\{\mathrm{TI}, \mathrm{NH}, \mathrm{SW}, \mathrm{ST}\}$，$\mathbb{C}_{3}=\{\mathrm{S}, \mathrm{N}, \mathrm{H}\}, \quad \mathbb{C}_{4}=\{\mathrm{A}, \mathrm{B}, \mathrm{C}\}$ $y \in\{1,2,3,4,5\}$

所有离散特征都经过特征转换。

技术图片

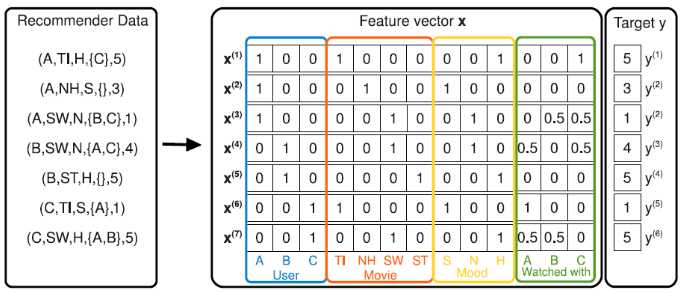
3.上下文特征context类似属性property特征，它和属性特征的区别在于：

属性特征是作用到整个用户（用户属性）或者整个物品（物品属性），其粒度是用户级别或者物品级别。如：无论用户 “张三” 在在评分矩阵中出现多少次，其性别属性不会发生改变。
上下文特征是作用到用户的单个评分事件上，粒度是事件级别，包含的评分信息更充足。如：用户 ”张三“ 在评价某个电影之前已经看过的电影，该属性会动态改变。

事实上属性特征也称作静态画像，上下文特征也称作动态画像。业界主流的做法是：融合静态画像和动态画像。另外，业界的经验表明：动态画像对于效果的提升远远超出静态画像。

4.FM模型

来自论文：《Fast Context-aware Recommendations with Factorization Machines》

和 POLY2 相同FM 也是对二路特征交叉进行建模，但是FM 的参数要比 POLY2 少得多。

将原本重写为：$\overrightarrow{\mathbf{x}}=\left(x_{1}, x_{2}, x_{3}, \cdots, x_{K}\right)^{T}=\left(u, i, c_{3}, \cdots, c_{K}\right)^{T}$

则FM模型为：$\hat{y}(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\sum_{i=1}^{K} \sum_{j=i+1}^{K} \hat{w}_{i, j} \times x_{i} \times x_{j}$

其中，$\hat{w}_{i, j}$是交叉特征的参数，它有一组参数定义：$\hat{w}_{i, j}=<\overrightarrow{\mathbf{v}}_{i}, \overrightarrow{\mathbf{v}}_{j}>=\sum_{l=1}^{d} v_{i, l} \times v_{j, l}$

即：$\hat{\mathbf{W}}=\left[\begin{array}{cccc}{\hat{w}_{1,1}} & {\hat{w}_{1,2}} & {\cdots} & {\hat{w}_{1, K}} \\ {\hat{w}_{2,1}} & {\hat{w}_{2,2}} & {\cdots} & {\hat{w}_{2, K}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\hat{w}_{K, 1}} & {\hat{w}_{K, 2}} & {\cdots} & {\hat{w}_{K, K}}\end{array}\right]=\mathbf{V}^{T} \mathbf{V}=\left[\begin{array}{c}{\overrightarrow{\mathbf{v}}_{1}^{T}} \\ {\overrightarrow{\mathbf{v}}_{2}^{T}} \\ {\vdots} \\ {\overrightarrow{\mathbf{v}}_{K}^{T}}\end{array}\right]\left[\begin{array}{cccc}{\overrightarrow{\mathbf{v}}_{1}} & {\overrightarrow{\mathbf{v}}_{2}} & {\cdots} & {\overrightarrow{\mathbf{v}}_{K}}\end{array}\right]$

模型待求解的参数为：

$w_{0} \in \mathbb{R}, \overrightarrow{\mathbf{w}} \in \mathbb{R}^{n}$
$\mathbf{V}=\left(\overrightarrow{\mathbf{v}}_{1}, \cdots, \overrightarrow{\mathbf{v}}_{K}\right) \in \mathbb{R}^{d \times K}$

其中：

$w_0$表示全局偏差；
$w_i$用于捕获第$i$个特征和目标之间的关系
$\hat{w}_{i,j}$用于捕获$(i,j)$二路交叉特征和目标之间的关系。
$\overrightarrow{\mathbf{v}}_{1}$，它是$\mathbf{V}$的第$i$列。

5.FM模型的计算复杂度为$O(K \times K \times d)=O\left(K^{2} d\right)$，但是经过数学转换之后其计算复杂度可以降低到$O(Kd)$:

$\sum_{i=1}^{K} \sum_{j=i+1}^{K} \hat{w}_{i, j} \times x_{i} \times x_{j}=\sum_{i=1}^{K} \sum_{j=i+1}^{K} \sum_{l=1}^{d} v_{i, l} \times v_{j, l} \times x_{i} \times x_{j}$
$=\sum_{l=1}^{d}\left(\sum_{i=1}^{K} \sum_{j=i+1}^{K}\left(v_{i, l} \times x_{i}\right) \times\left(v_{j, l} \times x_{j}\right)\right)$
$=\sum_{l=1}^{d} \frac{1}{2}\left(\left(\sum_{i=1}^{K} v_{i, l} \times x_{i}\right)^{2}-\sum_{i=1}^{K} v_{i, l}^{2} \times x_{i}^{2}\right)$

因此有：

$\hat{y}(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\frac{1}{2} \sum_{l=1}^{d}\left(\left(\sum_{i=1}^{K} v_{i, l} \times x_{i}\right)^{2}-\sum_{i=1}^{K} v_{i, l}^{2} \times x_{i}^{2}\right)$

其计算复杂度为$O(Kd)$

6.FM模型可以用于求解分类问题（预测各评级的概率），也可以用于求解回归问题（预测各评分大小）。

对于回归问题，其损失函数为MSE：$\mathcal{L}=\sum_{(\overrightarrow{\mathbf{x}}, y) \in \mathbb{S}}(\hat{y}(\overrightarrow{\mathbf{x}})-y)^{2}+\sum_{\theta \in \Theta} \lambda_{\theta} \times \theta^{2}$

对于二分类问题，其损失函数为交叉熵：

$\phi(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\frac{1}{2} \sum_{l=1}^{d}\left(\left(\sum_{i=1}^{K} v_{i, l} \times x_{i}\right)^{2}-\sum_{i=1}^{K} v_{i, l}^{2} \times x_{i}^{2}\right)$
$p(\hat{y}=y | \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (-y \phi(\vec{x}))}$
$\mathcal{L}=\left(-\sum_{(\vec{x}, y) \in \mathbb{S}} \log p(\hat{y}=y | \vec{x})\right)+\sum_{\theta \in \Theta} \lambda_{\theta} \times \theta^{2}$

其中：评级集合为$y \in\{-1,1\}$一共两个等级

$p(\hat{y}=y | \overrightarrow{\mathbf{x}})$为样本$\overrightarrow{x}$预测为评级$y$的概率，满足：

$p(\hat{y}=1 | \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (-\phi(\overrightarrow{\mathbf{x}}))}$
$p(\hat{y}=-1 | \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (\phi(\overrightarrow{\mathbf{x}}))}$

损失函数最后一项是正则化项，为了防止过拟合，$\Theta=\left\{w_{0}, \overrightarrow{\mathbf{w}}, \mathbf{V}\right\}$。其中$\lambda_{\theta}$为参数$\theta$的正则化参数，它是模型的超参数。

可以针对每个参数配置一共正则化系数，但是选择合适的值需要进行大量的超参数选择。论文推荐进行统一配置：

对于$w_0$，正则化系数为$\lambda_{w_0}=0$，这表示不需要对全局偏差进行正则化。
对于$w_i$，统一配置正则化系数为$\lambda_w$
对于$v_{i,l}$，统一配置正则化系数为$\lambda_v$

7.FM可以处理不同类型的特征：

离散型特征 categorical：FM 对离散型特征执行 one-hot 编码。如，性别特征：“男” 编码为 (0,1)，“女” 编码为 (1,0) 。
离散集合特征 categorical set：FM 对离散集合特征执行类似 one-hot 的形式，但是执行样本级别的归一化。如，看过的历史电影。假设电影集合为：“速度激情9，战狼，泰囧，流浪地球”。如果一个人看过 “战狼，泰囧，流浪地球”，则编码为(0,0.33333,0.33333,0.33333) 。
数值型特征 real valued：FM直接使用数值型特征，不做任何编码转换。

8.FM的优势：

给定特征 representation 向量的维度时，预测期间计算复杂度是线性的。
在交叉特征高度稀疏的情况下，参数仍然能够估计。 因为交叉特征的参数不仅仅依赖于这个交叉特征，还依赖于所有相关的交叉特征。这相当于增强了有效的学习数据。
能够泛化到未被观察到的交叉特征。 设交叉特征 “看过电影 A 且年龄等于20” 从未在训练集中出现，但出现了 “看过电影 A”相关的交叉特征、以及 “年龄等于20”相关的交叉特征。于是可以从这些交叉特征中分别学习 “看过电影 A” 的 representation 、“年龄等于20” 的 representation，最终泛化到这个未被观察到的交叉特征。

9.ALS优化算法

　　FM 的目标函数最优化可以直接采用随机梯度下降 SGD 算法求解，但是采用 SGD 有个严重的问题：需要选择一个合适的学习率。

学习率必须足够大，从而使得 SGD 能够尽快的收敛。学习率太小则收敛速度太慢。
学习率必须足够小，从而使得梯度下降的方向尽可能朝着极小值的方向。由于 SGD 计算的梯度是真实梯度的估计值，引入了噪音。较大的学习率会放大噪音的影响，使得前进的方向不再是极小值的方向。

　　论文提出了一种新的交替最小二乘 alternating least square:ALS 算法来求解 FM 目标函数的最优化问题。与 SGD 相比ALS 优点在于无需设定学习率，因此调参过程更简单。

四、FFM（Field-aware Factorization Machine）

1.考虑一组特征：“性别、年龄、城市”。为简化讨论，假设：“年龄”取值集合为 [18,19,20]， “城市” 取值集合为 [北京,上海,广州,深圳] 。把离散特征 one-hot 编码，设各 binary 特征分别记作：male,female,age18,age19,age20,bj,sh,gz,sz， y 表示样本标签（-1 表示不感兴趣，+1 表示感兴趣）。

记作：

技术图片

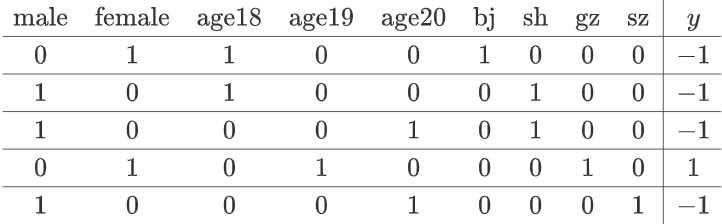
　　POLY2模型为：$\hat{y}(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\sum_{i=1}^{K} \sum_{j=i+1}^{K} w_{i, j} \times x_{i} \times x_{j}$，参数个数为$O(K^2)$，计算复杂度为$O(K^2)$

　　FM模型为：$\hat{y}(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\sum_{i=1}^{K} \sum_{j=i+1}^{K} \hat{w}_{i, j} \times x_{i} \times x_{j}$

　　$\hat{w}_{i, j}=<\overrightarrow{\mathbf{v}}_{i}, \overrightarrow{\mathbf{v}}_{j}>=\sum_{l=1}^{d} v_{i, l} \times v_{j, l}$，参数个数为$O(K \times d)$，计算复杂度为$O(K \times d)$

　　FM要优于POLY2，原因是：交叉特征非零的样本过于稀疏使得无法很好的估计$w_{i,j}$；但是在FM中，交叉特征的参数可以从很多其他交叉特征中学习，使得参数估计更准确。如：交叉特征$(male=1,age19=1)$从未出现过，因此在POLY2模型中参数$w_{male=1,age19=1}$根本无法学习。而在FM模型中$male=1$的representation向量可以从以下交叉特征的样本中学习：$(male=1,age18=1)，(male=1,age20=1)，(male=1,sh=1)，(male=1,sz=1)$，$age19=1$的representation向量可以从交叉特征$(age19=1,gz=1)$的样本中学习。

　　另外，FM还可以泛化到没有见过的交叉特征。如：交叉特征$(male=1,age19=1)$从未在训练样本中出现过，但是在预测阶段FM模型能够较好的预测该交叉特征的测试样本。

2.在FM模型中，每个特征的representation向量只有一个。如：计算$\hat{w}_{male=1,age=18}$，$\hat{w}_{male=1,age=20}$，$\hat{w}_{male=1,sh=1}$用到的是同一个向量$\overrightarrow{\mathbf{v}}_{\text {male }}=1$，论文《Field-aware Factorization Machines for CTR Prediction》提出的 FFM 算法认为：$age=18$ 和 $sh=1$ 之间的区别，远远大于 $age=18$ 和 $age=20$ 之间的区别。

　　因此，FFM 算法将特征划分为不同的域field。其中：

特征$male=1,female=1$属于性别域 gender field 。
特征$age18=1,age19=1,age20=1$属于年龄域 age field 。
特征$bj=1,sh=1,gz=1,sz=1$属于城市域 city field 。

FFM中每个特征的representation向量有多个，用于捕捉该特征在不同field中的含义：

如：特征$male=1$具有两个representation向量：

当用于计算age field域的交叉特征时，采用${\overrightarrow{\mathbf{V}} \mathrm{male}=1,age}$
当用于计算city field域的交叉特征时，采用${\overrightarrow{\mathbf{V}} \mathrm{male}=1,city}$

3.FFM模型

FFM模型用数学语言描述为：

$\begin{aligned} \hat{y}(\overrightarrow{\mathbf{x}})=w_{0} &+\sum_{i=1}^{K} w_{i} \times x_{i}+\sum_{i=1}^{K} \sum_{j=i+1}^{K} \hat{w}_{i, j} \times x_{i} \times x_{j} \\ & \hat{w}_{i, j}=<\overrightarrow{\mathbf{v}}_{i, f_{j}}, \overrightarrow{\mathbf{v}}_{j, f_{i}}>=\sum_{l=1}^{d} v_{i, f_{j} l} \times v_{j, f_{i}, l} \end{aligned}$

其中，$f_i$表示第$i$个特征所属的field，一共有F个field（1<=F<=K），参数数量为$O(K \times d \times F)$，计算复杂度为$O(\bar{K} ^2 \times d)$，其中$\bar{K}$是样本中平均非零特征数。

4.和FM相比，通常FFM中representation向量的维度要低的多。即$d_{FFM} \ll d_{FM}$

5.FFM每个representation向量的学习只需要特定field中的样本。如：学习$\overrightarrow{\mathbf{v}}_{\text {male}}=1,age$时，只需要考虑交叉特征$(male=1,age18=1),(male=1,age20=1)$的样本，而不需要考虑交叉特征$(male=1,sh=1),(male=1,sz=1)$的样本。

6.和FM相比，FFM模型也可以用于求解分类问题（预测各评级的概率），也可以用于求解回归问题（预测各评分大小）。

对于回归问题，其损失函数为MSE 均方误差：

$\begin{aligned} \phi(\overrightarrow{\mathbf{x}})=& w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\sum_{i=1}^{K} \sum_{j=i+1}^{K} \hat{w}_{i, j} \times x_{i} \times x_{j} \\ \mathcal{L}=& \sum_{(\vec{x}, y) \in \mathbb{S}}(\phi(\overrightarrow{\mathbf{x}})-y)^{2}+\sum_{\theta \in \Theta} \frac{1}{2} \lambda_{\theta} \times \theta^{2} \end{aligned}$

对于二分类问题（分类标签为 -1,+1 ），其损失函数为交叉熵：

$\phi(\overrightarrow{\mathbf{x}})=w_{0}+\sum_{i=1}^{K} w_{i} \times x_{i}+\frac{1}{2} \sum_{l=1}^{d}\left(\left(\sum_{i=1}^{K} v_{i, l} \times x_{i}\right)^{2}-\sum_{i=1}^{K} v_{i, l}^{2} \times x_{i}^{2}\right)$
$p(\hat{y}=y | \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (-y \phi(\overrightarrow{\mathbf{x}}))}$
$\mathcal{L}=\left(\sum_{(\vec{x}, y) \in \mathbb{S}} \log (1+\exp (-y \phi(\vec{x})))\right)+\sum_{\theta \in \Theta} \lambda_{\theta} \times \frac{1}{2} \theta^{2}$

7.FFM模型采用随机梯度下降算法来求解，使用AdaGrad优化算法。在每个迭代步随机采样一个样本$(\overrightarrow{x},y)$来更新参数，则L退化为：

$\mathcal{L}=\log (1+\exp (-y \phi(\overrightarrow{\mathbf{x}})))+\sum_{\theta \in \Theta} \lambda_{\theta} \times \frac{1}{2} \theta^{2}$

8.field分配

FFM 模型需要为每个特征分配一个 field 。

（1）离散型特征 categorical ：通常对离散型特征进行 one-hot 编码，编码后的所有二元特征都属于同一个 field 。

（2）数值型特征 numuerical：数值型特征有两种处理方式：

　　a.不做任何处理，简单的每个特征分配一个field 。此时$F=K$ ， FFM 退化为 POLY2 模型。

　　b.数值特征离散化之后，按照离散型特征分配 field 。论文推荐采用这种方式，缺点是： 难以确定合适的离散化方式。如：多少个分桶？桶的边界如何确定？ 离散化会丢失一些信息。

（3）离散集合特征categorical set（论文中也称作 single-field 特征）：所有特征都属于同一个field，此时$F=1$ ， FFM 退化为 FM 模型。

　　如 NLP 情感分类任务中，特征就是单词序列。如果对整个sentence 赋一个field，则没有任何意义。如果对每个word 赋一个 field，则等于词典大小，计算复杂度无法接受。

9.FFM应用场景：

数据集包含离散特征，且这些离散特征经过one-hot 编码。
经过编码后的数据集应该足够稀疏，否则 FFM 无法获取较大收益（相对于 FM ）。
不应该在连续特征的数据集上应用 FFM，此时最好使用 FM 。

五、GBDT+LR模型

1.模型来自论文：《Practical Lessons from Predicting Clicks on Ads at Facebook》

该模型利用 GBDT 作为特征抽取器来抽取特征、利用 LR 作为分类器来执行分类预测。

技术图片

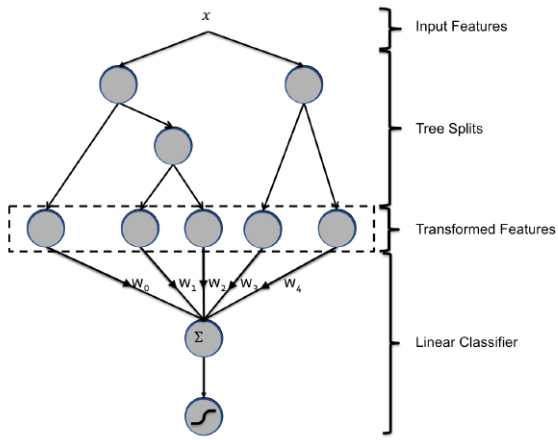
实验结果表明：GBDT-LR 比单独的 GBDT 模型，或者单独的 LR 模型都要好。

2.传统的搜索广告根据用户query 来检索候选广告，检索依据是：广告是否显式的或隐式的匹配用户 query 。而 Facebook 中的广告不是和用户 query 关联，而是和广告主指定的人群定向（如：年龄、性别、城市等统计特性，体育、财经、游戏等兴趣特性）相关联。这使得每个用户能够匹配大量的候选广告。

　　如果每次用户的广告请求都对这些候选广告做预测，则时间成本太高（广告检索有时间约束，时间太长则不可接受）。因此 Facebook 构建了一组分类器：

前期的分类器比较简单，处理候选广告多，计算成本低，同时预测准确率较差。
后期的分类器比较复杂，处理候选广告少，计算成本高，同时预测准确率较好。
每个分类器都将它们预测的低 pCTR 广告截断，从而降低下游分类器的处理数据量。

　　通过这种分类器级联的方式层层过滤，最终每个用户只需要对少量广告的点击率进行预测。本论文关注的是最后一个分类器，它为最终候选广告集合生成点击率预估

3.评估指标

（1）论文提出归一化熵Normalized entropy：NE来评估模型。

假设样本集合有N个样本，样本集合的经验CTR为$\bar{p}$（它对于所有正类样本数量除以总样本数量）。

假设第$i$个样本预测为正类的概率为$p_i$，其真实标签为$y \in \{-1,+1\}$。

定义背景点击率background CTR为样本集合经验CTR，它的熵定义为背景熵：$H_{bg}=-plogp-(1-p)log(1-p)$。背景熵衡量了样本集合的类别不平衡程度，也间接的衡量了样本集合的预测难度。类别越不均衡预测难度越简单。因为只需要将所有样本预测为最大的类别即可取得非常高的准确率。
定义模型在样本集合熵的损失函数为：$\mathcal{L}=-\sum_{i=1}^{N}\left(\frac{1+y_{i}}{2} \log p_{i}+\frac{1-y_{i}}{2} \log \left(1-p_{i}\right)\right)$，每个样本的损失为交叉熵。
定义归一化熵NE为：模型在所有样本的平均损失函数除以背景熵。$NE=\frac{\mathcal{L} / N}{H_{bg}}$，分子需要除以$N$是为了剔除样本集合大小的影响。NE相对损失函数的优势在于：NE考虑了样本集预测的难易程度。在平均损失相同的情况下，样本集越不平衡则越容易预测，此时NE越低。

（2）AUC也是评估模型能力的一个很好的指标，但是AUC反应的模型对样本的排序能力：auc=0.8表示80%的情况下，模型将正样本预测为正类的概率大于模型将负样本预测为正类的概率。

　　假设我们预估的pCTR $p_i$是有偏的（相比较经验CTR），此时我们需要乘以一个系数$\gamma$来校准calibration。

在校准前后，模型的AUC保持不变，因为对所有正负样本的pCTR乘以一个系数不改变它们的排序rank。
在校准前后，模型的NE得到改善。因为校准后的pCTR分布于样本的标签分布距离更近。

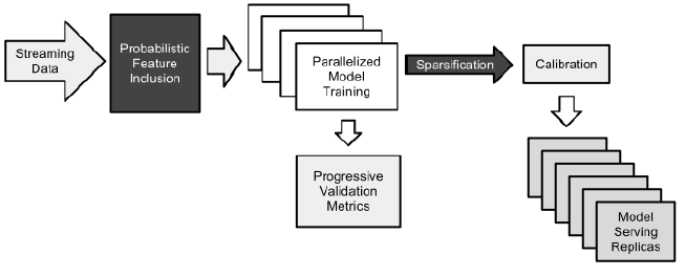
4.GBDT特征提取

有两种最简单的特征转换方式：

连续特征离散化：将连续特征的取值映射到一个个分散的分桶里，从而离散化。这里桶的数量和边界难以确定，通常有两种方法： a.通过人工根据经验来设定分桶规则；b.利用后续的分类器来显式的学习这个非线性映射，从而学习出有意义的分桶数量和边界。
离散特征交叉：类似 FM 模型采用二路特征交叉（或者更高阶）来学习高阶非线性特征。对于连续特征可以先离散化之后再执行特征交叉，如 kd 树就是典型的代表。 Boosted decisition tree:BDT 就是结合了上述两种方式的一个强大的特征提取器。

　　对于 BDT，我们将每棵子树视为一个离散特征，其叶结点的编号为特征的取值并执行 one-hot 编码。假设 BDT 有两棵子树，第一棵有 3 个叶结点，第二棵有2 个叶结点。则样本提取后有两个特征：第一个特征取值为 {1,2,3}，第二个特征取值为 {1,2} 。假设某个样本被划分到第一棵子树的叶结点 2，被划分到第二棵子树的叶结点 1，则它被转换后的特征为：[0,1,0,1,0]。其中：前三项对应于第一个离散特征的 one-hot，后两项对应于第二个离散特征的 one-hot 。

技术图片

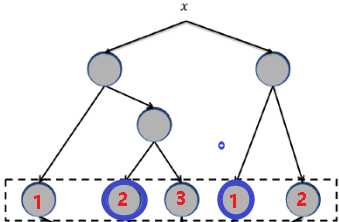
　　论文采用梯度提升树 Gradient Boosting Machine:GBM 来训练每棵子树，因此这种特征提取方式可以视为基于决策树的有监督特征编码：

它将一组实值向量 real-valued vector 转换为一组二元向量 binary-valued vector 。
每棵子树从根节点到叶节点的遍历表示某些特征转换规则。
在转换后的二元向量上拟合线性分类器本质上是学习每个规则的权重。

实验结果表明：采用 GBDT-LR 的模型相比于单独的 GBDT 提升了 3.4%。

技术图片

5.数据新鲜度freshness

　　CTR 预估模型通常部署在数据分布随时间变化的动态环境中。训练数据和测试数据的时间距离越近，二者的数据分布差距越小，效果也越好。

　　论文用某一天的样本数据训练一个模型，然后用该模型评估当天、一天后、两天后、... 六天后的测试数据。结果表明：模型需要每天根据最新的样本进行重新训练。与每周训练一个模型相比，每天训练一个模型可以提升模型效果大约 1%（以 NE 为指标）。

技术图片

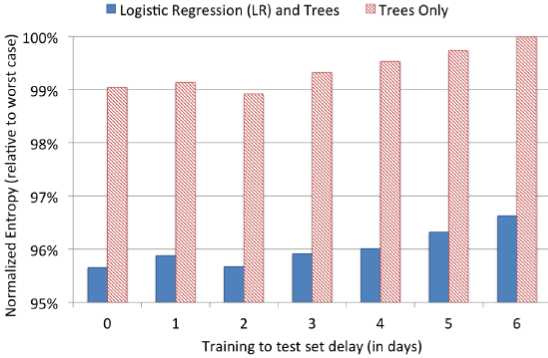
　　考虑数据新鲜度，我们需要用最新的样本更新模型。有两种更新策略：

每天用最新的数据重新训练模型。当模型比较大时，可能要花费几个小时甚至24个小时以上来训练。
每天或者每隔几天来训练特征提取器 BDT ，但是用最新的数据在线训练 LR 线性分类器。

6.学习率

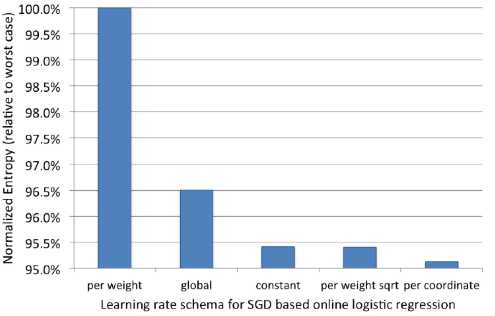
当通过mini-batch 梯度下降法来训练在线 LR 分类器时，学习率的设定非常关键。有几种学习率设定方式：

（1）per-coordinate 基于特征的学习率

在第t次迭代特征i的学习率为：$\eta_{t, i}=\frac{\alpha}{\beta+\sqrt{\sum_{j=1}^{t}\left(\overrightarrow{\mathbf{g}}_{j}\right)_{i}^{2}}}$，其中：$\alpha , \beta$为模型的超参数；$\overrightarrow{\mathbf{g}}_{j}$为第$j$词迭代的梯度在特征$i$的分量。

特征$i$的梯度越大，说明该特征方向波动较大，则学习率越小，学习速度放慢。
特征$i$的梯度越小，说明该特征方向波动较小，则学习率越大，学习速度加快。

（2）per-weight 维度加权学习率

在第$t$次迭代特征$i$的学习率为：$\eta_{t, i}=\frac{\alpha}{n_{t,i}}$，其中：$\alpha$为模型的超参数，$n_{t,i}$为截止到第$t$次迭代特征$i$上有取值的所有样本数量。在特征上有取值表示：one-hot之后的取值为1。

对于广义线性模型：$\hat{y}=f(z),z=\sum _{i=1} ^ n x_i \times w_i$

设损失函数为$L(y,\hat{y})$，则有：

$\begin{aligned} \frac{d L}{d w_{i}}=& \frac{d L}{d \hat{y}} \times \frac{d \hat{y}}{d z} \times x_{i} \\ \text { update: } w_{i} & \leftarrow w_{i}-\eta_{t, i} \times \frac{d L}{d w_{i}} \end{aligned}$

　　因此可以看到，对于罕见特征由于大多数情况下特征取值$x_i=0$ ，因此特征权重$w_i$几乎很难有更新的机会。

特征$i$上有取值的样本越多，则可供学习的样本也多，则学习率越小，学习速度放慢。
特征$i$上有取值的样本越少，则可用学习的样本也少，则学习率越大，学习速度加快。

（3）per-weight square root 基于权重开方的学习率

在第$t$次迭代所有特征的学习率为：$\eta_{t, i}=\frac{\alpha}{\sqrt{n_{t,i}}}$

（4）global 全局学习率

在第$t$次迭代所有特征的学习率为：$\eta_{t, i}=\frac{\alpha}{\sqrt{t}}$

（5）constant 常量学习率

在第$t$次迭代所有特征的学习率为：$\eta_{t, i}=\alpha$

论文验证了这几种学习率的效果，其中超参数通过grid search 来得到。

技术图片

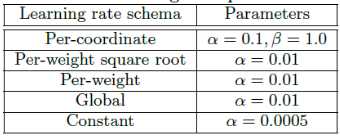
结果表明：per-coordinate 方法获得最好的表现，而 per-weight 效果最差。

全局学习率表现不佳，其主要原因是：每个特征上训练样本数量不平衡。一些常见特征上（如：“是否男性” 特征）的样本数量较多，而另一些罕见特征（如：“是否明星” ）上的样本数量较少。在全局学习率策略下，罕见特征学习率太快降低到很小的值，使得最优化难以收敛到最优点。
虽然 per-weight 策略解决了该问题，但是它仍然表现不佳。主要原因是：虽然它对罕见特征的学习率控制较好，但是它对常见特征的学习率控制较差。它太快的降低了常见特征的学习率到一个很小的值，在算法收敛到最优点之前训练就过早终止了。

技术图片

7.在线训练框架

（1）在线训练框架最重要的是为模型提供在线学习的标注样本。点击行为比较好标记，但是“不点击”行为难以标记。因为广告并没有一个“不点击”按钮来获取不点击的信息。因此，如果一个曝光在一个时间窗内未发生点击行为，则我们标记该次曝光是未点击的。之所以要设定一个时间窗，是因为广告曝光和用户点击之间存在时间差。

　　给定一个曝光，我们需要等待一段时间来确认它是否被用户点击。如果等待时间内收到了曝光的点击信息，则该曝光标记为正样本。如果等待时间内未收到曝光的点击信息，则该曝光标记为负样本。

　　等待的时长需要精心选择：如果时间太长则实时训练数据延迟较大，数据 freshness 较差。同时，为了存储更长时间的曝光数据内存代价也较高。如果时间太短则因为没有等到点击信息回传，部分正样本被误判为负样本。这会导致实时样本集的经验 CTR 比真实 CTR 偏低。这种经验CTR 的偏差也可以检测并矫正。因此，需要在数据的 freshness 和点击覆盖率（能匹配上曝光的点击的数量占总点击数量之比）之间平衡。通过挑选合适的时长，可以降低经验的 CTR 偏差到百分之1以下，同时内存代价也可以接受。

（2）Facebook 在线训练框架

技术图片

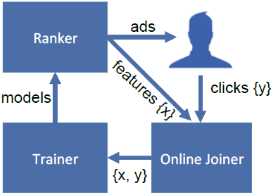
a.用户浏览 Facebook 时向 Ranker 模块发送一个广告请求，请求中包含 request ID 。

b.Ranker 模块根据在线模型的预测结果，向用户返回一个广告，同时在曝光实时数据流中增加一条曝光日志。如果用户点击广告，则前端打点系统上报点击事件，在后台点击实时数据流中增加一条点击日志。

c.通过 Oneline Joiner 模块实时获取最近一个时间窗的曝光、点击日志，并拼接样本特征来构造训练集。 d.Trainer 模块根据构造的训练集执行在线训练，训练好的模型部署到线上供 Ranker 模块使用。

这会形成一个数据闭环，使得模型能够捕捉到最新的数据分布。

（3）在线训练需要增加对实时训练数据的异常保护。

假设实时训练数据出现问题（如：前端打点上报出现异常、Online Joiner 工作异常等），导致大量的点击数据丢失。那么这批实时训练样本存在缺陷，它们的经验 CTR 非常低甚至为 0 。

如果模型去学习这样一批样本，则模型会被带偏：对任何测试样本，模型都会预测出非常低、甚至为零的点击率。根据广告点击价值 eCPM = BID x pCTR，一旦预估点击率 pCTR 为零则广告的 eCPM 为零。那么这些广告几乎没有竞争力，竞争失败也就得不到曝光机会。

因此需要增加实时训练数据的异常检测机制。如：一旦检测到实时训练数据的分布突然改变，则自动断开在线训练流程。

8.优化技巧

（1）子树规模

在 GBDT-LR 模型中，子树的数量越大模型表现越好，但是计算代价、内存代价越高。但是随着子树的增多，每增加一棵子树获得的效益是递减的。这就存在平衡：新增子树的代价和效益的平衡。

（2）特征数量

　　在 GBDT-LR 模型中，样本特征越大模型表现越好，但是计算代价、内存代价越高。但是随着特征的增多，尤其是无效特征的增多，每增加一个特征获得的效益是递减的。这就存在平衡：新增特征的代价和效益的平衡。

　　为衡量特征数量的影响，我们首先对特征重要性进行排序，然后考察 topK 重要性特征的效果。可以通过 Boosting Feature Importance 来衡量特征重要性。有三种度量方法（如 XGBoolst/LightGBM ）： a.weight：特征在所有子树中作为分裂点的总次数； b.gain：特征在所有子树中作为分裂点带来的损失函数降低总数； c.cover：特征在所有子树中作为分裂点包含的总样本数

（3）降采样

Facebook 每天的广告曝光量非常大。即使是每个小时，数据样本也可能上亿。在线学习需要对样本进行采样来降低数据量，从而提升训练速度。

有两种降采样技术：

a.均匀降采样：所有样本都以同一个概率$p_{sample}$来随机采样。

　　该方法容易实现，且采样后的样本分布和采样前保持不变。这样使得训练数据集的分布基本和线上保持一致。论文考察了几种采样率： 0.001,0.01,0.1,0.5,1 。结果表明：更多的数据带来更好的模型。但是采用 10% 的训练样本相对于全量样本仅仅损失了 1% 的预测能力（经过模型校准之后甚至没有降低），而训练代价降低一个量级。

b.负降采样：保留所有的正样本，仅负样本以概率$p_{sample}$来随机采样。

　　保留所有的正样本，仅负样本以概率来随机采样。该方法可以缓解类别不平衡问题。但是，采样后的样本分布和采样前不再相同，导致训练集的分布和线上不再保持一致。因此需要对模型进行校准。论文考察了几种采样率： 0.1,0.01,0.001,0.0001,... 。结果表明：最佳负采样率在 0.025 。

9.历史统计特征

模型中用到的特征分类两类：上下文特征和历史统计特征。

上下文特征：曝光广告的当前上下文信息。如：用户设备、用户所在页面的信息等等。
历史统计特征：广告的历史统计行为，或者用户的历史统计行为。如：广告的上周平均点击率，用户的历史平均点击率。

　　取 top K 重要性的特征，通过查看历史统计特征的占比来评估这两类特征的重要程度。结果表明：历史统计特征比上下文特征更重要。

10.模型校准calibration

模型校准分为两类：

模型预测能力不足导致的校准
训练数据分布和线上数据分布不一致导致的校准。

相比较第一类情况，第二类情况的校准系数偏离 1.0 更为严重，因此也更需要执行校准。

（1）给定样本集，假设模型预估的pCTR分别为$(\hat{y_1},...,\hat{y_N})$，则样本集的经验CTR为：$\overline{\mathrm{CTR}}=\frac{\sum_{i=1}^{N} \mathbb{I}\left(y_{i}=1\right)}{N}$

样本集的预估平均CTR为：$\overline{\mathrm{CTR}}_{pred}=\frac{\sum_{i=1}^{N}{\hat{y_i}}\left(y_{i}=1\right)}{N}$

定义校准系数为：预估平均CTR和经验CTR之比：$r a t i o=\frac{\overline{\mathrm{CTR}}_{p r e d}}{\overline{\mathrm{CTR}}}$

它衡量了模型预期点击次数和实际观察到的点击次数之比，它的值与 1 的差异越小，则模型的表现越好。假设模型预估的结果为$\hat {y}$ $，则校准后的预估结果为：$\hat{y}_{n e w}=\frac{\hat{y}}{r a t i o}$$

（2）负降采样可以加快训练速度，改善模型能力。但是负采样中的训练数据分布和线上数据分布不一致，因此必须对模型进行校准。

假设采样之前样本集的平均 CTR 为 0.1% 。当执行采样率为 0.01 的负降采样之后，由于正样本数量不变、负样本数量降低到之前的 0.01 ，因此采样后的样本集的平均 CTR 为 10% 。此时需要校准模型，使得模型的预估平均 CTR 尽可能与线上的平均 CTR 一致。假设模型预估的结果为$\hat {y}$ ，则校准后的预估结果为：

$\hat { y} _{new} = \frac{\hat {y}}{\hat {y} + (1-\hat {y}) / s}$，其中$s$为负采样比例。