标签:建议 splay 思考 ios 设立 大数 旋转 世界 变量
学着zkw突然回来整理平衡树
平衡树呢,是一种比较毒瘤的数据结构,
首先,其种类非常多,实现原理也各有差异,各有千秋,
而且其应用也非常广泛,
之前看见_rqy说不会线段树然后敲了一个平衡树A掉题目
所以我将分类整理各类平衡树
说到Splay,第一次正式学习是在qbxt的晚自习,然而并没有听懂,最近回来补发现并不难
因为平衡树主要操作无非分割和旋转两类整理操作,Splay是旋转操作,
所以Splay的主要操作核心就在于交换节点之间的关系,那么懂了思路以后,就全是模拟啦...
事实上学了Splay,旋转Treap是很简单的东西
一种非常广泛的数据结构,主要的操作就是转...
Splay的操作较简单,主要是模拟,
唯一的前置知识好像就是就是二叉搜索树\(BST\)(\(binary\ search\ tree\))
具有以下特性:
显然是一棵二叉树,
每个节点有一个权值\(val\),
对于每个节点\(k\),要么其左子树为空,否则其左子树的所有元素节点权值都小于\(val[k]\),
对于其右子树,要求其中权值全部大于\(val[k]\),
如果整棵树中有几个节点权值相等,那么将这个元素对应的节点多开一个域\(sum\),表示这个权值的元素的个数
树中所有子树全是\(BST\)
这样一来,形态大致如下:
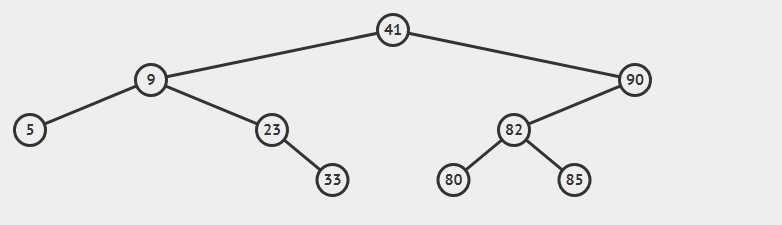
我们为什么要设立这样一个建立结构的规则呢?
显然这样非常适合数的查找,基本上就是二分的思路,无论是访问第\(k\)小值,还是访问权值为\(v\)的节点,都可以快速地实现目标,插入也是如此
具体步骤(比如找权值为\(v\)的元素):
从根节点开始寻找:
对于当前节点\(k\),如果现在\(v = val[k]\),
否则,如果当前值较小,说明目标值一定在左子树,查找左儿子,否则去查找右儿子,
重复2-3步,直到出现以下两种状况:
在查找过程中如步骤2,找到节点,完成查找,
直到找到最下方的空节点,也没有找到目标节点,说明这个节点并不存在
(查询操作一般不会这样的)
p.s. 对于插入操作,如果找到第二种情况的空节点,那么说明可以直接插入这个新节点,毕竟之前没有这个节点,新建就完了
这里注意,我们处理这些信息根本不用递归,只需要写个函数然后在函数之内跑循环就完了,这样更加高效
这就是\(BST\)处理元素的主要原理,步骤
可以发现这样类似于二分的方法是非常高效的,可以方便地维护出数列中与大小关系有关的数据
比如说:
求比\(v\)小的最大数(前驱)
求区间内第\(k\)大的数(并不)
注意区间求值是树套树的操作,不是\(BST\)的操作
那么在没接触Splay的情况下,我们来看一看完全不需要Splay的一些操作及函数实现:
int ch[N][2],f[N],size[N],sum[N],val[N];
int rt,cnt;我们一般采用动态开点的操作来进行元素插入,说的通俗就是随着用随着开
这里变量\(cnt\)就是这样一个作用,开点的时候:
++cnt;
nd[cnt]=...;rt存的是当前\(BST\)的根
\(ch[k][0/1]\)储存的是每个节点的左右儿子,\(ch[k][0]\)为左,\(ch[k][1]\)为右,
\(f[k]\)储存的则是节点父亲,\(f[rt]=0\),
\(val[k]\)存的是\(k\)节点的值,
\(size[k]\)存以节点\(k\)为根的子树的大小,
\(sum[k]\)存元素\(k\)出现的次数,就是序列中有几个值为\(val[k]\)的元素
用于更新节点信息,具体作用其实就是维护子树大小,节点的关系不改变
inline void update(ci x){
if(!x) return ;
size[x]=sum[x];
if(ch[x][0]) size[x]+=size[ch[x][0]];
if(ch[x][1]) size[x]+=size[ch[x][1]];
}翻译:
这里注意这个函数的使用,\(update\)操作一定要先对子节点再对父节点,这样才能保证正确性,
因为越是深度小的节点,其信息就越是从子节点合并上来的,如果先更新父节点,父节点的信息很可能没有被"最新"子节点信息更新,反而被未更新的"老"子节点更新,在信息访问的时候会爆炸,实为下策
如果先维护子节点,那么其所有祖宗节点的更新都有了保障,因为其使用的子节点信息全部是更新过的,
主要实现思想在上面了,
代码给出,
inline void insert(ci x){
if(!rt){
cnt++;
ch[cnt][0]=ch[cnt][1]=f[cnt]=0;
rt=cnt;
size[cnt]=sum[cnt]=1;
val[cnt]=x;
return ;
}int now=rt,fa=0;
while(1){
if(val[now]==x){
sum[now]++;
update(now);
update(fa);
return ;
}fa=now;
now=ch[now][val[now]<x];
if(!now){
cnt++;
ch[cnt][0]=ch[cnt][1]=0;
f[cnt]=fa;
sum[cnt]=size[cnt]=1;
ch[fa][val[fa]<x]=cnt;
val[cnt]=x;
update(fa);
return ;
}
}
}翻译:
这里有一点可能很迷惑,就是为什么在建立节点更新的时候不用一步步递归把上面的所有节点更新呢?
上面讲到,每个非叶节点的子树大小都是由子节点维护上来的,那么只要子节点是新的,父节点的维护就一定不会出错,只是时间可能晚一些
也就是说,对于操作更新的子树大小的信息,我们完全可以将离当前节点很远的祖宗节点暂时放弃修改,等着以后在遍历到这个节点是顺便进行更新,既不会导致错误,也提升了代码效率,
但前提就是先维护子节点
对于新建节点的细节,看看代码,主要熟悉流程就好了,主要就是模拟
就是模拟,找小往左找大往右,
inline int find(ci x){
int k=0,now=rt;
while(1){
if(x<val[now]) now=ch[now][0];
else{
k+=(ch[now][0]?size[ch[now][0]]:0);
if(val[now]==x) return k+1;
k+=sum[now];
now=ch[now][1];
}
}
}注意处理好儿子的存在性问题
inline int find_kth(int x){
int now=rt;
while(1){
if(ch[now][0]&&x<=size[ch[now][0]])
now=ch[now][0];
else{
int temp=(ch[now][0]?size[ch[now][0]]:0)+sum[now];
if(x<=temp) return val[now];
x-=temp;
now=ch[now][1];
}
}
}对于当前子树,要找第\(k\)小元素
从左子树找,就从左子树找其中的\(k\)小元素,从右子树找就找右子树中的第\(k-size[左儿子]\)小的元素
因为只要在右子树中寻找,这个元素就一定是大于左子树中所有元素的,其元素排名一定是大于左子树大小的
就是查询比某个数小的最大数,或是比其大的最小数,
懒得写基本实现了
要知道的就只是个思路就行,主要就是先找目标元素对应的节点,如果查前驱就往左边找,找左边最靠右的
感性理解下...
(这里不一定是左子树,万一要查询的元素是叶节点呢?)
查后继就往右边找,同理不再赘述,
//加上某种操作,让查询的元素成为根(不存在就先插入,完成查询再删除)...val[rt]存的即为查询的值
inline int pre(){
int now=ch[rt][0];
while(ch[now][1]) now=ch[now][1];
return now;
}
inline int next(){
int now=ch[rt][1];
while(ch[now][0]) now=ch[now][0];
return now;
}因为普通\(BST\)虽是可以实现,但是实现方法与下面要讲的Splay删除相比,并不精彩,
而且好像并没有必要掌握\(BST\)的删除操作...
作为一棵平衡树,Splay显然也是一棵\(BST\),但是显然有不同,
Splay等平衡树是基于\(BST\)的优化
考虑\(BST\)有什么可以优化的:
众所周知,\(BST\)用的是二分的相关思想,所维护的节点关系就只有"左小右大"
因为只维护一个性质,所以其结构并不唯一,
比如下面的这棵\(BST\)
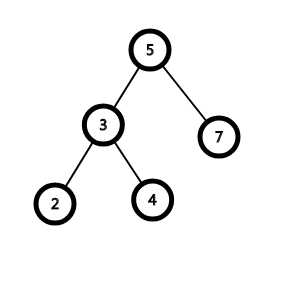
显然也可以是这样:
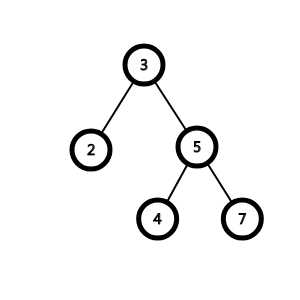
所以,但凡数据有序,就会这样:
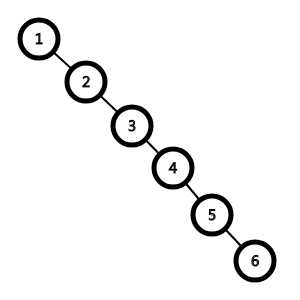
也就是说,原本可以二分的树现在变成了一条链,只能\(O(n^2)\)暴力,大大降低效率
这样一来,树的形态似乎完全取决于插入的顺序,数据又取决于人...
树的形态又决定了代码的效率,因为我们知道一棵树中一定是拥有两个子节点的节点个数越多越好,
这样才能高效地二分,
对于链(或者结构凡是像链),就只能暴力查找,失去了\(BST\)原本的优良性质
所以说,只要造数据的想,就可以随时随地卡死你,就算是把暴力分给你你也拿不了多少,
那么我们能不能改变这种现状,让\(BST\)的结构不再根据输入而定呢?
其中一种操作就是今天要介绍的--Splay(伸展)
Splay的汉语释义是"伸展",显然,我们不能一巴掌把一棵\(BST\)物理伸展开来,
我们考虑旋转操作,
就是我们通过花式旋转,把\(BST\)伸展,
先看看怎么旋转,再去看怎么通过新定义的旋转实现树的伸展,
我们现在“发明”一个函数,传唯一的参数\(x\),表示让节点\(x\)旋转到其父亲的位置,当然树的结构改变,但是树作为\(BST\)的性质没有改变,
我们根据实际情况来判断到底如何实现
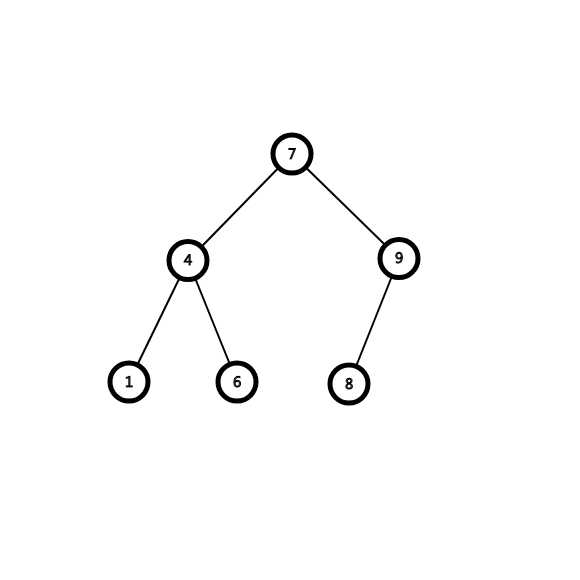
加入我们要让节点4旋转到其父亲位置-7的位置上去,
在旋转的同时,我们需要考虑节点关系的过继问题,
考虑下面几种策略:
按照这种思路维护出来是这样:
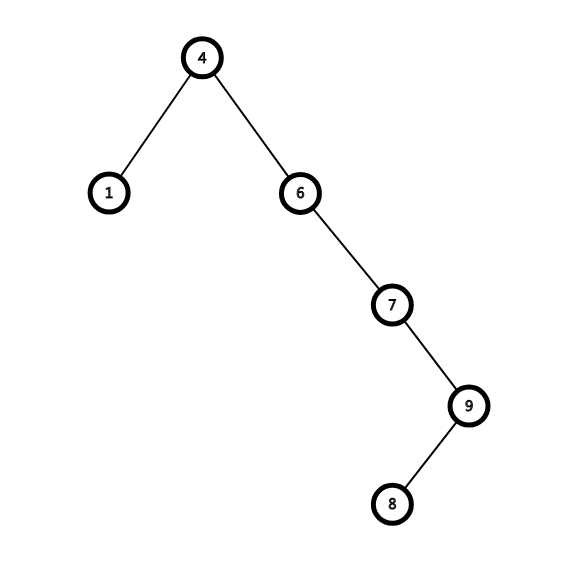
直接变成链...
如果这样操作的话,节点4的位置倒是很好操作,但是其子树中的节点关系不好维护,如果将节点7归到节点6的右子树中去,实在难有结论,
不难看出这种情况就算很优秀,其子树中关系维护也真的不好写,
同时我们发现,上面这种维护实质确实是"伸展"了这棵\(BST\),但是这种操作实际上是把树往链的方向展开,
因为在旋转的同时,我们只是将4节点的位置进行调换,将其它节点关系丢给子树去处理,这使得本来就属于节点4的子树和节点7及其整棵右子树一起为树的高度贡献了不可或缺的力量...
这里原本节点7的左子树是节点4为根的树,但是旋转以后我们发现节点7的左子树根本不见了,因为我根本没有考虑节点7的左子树这个空间该怎么去用,导致了树中位置的浪费,进而导致链的形成
一开始我们就提到,链的形态是并不利于\(BST\)操作的,所以这种方法并不可取,
我们所说的"Splay伸展"是为了尽量减少树的高度,为了维护其\(BST\)操作较方便的形态,
我们不妨考虑这样的方法:
维护完像这样:
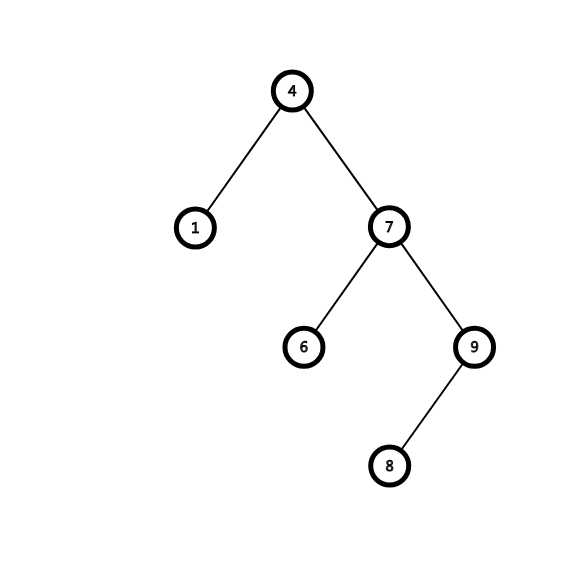
这样一来显然这棵树显得满多了,起码比之前链的形态好很多,
然而上面概括的步骤仅是对于当前节点是父节点的左儿子的情况,
同理,对于右边的节点要旋转到其父亲的位置,只需要把目标节点的左子树接到父节点的右子树上,再将父节点的整棵树接到目标节点的左子树就好了
于是我们有了旋转操作\(_{的思想}\)
有了上面的思路,只需要写并不繁琐的模拟代码就可以实现辣!
先写下\(get\)函数,判断目标节点是哪个儿子
inline int get(ci x){
return ch[f[x]][1]==x;
}精简不失优美...太棒了这代码...
inline void rotate(ci x){
int old_root=f[x],old_fa=f[f[x]],opr=get(x);
ch[old_root][opr]=ch[x][opr^1];
f[ch[old_root][opr]]=old_root;
ch[x][opr^1]=old_root;
f[old_root]=x;
f[x]=old_fa;
if(old_fa) ch[old_fa][ch[old_fa][1]==old_root]=x;
update(old_root);
update(x);
}因为在处理节点关系的时候会非常乱,所以先开变量储存原来节点的关系,就是存一下原来谁是爹,谁是爷爷什么的...
最后进行更新,还是依据儿子优先法则
不得不说一句,Tarjan大佬发明的数据结构操作就是强,连儿子身份的判断与运算也这样简洁,来去自如!
我们知道一个非根节点,它不是左儿子就是右儿子
那么我们规定,这个"左儿子","右儿子"这些称呼叫做这个节点的身份
这里的\(splay\)指的就是伸展函数了,目的就是伸展,但是其主要目的是把目标节点旋转到根节点
而且在Splay中,几乎处处可见\(splay\)函数的身影,就是因为Splay实在频繁的更新结构的状态下维护形态的优美的
具体思路:
如果我们要让最底部的节点升到根节点位置,
考虑现在有一条链(当然在Splay里因为频繁维护并不会出现长度非常长的链的情况):
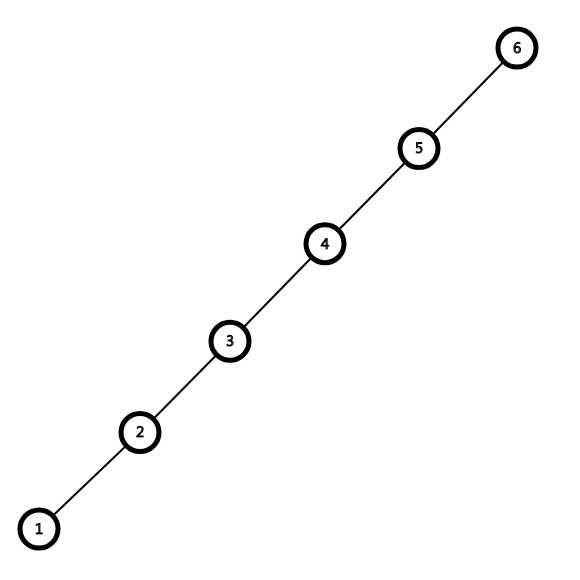
我们要让\(BST\)维护树的优美性质,显然我们需要让\(BST\)盘区折叠,现在我们要\(splay\)节点1旋转到根节点的位置,
在旋转之前,我们先思考一下,如何转才能让\(BST\)有一个多叉的结构,
不难看出,"多叉"转化为图中的信息,就是节点的儿子尽可能的多,
但是如果我们仅以将节点1旋转为根节点为目的,这样旋转:
while(rt!=1){
rotate(1);
}旋转完成后是这种东西:
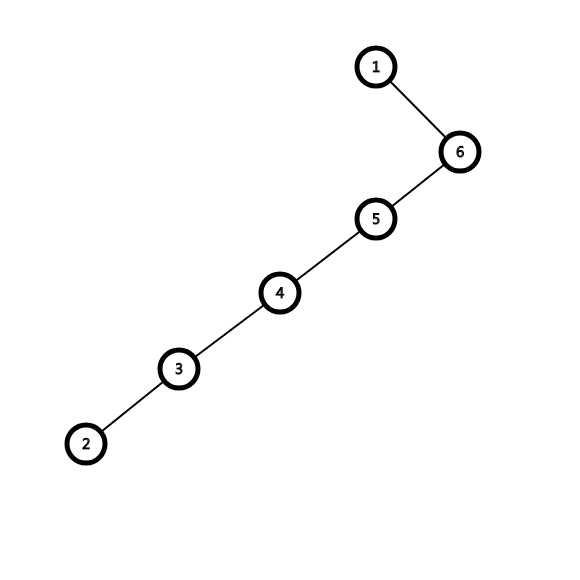
这并不"优美",如果这样那\(splay\)的工作就仅是调整了节点的位置,并没有对结构进行优化
那么为了使树的就够更加盘区折叠,我们这样操作:
对于当前节点,如果其身份和其父节点的身份不一致,说明这棵树本身就比较优美,可以直接对当前节点进行\(rotate\)
如果其节点身份同其父节点身份相同,那么我们起码可以判断我们要操作的节点似乎形成了一个链状结构,
那么为了破坏这个链状结构,使其结构弯曲,
我们先对目标节点的父亲进行\(rotate\),这样就破坏了链的结构,
然后再对目标节点进行\(rotate\),
重复以上步骤直到目标节点为根节点.
伸展完成以后是这个亚子:
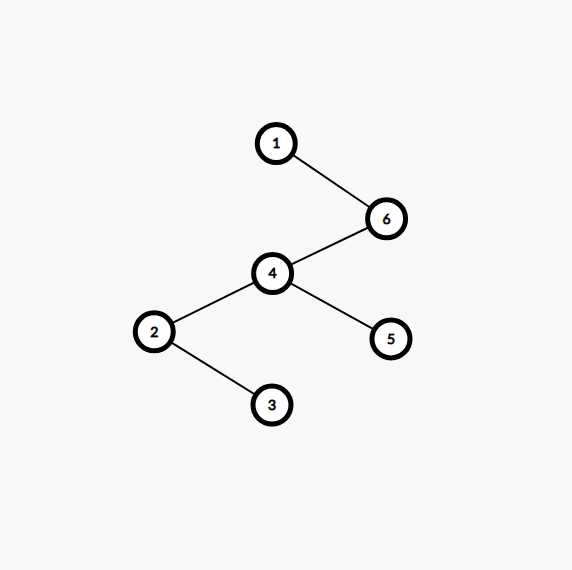
这样一来就好多了,
于是以上法则就是我们伸展\(BST\)的法则,然后自己模拟下就吼了~
当然建议自己多举几个例子找普遍规律.
代码贴出(很好理解)
inline void splay(int x){
for(int fa;fa=f[x];rotate(x))
if(f[fa])
rotate((get(x)==get(fa))?fa:x);
rt=x;
}这里\(for\)循环中\(fa=f[x]\)的用法是先赋值再判断,判断\(fa\)是否为0(节点的父亲是否存在)
于是,基于此,几乎所有函数我么都可以加一条\(splay\)函数,让当前操作的目标旋转为根节点,一来方便操作,二来优化了结构
这里指的删除指的不一定是元素删除,更多的是元素个数-1,元素消失只是元素个数为0这一特殊情况
当然前提是找到元素\(x\),我们可以顺便将其旋转到根节点,以便操作,
也就是说我们操作的时候,目标节点已经是根节点了,
然后暴力分情况讨论:
元素个数不为1,直接将元素个数-1后更新节点信息完事走人
如果个数为1,但是左右儿子都为空的话,也就是说,删除操作之后,整棵树就会变为空树,那么直接清零就行了,此时\(rt=0\)
如果个数为1,且只有一个儿子的话,显然自己删掉以后将儿子赋为根就好了
否则,就是最普遍的情况,
当前节点删了就没,而且还同时拥有左右儿子,这使得删除操作很难受,
我们采取暴力而简洁的方法:
把目标节点的前缀旋转做根,这个操作使得前缀与目标节点直接相连,同时前缀节点就是根节点了,此时目标节点一定是这棵树根节点的右儿子,
这样我们可以直接将目标节点删除以后,将目标节点的右儿子提上来当做根节点的右儿子,这样一来目标节点就没了
代码:
inline void del(ci x){
find(x); //其中含有splay操作,将目标节点转移到根的位置
if(sum[rt]>1){sum[rt]--;update(rt);return ;}
if(!ch[rt][0]&&!ch[rt][1]){clear(rt);rt=0;return ;}
if(!ch[rt][0]){
int old_root=rt;
rt=ch[rt][1];
f[rt]=0;
clear(old_root);
return ;
}
if(!ch[rt][1]){
int old_root=rt;
rt=ch[rt][0];
f[rt]=0;
clear(old_root);
return ;
}
int prev=pre(),old_root=rt;
splay(prev);
ch[rt][1]=ch[old_root][1];
f[ch[old_root][1]]=rt;
clear(old_root);
update(rt);
}同样需要保存原先节点的关系
以上就是所有Splay的操作函数
结合主函数看一下,主要看前驱后继的实现,
#include<iostream>
#include<cstdio>
#define ci const int &
using namespace std;
const int N=100005;
int n;
int ch[N][2],f[N],size[N],sum[N],val[N];
int rt,cnt;
inline void clear(ci x){
ch[x][0]=ch[x][1]=f[x]=val[x]=sum[x]=size[x]=0;
}
inline int get(ci x){
return ch[f[x]][1]==x;
}
inline void update(ci x){
if(!x) return ;
size[x]=sum[x];
if(ch[x][0]) size[x]+=size[ch[x][0]];
if(ch[x][1]) size[x]+=size[ch[x][1]];
}
inline void rotate(ci x){
int old_root=f[x],old_fa=f[f[x]],opr=get(x);
ch[old_root][opr]=ch[x][opr^1];
f[ch[old_root][opr]]=old_root;
ch[x][opr^1]=old_root;
f[old_root]=x;
f[x]=old_fa;
if(old_fa) ch[old_fa][ch[old_fa][1]==old_root]=x;
update(old_root);
update(x);
}
inline void splay(int x){
for(int fa;fa=f[x];rotate(x))
if(f[fa])
rotate((get(x)==get(fa))?fa:x);
rt=x;
}
inline void insert(ci x){
if(rt==0){
cnt++;
ch[cnt][0]=ch[cnt][1]=f[cnt]=0;
rt=cnt;
size[cnt]=sum[cnt]=1;
val[cnt]=x;
return ;
}int now=rt,fa=0;
while(1){
if(val[now]==x){
sum[now]++;
update(now);
update(fa);
splay(now);
return ;
}fa=now;
now=ch[now][val[now]<x];
if(now==0){
cnt++;
ch[cnt][0]=ch[cnt][1]=0;
f[cnt]=fa;
sum[cnt]=size[cnt]=1;
ch[fa][val[fa]<x]=cnt;
val[cnt]=x;
update(fa);
splay(cnt);
return ;
}
}
}
inline int find(ci x){
int k=0,now=rt;
while(1){
if(x<val[now]) now=ch[now][0];
else{
k+=(ch[now][0]?size[ch[now][0]]:0);
if(val[now]==x){splay(now);return k+1;}
k+=sum[now];
now=ch[now][1];
}
}
}
inline int find_kth(int x){
int now=rt;
while(1){
if(ch[now][0]&&x<=size[ch[now][0]])
now=ch[now][0];
else{
int temp=(ch[now][0]?size[ch[now][0]]:0)+sum[now];
if(x<=temp) return val[now];
x-=temp;
now=ch[now][1];
}
}
}
inline int pre(){
int now=ch[rt][0];
while(ch[now][1]) now=ch[now][1];
return now;
}
inline int next(){
int now=ch[rt][1];
while(ch[now][0]) now=ch[now][0];
return now;
}
inline void del(ci x){
find(x);
if(sum[rt]>1){sum[rt]--;update(rt);return ;}
if(!ch[rt][0]&&!ch[rt][1]){clear(rt);rt=0;return ;}
if(!ch[rt][0]){
int old_root=rt;
rt=ch[rt][1];
f[rt]=0;
clear(old_root);
return ;
}
if(!ch[rt][1]){
int old_root=rt;
rt=ch[rt][0];
f[rt]=0;
clear(old_root);
return ;
}
int prev=pre(),old_root=rt;
splay(prev);
ch[rt][1]=ch[old_root][1];
f[ch[old_root][1]]=rt;
clear(old_root);
update(rt);
}
int main(){
scanf("%d",&n);
while(n--){
int opr,x;
scanf("%d%d",&opr,&x);
if(opr==1) insert(x);
if(opr==2) del(x);
if(opr==3) printf("%d\n",find(x));
if(opr==4) printf("%d\n",find_kth(x));
if(opr==5){insert(x);printf("%d\n",val[pre()]);del(x);}
if(opr==6){insert(x);printf("%d\n",val[next()]);del(x);}
}return 0;
}tarjan dalao救世界!
其实本体是好写的模拟...
标签:建议 splay 思考 ios 设立 大数 旋转 世界 变量
原文地址:https://www.cnblogs.com/648-233/p/12163776.html