标签:快速幂 算法 等于 问题 状压dp 填充 递推 mamicode 部分
也是基于状压dp的一种。最经典的问题莫过于棋盘覆盖了,例如用1*2orL型骨牌覆盖N*M棋盘得方案个数。一般M不会太大。

例如这一道,由于形状特殊,轮廓线长度为M+1才可,递推时只要满足轮廓线前面的格子都是满的且当前放置方案合法即可。
有四种不同放置方法,
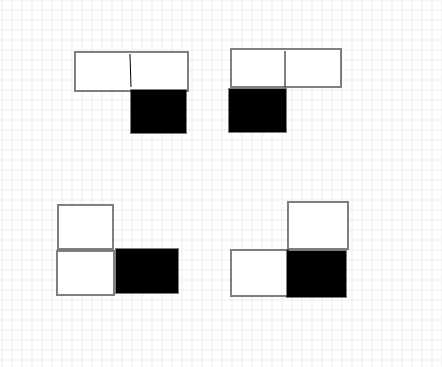
黑色部分为当前枚举的位置(i,j),相当于固定好放置方法。然后递推就好了。
相比较而言,矩阵快速幂得做法效率更好,我们观察行与行得转移关系会发现相邻两行的状态转移关系和具体的行数无关,转移N次等价于关系矩阵a得N次方,而矩阵乘法又可以加速从而优化算法。
对于a[S1][S2]只要初始上一行状态为S1,下一行默认为0,经过一些填充操作之后S1=all,下一行->S2 就说明S1->S2是可行的转移方式。
还要注意为了便于理解,把f(0,S)表示第0行状态为S得方案个数,显然有f(0,all)=1 f(0,other)=0。相等于默认第0行已经铺满,
标签:快速幂 算法 等于 问题 状压dp 填充 递推 mamicode 部分
原文地址:https://www.cnblogs.com/zzqc/p/12173057.html