周期信号的傅里叶级数

标签：矩形   理论   部分   span   length   信号处理   不同   傅里叶级数   soft   

**探讨问题：**
对一个周期波形为ft=1，0<t<T/2;ft=-1,T/2<t<T进行傅里叶展开，取不同级数对波形的影响
一、理论推导部分：由于不方便插入公式，因此省去推导部分；
二、代码部分：
```
N=3;%展开式的项数为2N+1项

T=1;
fs=1/T;
N_sample=128;%每个周期的采样点数
dt=T/N_sample;

t=0:dt:10*T-dt;
n=-N:N;
Fn=sinc(n/2).*exp(-j*n*pi/2);

F(N+1)=0;
ft=zeros(1,length(t));

for m=-N:N
ft=ft+Fn(m+N+1)*exp(j*2*pi*m*fs*t);

end

plot(t,ft);
```
所得波形图：
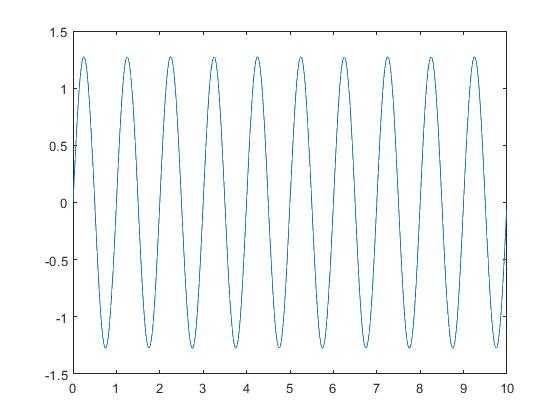
（1）N=1

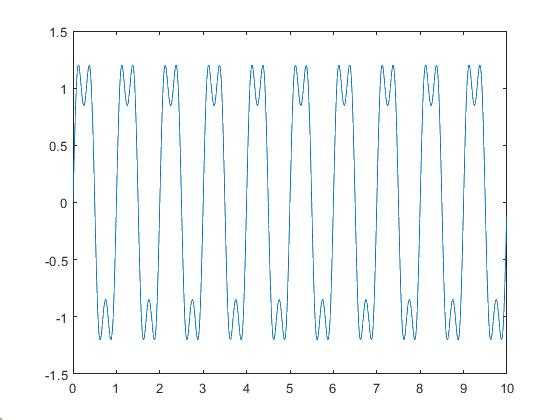
（2）N=3

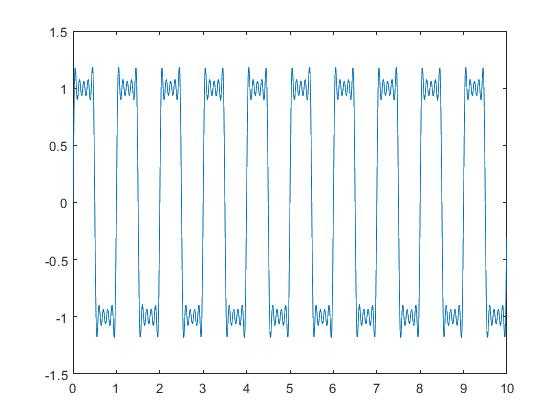
（3）N=10

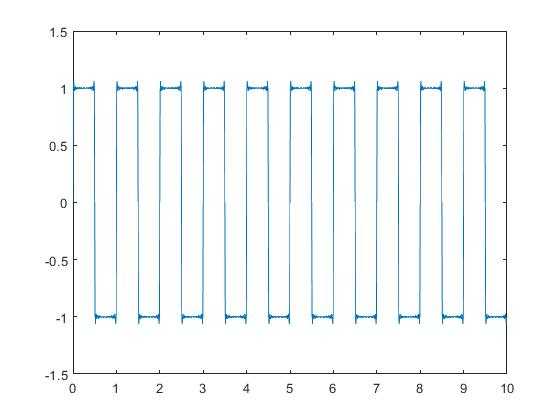
（4）N=100

三、分析部分：
　　从以上几个图得知，随着N的值不断增大，我们得到的波形越来越趋近于原始波形的形状，同时也出现了不同数目的小尖峰；小尖峰的存在，是由于矩形波对应的频域是（sinx）/x，无限长；具体分析过程可翻看数字信号处理教材吉伯斯（Gibbs）现象。

周期信号的傅里叶级数

标签：矩形   理论   部分   span   length   信号处理   不同   傅里叶级数   soft   

原文地址：https://www.cnblogs.com/qw-blog/p/hunnu-qw.html