标签:dde ros 通过 讲解 cos 红色 部分 坐标 and
傅里叶变换是一个很重要的变换方法。大部分人对傅里叶变换的理解就是,它实现了信号从时域到频域的转换,而从数学的角度来看,傅里叶变换其实就是一种基底变换(通俗地说就是改变原来的坐标系)。然而,不论从什么角度来理解傅里叶变换,我们只要记住,它的本质就是一个序列\(f\)到另一个序列的\(F\)转换(连续或离散)。
傅里叶变换的研究和应用都非常多,因此本文不再赘述相关的内容,如果想通俗且深入地理解傅里叶变换,我推荐马同学的博客。
一般的傅里叶变换通常指以下的公式:
\[F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\]
为了和离散傅里叶变换区别,我们称其为连续傅里叶变换。
由前文可知,连续傅里叶变换的公式如下:
\[F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\]
现实中,我们一般无法得到连续的观察序列\(f(t)\),只能通过采样的方式得到离散的子序列\(f[k]\)。比较严谨的定义是:从连续的时间序列\(f(t)\)中按给定周期\(T\)采样\(N\)个点,\(f[0],f[1],\dots,f[N-1]\),这\(N\)个点组成了\(f(t)\)的一个离散子序列\(f[k]\)。
我们用离散序列\(f[k]\)来估计\(f(t)\)的傅里叶变换结果\(F(j\omega)\),基于dft的公式,很容易可以得到:
\[\begin{aligned}
F(j\omega)&=\int_{0}^{(N-1)T}f(t)e^{-j\omega t}dt\&=f[0]e^{-j0}+f[1]e^{-j\omega T}+\dots+f[k]e^{-j\omega kT}+\dots+f[N-1]e^{-j\omega(N-1)T}\&=\sum_{k=0}^{N-1}f[k]e^{-j\omega kT}
\end{aligned}\]
因此,我们得到了基于离散子序列\(f[k]\)的变换公式:
\[F(j\omega)=\sum_{k=0}^{N-1}f[k]e^{-j\omega kT}\]
实际上,我们也无法得到真正的\(F(j\omega)\)(连续的),只能用插值的方式做估计(离散的),类似于从\(f(t)\)中采样得到\(f[k]\),我们也可以取\(F(j\omega)\)的\(N\)个离散值来做估计。由于\(f[k]\)是以\(T\)为周期采样的,所以\(\omega\)的插值范围应该落在区间\([0, \frac{2\pi}{T})上\)(假设有\(\frac{2\pi}{T_{1}}>\frac{2\pi}{T}\),则\(T_{1}< T\),比我们采样的周期小)。在区间\([0, \frac{2\pi}{T})\)中均匀取\(N\)个点,可以得到\(\omega\)的\(N\)个插值点:
\[\omega=0,\frac{2\pi}{NT},\frac{2\pi}{NT}\times 2,\dots,\frac{2\pi}{NT}\times n,\dots,\frac{2\pi}{NT}\times(N-1)\]
把\(\omega\)代入上面的公式,可以得到离散傅里叶变换(dft)公式:
\[F[n]=\sum_{k=0}^{N-1}f[k]e^{-j\frac{2\pi}{N}nk},(n=0,1,\dots,N-1)\]
我们将离散傅里叶变换简称为dft,为了方便起见,后面统一用dft表示离散傅里叶变换。
根据上面的公式,可以很容易计算出任何离散序列的dft,对应的代码(python)如下:
import cmath
import numpy as np
def dft(ts):
""" discrete fourier transformer
"""
N = len(ts)
F = np.zeros(N, dtype=np.complex)
for n in range(N):
for k, f in enumerate(ts):
F[n] += f * cmath.exp(-2j*cmath.pi/N*(n*k))
return F从代码中可以看到,计算dft需要做嵌套的\(N\)次遍历,因此使用这种方式计算dft的时间复杂度是\(O(n^{2})\),当\(n\)值很大时(比如\(n=1000\)),dft的计算会相当耗时,所以现实中一般使用快速傅里叶变换(fft)来计算dft。
快速傅里叶变换(fft)是一种优化的dft计算方法,核心思想是分治,为了方便,后面统一用fft指代快速傅里叶变换算法。在讲解fft之前,先复习一下dft的公式,
\[F[n]=\sum_{k=0}^{N-1}f[k]e^{-j\frac{2\pi}{N}nk},(n=0,1,\dots,N-1)\]
公式中的变量\(e^{-j\frac{2\pi}{N}nk}\)看起来有些复杂,我们可以用简单的变量来代替,所以令
\[W_{N}^{nk}=e^{-j\frac{2\pi}{N}nk}\]
则原dft公式可以重写成:
\[F[n]=\sum_{k=0}^{N-1}f[k]W_{N}^{nk},(n=0,1,\dots,N-1)\]
变量\(W_{N}^{nk}\)有以下几个性质:
这几个性质的证明都很简单,对于性质1,我们有
\[W_{N}^{mN}=e^{-j\frac{2\pi}{N}mN}=e^{-j2m\pi}=1\]
对于性质2,我们有
\[W_{N}^{mN+N/2}=W_{N}^{N/2}=e^{-j\frac{2\pi}{N}\frac{N}{2}}=e^{-j\pi}=-1\]
对于性质3,我们有
\[W_{N}^{d+mN}=W_{N}^{mN}W_{N}^{d}=W_{N}^{d}\]
对于性质4,我们有
\[W_{N}^{d+mN+N/2}=W_{N}^{d}W_{N}^{mN}W_{N}^{N/2}=-W_{N}^{d}\]
这几个性质正是后面我们推导fft时所要用到的。
假设\(N\)是2的幂,即\(N=2^{l}, l=1,2,3,\dots\)。我们对\(\sum_{k=0}^{N-1}f[k]W_{N}^{nk}\)中的项按\(k\)的奇偶分组,可以得到:
\[\begin{aligned}
F[n]&=\sum_{k=0}^{N-1}f[k]W_{N}^{nk},(n=0,1,\dots,N-1)\&=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N}^{2nk}+W_{N}^{n}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N}^{2nk}\&=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{nk}+W_{N}^{n}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{nk}
\end{aligned}\]
当\(n\geq\frac{N}{2}\)时,不妨令\(n=n_{1}+\frac{N}{2}, n_{1}=0,1,2,\dots,\frac{N}{2}-1\),则有:
\[\begin{aligned}
F[n]&=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{nk}+W_{N}^{n}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{nk}\&=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{n_{1}k+kN/2}+W_{N}^{n_{1}+N/2}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{n_{1}k+kN/2}\&=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{n_{1}k}-W_{N}^{n_{1}}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{n_{1}k}
\end{aligned}\]
进一步地,我们令
\[G[n]=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{nk}, H[n]=\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{nk}\]
故当\(0\leq n<\frac{N}{2}\)时,有:
\[F[n]=G[n]+W_{N}^{n}H[n],F[n+N/2]=G[n]-W_{N}^{n}H[n]\]
举例来说,当\(N=8\)时,有
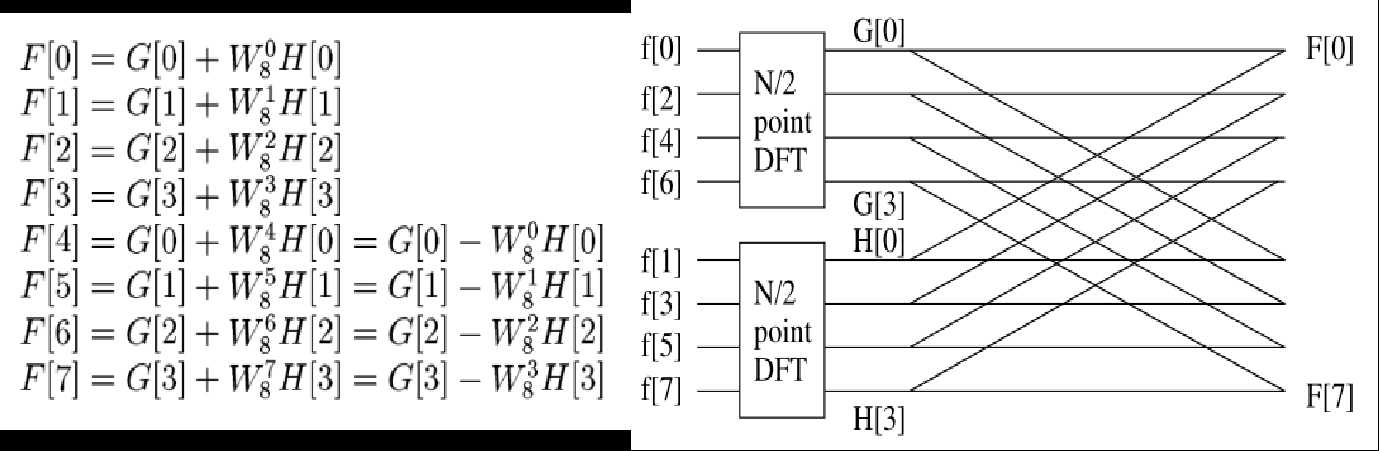
因为\(N\)是2的幂,所以\(G[n]\)和\(H[n]\)还可以像这样用奇偶分组的方式进一步拆解为更小粒度的分组

上述所有图里小方框内的数字表示的是原序列下标\(n\),划分到最小粒度时,有\(N=2\),即
\[G[n]=f(n), H[n]=f(n)\]

此时,\(G[n]\)项中的\(f[2k]W_{N/2}^{nk}\)里,\(k=0\);\(H[n]\)项中的\(f[2k+1]W_{N/2}^{nk}\)里,\(k=0\)。
通过“蝴蝶变换”(buttferfly transform),我们可以依次从“小粒度的分组”不断合并得到“大粒度的分组”,下图中的四条红色线段和对应的点应组成了一个蝴蝶变换。

更具体的蝴蝶变换如下图所示:

观察每次分组中\(k\)值的变化,可以发现每次分组是按二进制位最后一位来判断的(0为偶,1为奇)

因此,我们在做分组的时候,可以使用递归的方式来做,每次递归时按二进制位的最后一位对序列分组,具体代码(python)如下:
import cmath
import numpy as np
def wnk(N, n):
""" get W_N^n
"""
return cmath.exp(-2j*n*cmath.pi/N)
def recursive_fft(f):
""" recursive of fast fourier transform
"""
N = len(f) # N is power of 2
if N < 2:
return f
F = np.zeros(N, dtype=np.complex)
G = recursive_fft([x for i,x in enumerate(f) if i%2 == 0]) # even
H = recursive_fft([x for i,x in enumerate(f) if i%2 == 1]) # odd
for i, (g, h) in enumerate(zip(G, H)):
# butterfly transform
F[i] = g + wnk(N, i)*h
F[i+N//2] = g - wnk(N, i)*h
return F使用递归的方法计算fft需要用到额外的变量G和H,而且递归有深度的限制,最好不使用递归便能达到我们迭代更新的目的。回顾我们之前的思路,是按“大粒度的分组”->“小粒度的分组”来进行更新的,如果能反过来,按“小粒度的分组”->“大粒度的分组”来更新,那么就不需要递归了。问题在于如何得到“小粒度的分组”?既然我们每次是根据\(k\)的最后一个二进制位来决定分组,那么如果我们将\(k\)的二制位倒置的话,不就可以得到按顺序排列的“小粒度分组”吗

所以非递归的fft思路就很清晰了,
非递归fft的代码(python)如下所示:
import cmath
import numpy as np
def wnk(N, n):
""" get W_N^n
"""
return cmath.exp(-2j*n*cmath.pi/N)
def get_bit(n):
""" get highest bit of n
"""
bit = 0
while n != 0:
n >>= 1
bit += 1
return bit
def flip_bits(bits, n):
""" flip n bit of bits
"""
assert n >= 0
if n == 0:
return bits
y = 0
while n > 0:
y <<= 1
y |= bits&1
bits >>= 1
n -= 1
return y
def fft(f):
""" fast discrete fourier transformer
"""
N = len(f) # N is power of 2
l = get_bit(N)
# re-arange f by flipping bits
F = np.zeros(N, dtype=np.complex)
for i, a in enumerate(f):
F[flip_bits(i, l-1)] = a
step = 1
while step < N:
for i in range(0, N, 2*step):
for j in range(i, i+step):
# butterfly transform
a = F[j] + wnk(2*step, j)*F[j+step]
b = F[j] - wnk(2*step, j)*F[j+step]
F[j] = a
F[j+step] = b
step *= 2
return F到这里,fft的计算逻辑已经基本最优了,但是,注意到每次分组内做蝴蝶变换时需要计算\(W_{N}^{n}\),而实际上每次按序遍历\(G\)和\(H\)时,\(W_{N}^{n}\)是按\(W_{N}^{1}\)等比递增的,所以这里可以进一步优化来减少计算量。代码(python)如下所示:
import cmath
import numpy as np
WNK = [cmath.exp(-2j*cmath.pi/(1<<n)) for n in range(64)]
def get_bit(n):
""" get highest bit of n
"""
bit = 0
while n != 0:
n >>= 1
bit += 1
return bit
def flip_bits(bits, n):
""" flip n bit of bits
"""
assert n >= 0
if n == 0:
return bits
y = 0
while n > 0:
y <<= 1
y |= bits&1
bits >>= 1
n -= 1
return y
def fft(f):
""" fast discrete fourier transformer
"""
N = len(f)
l = get_bit(N)
# re-arange ts by flipping bits
F = np.zeros(N, dtype=np.complex)
for i, a in enumerate(f):
F[flip_bits(i, l-1)] = a
step = 1
cnt = 1
while step < N:
for i in range(0, N, 2*step):
w = 1.0
for j in range(i, i+step):
# butterfly transform
a = F[j] + w*F[j+step]
b = F[j] - w*F[j+step]
w *= WNK[cnt]
F[j] = a
F[j+step] = b
step *= 2
cnt += 1
return F至此,fft的完整过程基本讲解完毕。
傅里叶逆变换(idft)的公式如下:
\[f[n]=\frac{1}{N}\sum_{k=0}^{N-1}F[k]e^{j\frac{2\pi}{N}nk},(n=0,1,\dots,N-1)\]
对比dft的公式可以发现二者基本一致,只不过\(W_{N}^{nk}=e^{j\frac{2\pi}{N}nk}\),同时多了一个因子\(\frac{1}{N}\)。所以,只要在fft的过程中替换\(W_{N}^{nk}\),并把最后的结果除以\(N\)就可以得到ifft。
最后,完整的fft和ifft代码(python)如下所示:
import cmath
import numpy as np
WNK = [cmath.exp(-2j*cmath.pi/(1<<n)) for n in range(64)]
def check_power2(n):
""" check `n` is or not power of 2
"""
return n > 0 and n&(n-1) == 0
def get_bit(n):
""" get highest bit of n
"""
bit = 0
while n != 0:
n >>= 1
bit += 1
return bit
def flip_bits(bits, n):
""" flip n bit of bits
"""
assert n >= 0
if n == 0:
return bits
y = 0
while n > 0:
y <<= 1
y |= bits&1
bits >>= 1
n -= 1
return y
def fft(ts):
""" fast fourier transformer
"""
return fdft(ts)
def ifft(ts):
""" reverse fast fourier transformer
"""
return fdft(ts, reverse=True)
def fdft(f, reverse=False):
""" fast discrete fourier transformer
"""
N = len(f)
if not check_power2(N):
raise ValueError("f length is not power of 2")
l = get_bit(N)
# re-arange ts by flipping bits
F = np.zeros(N, dtype=np.complex)
for i, a in enumerate(f):
F[flip_bits(i, l-1)] = a
factor = lambda x, a: x*a
if reverse:
factor = lambda x, a: x/a
step = 1
cnt = 1
while step < n:
for i in range(0, N, 2*step):
w = 1.0
for j in range(i, i+step):
# butterfly transform
a = F[j] + w*F[j+step]
b = F[j] - w*F[j+step]
w = factor(w, WNK[cnt])
F[j] = a
F[j+step] = b
step *= 2
cnt += 1
return F/N if reverse else F使用fft可以加速多项式乘法。首先,\(n\)次多项式\(f(x)\)的定义如下,
\[f(x)=a_{0}+a_{1}x^{1}+a_{2}x*{2}+\dots+a_{n}x^{n}\]
类似地,有\(n\)次多项式\(g(x)\),
\[g(x)=b_{0}+b_{1}x^{1}+b_{2}x*{2}+\dots+b_{n}x^{n}\]
一般情况下,我们使用嵌套遍历来计算\(f(x)g(x)\),代码(python)如下
def poly(ar, br):
""" defatul polynomial multiplication: n*n
"""
n = len(ar)
cr = np.zeros(2*n-1)
for i, a in enumerate(ar):
for j, b in enumerate(br):
cr[i+j] += a*b
return cr\(f(x)g(x)\)的时间复杂度是\(O(n^{2})\),使用傅里叶变换可以优化\(f(x)g(x)\)(复杂度降至\(O(n\log{n})\))。思路是:
则\(h(x)=f(x)g(x)\),上式过程在理论上应该是成立的(具体数学证明请另外搜索相关资料),具体的代码(python)如下:
def poly_fft(ar, br):
""" polynomial multiplication by fft: nlogn
"""
n = len(ar) # assume ar.length == br.length and ar.length is power of 2
padded = np.zeros(n) # pad to 2n
far = fft(np.append(ar, padded))
fbr = fft(np.append(br, padded))
fcr = far * fbr
cr = np.array([x.real for x in ifft(fcr)])
return cr[:-1]fft和ifft的时间复杂度是\(O(n\log{n})\),我们用fft做多项式乘法时,做了3次变换,一次向量乘法,因此时间复杂度为\(O(n\log{n})\)。可以用简单的实验对比一下两种方法的效率(fft和ifft是我们之前实现的),代码(python)如下
import cmath
import functools
import time
import numpy as np
def timer(func):
@functools.wraps(func)
def func_with_timer(*args, **kwargs):
start = time.time()
res = func(*args, **kwargs)
end = time.time()
print(f"{func.__name__} cost {end - start} seconds")
return res
return func_with_timer
@timer
def poly_fft(ar, br):
""" polynomial multiplication by fft: nlogn
"""
n = len(ar) # assume ar.length == br.length and ar.length is power of 2
padded = np.zeros(n) # pad to 2n
far = fft(np.append(ar, padded))
fbr = fft(np.append(br, padded))
fcr = far * fbr
cr = np.array([x.real for x in ifft(fcr)])
return cr[:-1]
@timer
def poly(ar, br):
""" defatul polynomial multiplication: n*n
"""
n = len(ar)
cr = np.zeros(2*n-1)
for i, a in enumerate(ar):
for j, b in enumerate(br):
cr[i+j] += a*b
return cr
if __name__ == '__main__':
n = 1024
f = np.ones(n)
g = np.ones(n) * 2.0
p = poly(f, g)
fp = poly_fft(f, g)
for i in range(int(n*0.1)):
print(p[i], fp[i]) 取\(n=1024\)时,对比结果如下:
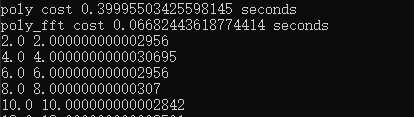
从结果上看,使用fft的确要效率更高,而且二者的计算结果基本一样。
对fft的介绍就到这里为止了,由于本人对傅里叶变换的了解不多,应用也比较少,所以只能从算法角度来谈谈个人对fft的认识,并总结一些可能比较重要的细节,希望能够为读者提供帮助和参考价值。另外,本文的公式和代码比较多,存在错误,烦请指出,谢谢!
标签:dde ros 通过 讲解 cos 红色 部分 坐标 and
原文地址:https://www.cnblogs.com/nkuhyx/p/12170152.html