标签:user 方法 比较 操作 cpp ref 假设 code lock
这是一种本题对所有树都适用的树分块做法。
___
树分块的瓶颈在于,当树为菊花图时,访问的联通块比较多。本质上说,单次询问访问了许多边,个数为\(O(n)\)。
所以想办法使得不再访问那么多边。
我们对原树进行分块,一定要保证是块内连通,设块的大小为\(O(S)\)。
我们再建一棵树,这棵树是原树边集为原边集去掉连接块与块之间的边,剩下的边。也就是说,原树形成了森林,每一棵树就是一个块。
我们定义连接块与块之间的边称为虚边,块内的边称为实边。以1为根后,原树就有了父子关系。定义如果一个点的儿子与其之间的边为虚边,那么这个儿子叫虚儿子,否则叫实儿子。就像这样。
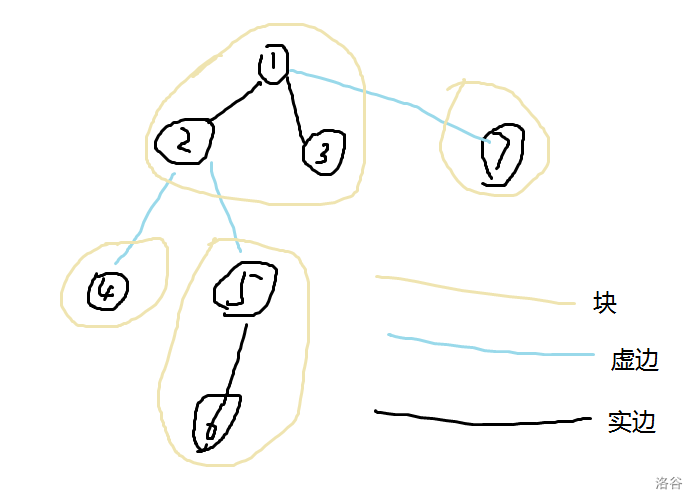
接下来,我们在每个点\(x\)都挂一个可重集合\(Set(x)\)。集合内保存的是该点所有虚子树中所有节点的权值。
我们定义\(fa[x]\)表示x的原树的父亲节点,\(top[x]\)表示x所在块内的深度最小的点(显然唯一)。\(size[x]\)表示编号为x的节点所在块的节点数量。我们接下来要频繁用到它们。
至于分块的方式,我使用的是bfs分块(证明处介绍),尚不明确是否所有块内联通式分块均能保证复杂度。
至此,数据结构部分完结,下面开始讲具体要如何操作。
注:块的大小为S,读入u,x。
如果\(fa[u]\)的块的大小\(size[fa[u]]\leq S-1\),那么我们将u并入\(fa[u]\)所在的块.如果\(fa[u]\)的块的大小\(size[fa[u]]= S\),那么我们将u单独分一块.这很显然,就是普通树分块的方法.
得到新节点的块归属之后,接下来是这段操作,也是最为关键的操作,请读者仔细理解。
int data=value[u];
while (true) {
u=fa[top[u]];
if (u) set[u].insert(data);
else break;
}它表示的意思是,对于u,其到根路径上会经过一些块的内部。对于每一个经过的块,我们将它在这条路径上深度最深的节点所在的可重集合中插入u的权值。
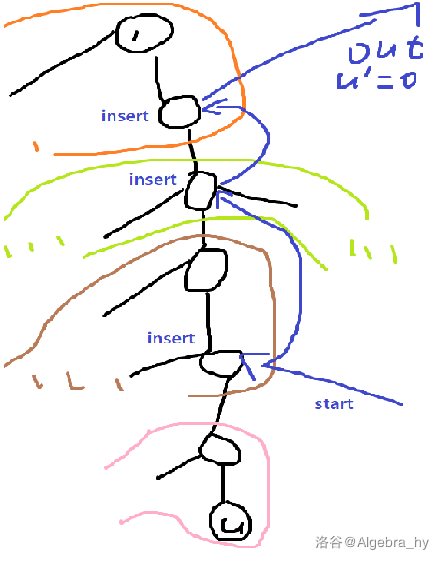
有什么作用呢?即将呈现。
我们遍历u所在的块内且在u子树内的点。对于遍历到的每一个点v,我们在v的可重集合内(也就是一颗平衡树中)查到权值大于x的节点个数,再根据v自身的权值是否大于x决定答案要不要再加上1。对于遍历到的每一个点利用上句方法算出的答案求和即为操作(0,u,x)的答案。
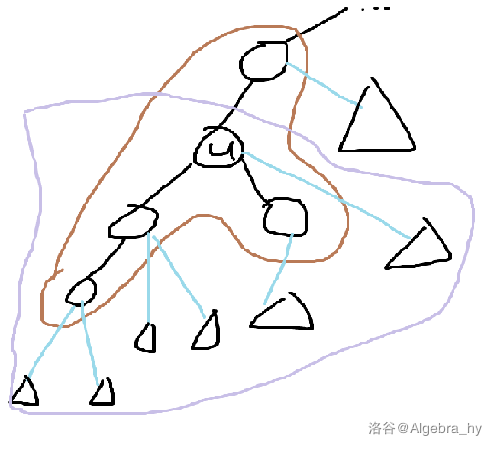
我们先前定义过:
我们在每个点\(x\)都挂一个可重集合\(Set(x)\)。集合内保存的是该点所有虚子树中所有节点的权值。
是不是一目了然了?我们不再需要去扫描每一个节点的虚子树,而是在原树基础上新建的“块森林”中的那棵块树上dfs统计答案。
联想刚才的操作2,这里会变得十分简单。
//操作(1,u,x)
int data=value[u];
while (true) {
u=fa[top[u]];
if (u) set[u].delete(data),set[u].insert(x);
else break;
}做完了。
设块的大小为\(S\)且始终为定值,节点总数\(n\)可能随着操作而变化,但是定格在每个时刻\(n\)肯定是不变的。
我自己口胡的方法和名字,未上网考证是否已出现过。
具体是这样做:我们先从一棵树的根开始bfs,选前\(S\)个点,然后将它们删掉,这棵树树裂变成森林。再对森林从每一颗树的根重复以上操作。
根据刚才的分块方式,假设虚边上端父亲节点所在块的大小小于\(S\),那么这条虚边下端儿子节点定然会在初始分块时或操作进行时分给其父亲所在的块,故这条边是实边,与假设不符。
这也许是一个重要性质。具体地说,虽然无法保证块的总数为\(O(\frac{n}{S})\),但是可以保证任意一个节点到根的路径上仅仅会经过最多\(\left\lceil\dfrac{n}{S}\right\rceil\)个块,其中当前节点\(x\)所在的块大小为\(0\lt size[x] \leq S\),其余的块的大小为\(S\)。
证明如下:假设对于一个点,其到根路径上存在块的数量\(M\geq \left\lceil\dfrac{n}{S}\right\rceil+1\),则存在虚边条数至少为\(\left\lceil\dfrac{n}{S}\right\rceil\)。根据引理1,至少存在\(\left\lceil\dfrac{n}{S}\right\rceil\)个大小为S的块。去掉这\(\left\lceil\dfrac{n}{S}\right\rceil\)个大小为S的块,剩余块数\(M - \left\lceil\dfrac{n}{S}\right\rceil \geq 1\),则剩余的节点总数\(X\gt 0\)。则此时至少存在\(\left\lceil\dfrac{n}{S}\right\rceil\times S+X \geq n+X \gt n\)个节点。而此时节点数量先前被设为\(n\),故假设不成立。再根据代码,循环次数为\(M-1\leq\left\lceil\dfrac{n}{S}\right\rceil-1 \leq \left\lfloor\dfrac{n}{S}\right\rfloor\),所以即定理1成立。
证明:首先是时间复杂度。根据定理1,每个节点的权值会被插入\(O(\dfrac{N}{S})\)次,插入及查询区间内权值个数可用平衡树实现。单次询问时间复杂度为\(O(\dfrac{N}{S}logN)\)。
然后是空间复杂度。由于插入\(O(\dfrac{N}{S})\)次,平衡树空间复杂度为\(O(N)\),故空间复杂度\(O(\dfrac{N^2}{S})\)。
当取\(S=\sqrt{N}\)时,定理2成立。
___
总结
《Gty的妹子树》中,普通的树分块算法已经基本被宣告完蛋。但是我们如果尝试优化其短处,并尝试继续抢救,也许会发现许多新的道理与思路。
新人第一次写证明,有问题还请大家指出。特别鸣谢双管荧光灯WCAu巨佬提供定理1的证明思路的方向。希望有大佬能够给出任意的块内联通式树分块能否保证复杂度的判断和证明。
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <queue>
using namespace std;
const int S=60003,M=7500000;
int n,m,a[S],bl[S],top[S],fa[S],nn,cnt=0,s[S],lasans=0;
int rt[S],ch[M][2],sz[M],rnd[M],data[M],tot=0;
queue<int> q,q2;
struct Graph
{
int h[S],nx[S<<1],v[S<<1],eg;
inline void init(){memset(h,0,sizeof(h));eg=1;}
Graph(){init();}
inline void egadd(int uu,int vv)
{
nx[++eg]=h[uu];h[uu]=eg;
v[eg]=vv;
}
}g,rg;
void split(int now,int k,int &x,int &y)
{
if (!now) x=y=0;
else
{
if (data[now]<=k)
{
x=now;
split(ch[now][1],k,ch[x][1],y);
}
else
{
y=now;
split(ch[now][0],k,x,ch[y][0]);
}
sz[now]=sz[ch[now][0]]+sz[ch[now][1]]+1;
}
}
int merge(int x,int y)
{
if (!x || !y) return x+y;
else
if (rnd[x]<rnd[y])
{
ch[x][1]=merge(ch[x][1],y);
sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1;
return x;
}
else
{
ch[y][0]=merge(x,ch[y][0]);
sz[y]=sz[ch[y][0]]+sz[ch[y][1]]+1;
return y;
}
}
inline int nnd(int x)
{
++tot;
rnd[tot]=rand();
data[tot]=x;
sz[tot]=1;
return tot;
}
inline void insert(int &root,int x)
{
int ta,tb;
split(root,x,ta,tb);
root=merge(merge(ta,nnd(x)),tb);
}
inline void del(int &root,int x)
{
int ta,tb,tc;
split(root,x-1,ta,tb);
split(tb,x,tb,tc);
tb=merge(ch[tb][0],ch[tb][1]);
root=merge(merge(ta,tb),tc);
}
inline int cal(int &root,int x)
{
int ta,tb;
split(root,x,ta,tb);
int ret=sz[tb];
root=merge(ta,tb);
return ret;
}
void dfs_1(int x)
{
for (int i=g.h[x];i;i=g.nx[i])
if (g.v[i]!=fa[x])
{
fa[g.v[i]]=x;
dfs_1(g.v[i]);
}
}
void get_block()
{
q.push(1);
while (!q.empty())
{
int y=q.front();q.pop();
++cnt;
q2.push(y);
for (int o=1;o<=nn;++o)
{
if (q2.empty()) break;
int x=q2.front();q2.pop();
bl[x]=cnt;top[x]=y;++s[bl[x]];
for (int i=g.h[x];i;i=g.nx[i])
if (g.v[i]!=fa[x])
q2.push(g.v[i]);
}
while (!q2.empty()) {q.push(q2.front());q2.pop();}
}
}
int dfs_2(int x,int y)
{
int ret=cal(rt[x],y)+(a[x]>y);
for (int i=rg.h[x];i;i=rg.nx[i])
ret+=dfs_2(rg.v[i],y);
return ret;
}
int main()
{
srand(23112);
scanf("%d",&n);
for (int i=1;i<n;++i)
{
int uu,vv;
scanf("%d%d",&uu,&vv);
g.egadd(uu,vv);g.egadd(vv,uu);
}
for (int i=1;i<=n;++i)
scanf("%d",a+i);
scanf("%d",&m);
nn=sqrt(n+m-1)+1;
dfs_1(1);
get_block();
for (int i=1;i<=n;++i)
{
int j=i;
while (j)
{
j=fa[top[j]];
if (j) insert(rt[j],a[i]);
}
if (bl[i]==bl[fa[i]])
rg.egadd(fa[i],i);
}
int op,x,y;
while (m--)
{
scanf("%d%d%d",&op,&x,&y);
x^=lasans;y^=lasans;
if (op==0)
printf("%d\n",lasans=dfs_2(x,y));
else if (op==1)
{
int o=x;
while (o)
{
o=fa[top[o]];
if (o)
{
del(rt[o],a[x]);
insert(rt[o],y);
}
}
a[x]=y;
}
else
{
fa[++n]=x;
a[n]=y;
if (s[bl[x]]<nn)
{
bl[n]=bl[x];
++s[bl[x]];
top[n]=top[x];
rg.egadd(x,n);
}
else
{
bl[n]=++cnt;
s[cnt]=1;
top[n]=n;
}
int o=n;
while (o)
{
o=fa[top[o]];
if (o) insert(rt[o],y);
}
}
}
return 0;
}标签:user 方法 比较 操作 cpp ref 假设 code lock
原文地址:https://www.cnblogs.com/Algebra-hy/p/12177281.html