标签:方向 转换 tps size 作用 表达 target 元素 内容
1、系数矩阵
前面学习了矩阵很多基础知识,那么遇到具体的线性方程组该怎么办呢?该怎么转换为矩阵来求解呢?如下图所示,A为系数矩阵,X是未知数矩阵,B是常数矩阵。
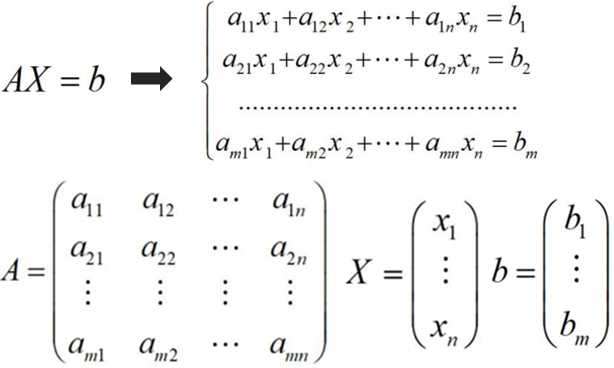
2、矩阵转置
简单来说就是矩阵的行元素和列元素互相调换一下。
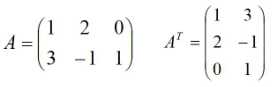
下面列出一些矩阵转置常用的公式
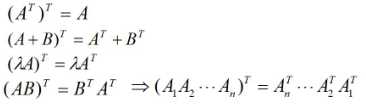
这些都没有什么好说的,都比较好理解,要注意的是就是最后一个公式的前后的顺序是不同的。
3、对称矩阵
如果满足$A^{T}=A$,那么A就是对称矩阵
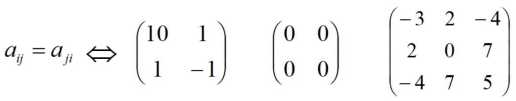
4、逆矩阵
A为n阶方阵,如果说存在n阶方阵B,使得AB=BA=I(I为单位矩阵),那么就称A、B互为逆矩阵,记作:B=A-1
性质(前提矩阵可逆):
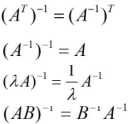
矩阵的秩很重要,对后面特征值,特征向量的理解很重要,要重点注意这个地方。
对于一个$S\times N$的矩阵:$A=\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ a_{s1} & a_{s2} & \cdots & a_{sn}\end{bmatrix}$
矩阵A的每一行可以看作一个N维向量:$\alpha _{i}=(a_{i1},a_{i2},\cdots ,a_{in}),i=1,2,\cdots ,s$,所以$\alpha _{1},\alpha _{2},\cdots ,\alpha _{s}$称作A的行向量
矩阵A的每一列也可以看作一个S维向量:$\beta _{j}=\begin{bmatrix}a_{1j}\\ a_{2j}\\ \vdots \\ a_{ij}\end{bmatrix},j=1,2,\cdots ,n$,所以$\beta _{1},\beta _{2},\cdots ,\beta _{n}$称作A的列向量。
那么矩阵的秩到底表示什么呢?
比如说有一个矩阵$A=\begin{bmatrix}1 & 1 & 3 &1 \\ 0 & 2&-1 & 4\\ 0 & 0 & 0 & 5\\ 0 & 0 & 0 & 0\end{bmatrix}$
矩阵A的行向量组为:$\begin{matrix}\alpha _{1}=(1,1,3,1) &\alpha _{2}=(0,2,-1,4) \\ \alpha _{3}=(0,0,0,5) & \alpha_{4}=(0,0,0,0)\end{matrix}$
现在我们需要求这个行向量组的极大线性无关组,假设有$k_{1}\alpha _{1}+k_{2}\alpha _{2}+k_{3}\alpha _{3}=0$。具体代入如下图所示
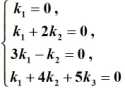
解得$k_{1}=k_{2}=k_{3}=0$,即$\alpha _{1},\alpha _{2},\alpha _{3}$线性无关。
由于矩阵里面含有一个零向量,所以这个零向量必然和矩阵里面其他向量线性相关,所以向量组:$\alpha _{1},\alpha _{2},\alpha _{3},\alpha _{4}$的秩为3。简单来说,矩阵的秩就是矩阵里面的所有向量最大的线性无关的数目。
对于列向量同理可得:$\beta _{3}=\frac{7}{2}\beta _{1}-\frac{1}{2}\beta _{2}+0\beta _{4}$,但$\beta _{1},\beta _{2},\beta _{4}$线性无关,所以向量组:$\beta _{1},\beta _{2},\beta _{3},\beta _{4}$的秩为3,综上所述,即矩阵的行秩等于列秩。
那么矩阵的秩到底该怎么来理解呢?以下内容参考了知乎大神的理解:https://www.zhihu.com/question/21605094
可以对二维图形(实际上就是代表一个矩阵)进行旋转,比如用旋转矩阵:$\begin{bmatrix}\cos(\theta ) &-\sin (\theta ) \\ \sin (\theta ) & \cos(\theta )\end{bmatrix}$去乘以二维图形代表的矩阵。
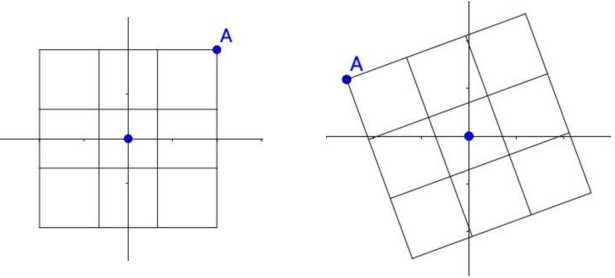
变换后依然是二维的,所以旋转矩阵的秩为2
在假如说通过这样的矩阵$\begin{bmatrix}1 & -1\\ 1 & -1\end{bmatrix}$来对图形进行旋转。
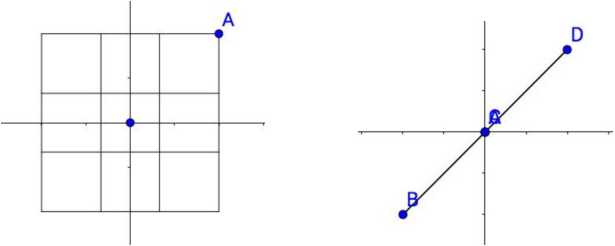
变换后是一维的,所以这个旋转矩阵的秩为1
矩阵中最大不相关向量的个数就是秩了。
举个例子就很容易理解,大家排队买票。如果大家互相不认识,那就会一个排一个,非常有秩序。然而,如果突然来了一个与队伍前面的人认识的人,这个人又不自觉,非要插队。那后面的人肯定要有意见了,说你要是这样我前面还有认识的人呢,你插我也插,这样整个队伍就乱掉了,谁也买不成。
通过这个例子,可得以下结论:彼此不认识,那就不相关,就有秩序,问题就好解决;反之,彼此相关,就没有秩序,问题就不好解决。所以,数学家们定义,矩阵中的最大的不相关的向量的个数,就叫秩,可以理解为有秩序的程度。
再比如说我们家中有很多张照片(N),但是一家只有三口(R),所以我们就把R当做矩阵的秩。

1、向量的内积
设有n维向量:$x=\begin{bmatrix}x_{1}\\ x_{2}\\ \vdots \\ x_{n}\end{bmatrix}$,$y=\begin{bmatrix}y_{1}\\ y_{2}\\ \vdots \\ y_{n}\end{bmatrix}$
$[x,y]=x_{1}\times y_{1}+x_{2}\times y_{2}+\cdots +x_{n}\times y_{n}$,此时我们就把$[x,y]$叫做向量的内积(也叫点乘,注意和外积(叉乘)的区别)。
性质:
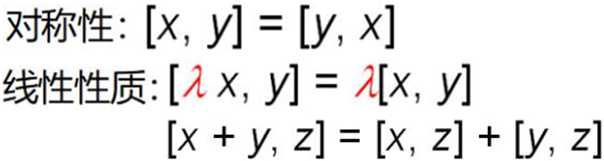
2、向量的长度
n维向量x的长度:$\left | x \right |=\sqrt{[x,x]}=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}\geqslant 0$。特别的,当|x|=1时称为单位向量。
齐次性:$\left | \lambda x \right |=\left | \lambda \right |\cdot \left | x \right |$。
三角不等式:$\left | x+y \right |\leqslant \left | x \right |+\left | y \right |$。
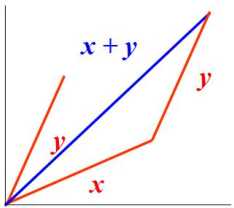
3、向量的正交。
两两正交的非零向量组成的向量组称为正交向量组。
若$\alpha _{1},\alpha _{2},\cdots ,\alpha _{r}$是两两正交的非零向量,则$\alpha _{1},\alpha _{2},\cdots ,\alpha _{r}$线性无关。
规范正交基,也叫标准正交基
n维向量$e_{1},e _{2},\cdots ,e_{r}$是向量空间$V\subset R^{n}$中的向量。满足:

则称$e_{1},e _{2},\cdots ,e_{r}$是V的一个规范正交基。例如$e_{1}=\begin{bmatrix}1\\ 0\\ 0\\ 0\end{bmatrix},e_{2}=\begin{bmatrix}0\\ 1\\ 0\\ 0\end{bmatrix},e_{3}=\begin{bmatrix}0\\ 0\\ 1\\ 0\end{bmatrix},e_{4}=\begin{bmatrix}0\\ 0\\ 0\\ 1\end{bmatrix}$是$R^{4}$的一个规范正交基
1、通俗理解
矩阵究竟做了什么?假如说让一个矩阵去乘以一个向量的话,那么矩阵对向量既可以做拉伸也可以做旋转,如下图所示
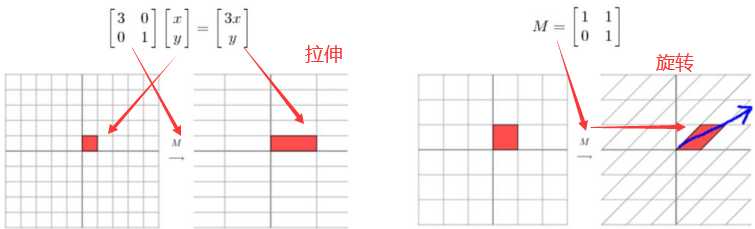
我们先来理解为什么叫特征值和特征向量,比如说有如下式子:
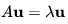
矩阵A当然是一个变换,然后这个变换的特殊之处是当它作用在特征向量 上的时候,
只发生了缩放变换,它的方向并没有改变,并没有旋转。就像 wikipedia 上经过了错切变换的蒙娜丽莎一样:

这幅图片在水平方向没有改变, $\begin{bmatrix}1\\ 0\end{bmatrix}$就是一个它的特征向量,对应的特征值是 λ = 1 。
再比如说在一次拳击比赛中, 拳击怎么赢?攻击的方向与力量,我们可以把方向当做是特征向量,在这个方向上用了多大的力量就是特征值。

2、数学定义
对于给定矩阵A,寻找一个常数λ和非零向量X,使得向量x被矩阵A作用后所得的向量AX与原向量X平行,并且满足AX=λX,那么这个X就是代表的特征向量了,λ代表的就是特征值了。
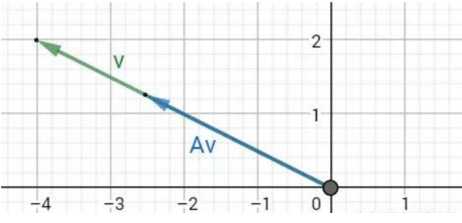
由所有的特征向量组成了特征空间
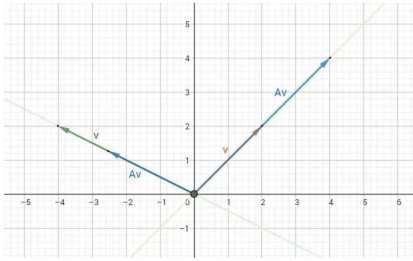
3、特征向量的应用
既然特征值表达了重要程度且和特征向量所对应,那么特征值大的就是主要信息了,基于这点我们就可以提取各种有价值的信息了。

数学基础系列(五)----矩阵、矩阵的秩、向量、特征值与特征向量
标签:方向 转换 tps size 作用 表达 target 元素 内容
原文地址:https://www.cnblogs.com/xiaoyh/p/12104263.html