基于贝叶斯的人脸验证

标签：com   idt   分类器   情况下   表示   strong   ash   观察   技术   

1. 贝叶斯分类的基础——贝叶斯定理

这个定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：

P(A|B)表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：

贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

下面不加证明地直接给出贝叶斯定理：

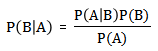
例如，医生对病人进行诊断就是一个典型的分类过程，任何一个医生都无法直接看到病人的病情，只能观察病人表现出的症状和各种化验检测数据来推断病情，这时医生就好比一个分类器，而这个医生诊断的准确率，与他当初受到的教育方式（构造方法）、病人的症状是否突出（待分类数据的特性）以及医生的经验多少（训练样本数量）都有密切关系。

2. Bayesian Face

基于贝叶斯的人脸验证

标签：com   idt   分类器   情况下   表示   strong   ash   观察   技术   

原文地址：https://www.cnblogs.com/zhaopengpeng/p/12186550.html