1. 几种相似度
1.1 Jaccard系数
杰卡德系数(Jaccard index) , 又称为Jaccard相似系数(Jaccard similarity coefficient),用于比较有限样本集之间的相似性与差异性。
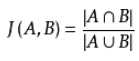
1.2 余弦相似度
余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。
对于二维空间,根据向量点积公式,显然可以得知:
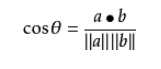
设向量 A = (A1,A2,...,An),B = (B1,B2,...,Bn) :
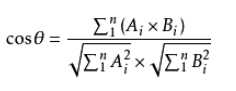
2. 相似度与距离
2.1 杰卡德距离和余弦距离的对比
杰卡德距离Jaccard distance(‘jaccard’)
Jaccard距离常用来处理仅包含非对称的二元(0-1)属性的对象。很显然,Jaccard距离不关心0-0匹配[1]。
夹角余弦距离Cosine distance(‘cosine’)
与Jaccard距离相比,Cosine距离不仅忽略0-0匹配,而且能够处理非二元向量,即考虑到变量值的大小。
对这两者,距离与相似度和为一。
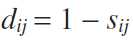
2.2 余弦距离和欧氏距离的对比
借助三维坐标系来看下欧氏距离和余弦距离的区别:
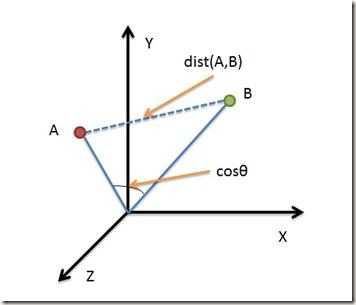
由图可知,相比欧氏距离,余弦距离更加注重两个向量在方向上的差异[2]。
更多距离参照[1]
2.3 以一例讲杰卡德距离。
有二物品A, B[3]。调查7为用户是否购买了这两样物品,得以下向量:
向量A:(0,0,1,1,1,0,1)
向量B:(1,0,1,0,1,0,0)
A∩B = 2

A∪B = 5
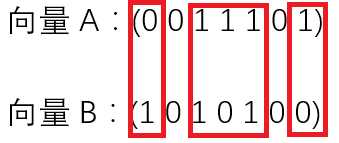
注意,因为忽略忽略0-0匹配。所以A∪B ≠ 7
3. 距离计算的MATLAB实现
matlab中自带的计算距离矩阵的函数有两个pdist和pdist2。
前者计算一个向量自身的距离矩阵,返回距离矩阵的下三角串联形式;后者计算两个向量之间的距离矩阵,返回是n*n的距离矩阵[4]。基本调用形式如下:
D = pdist(X,distance)
D = pdist2(X,Y,distance)
这两个函数都提供多种距离度量形式,非常方便,还可以调用自己编写的距离函数(distance可以用来表示其他距离,如果不写,默认的是欧式距离。)。
注意:计算的是行向量间的相互距离[5]
4. 两种距离的比较
对于行为相关性的度量,Jaccard一般效果更好;而对于文本相关性的度量,Cosine效果略好于Jaccard;但是Jaccard利于map/red计算。
更详细的介绍可以看文档[6]
[1] 使用Matlab计算各种距离Distance http://jacoxu.com/使用matlab计算各种距离distance/
[2] 余弦距离、欧氏距离和杰卡德相似性度量的对比分析 https://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html
[3] 分别用matlab和python计算物品相似度矩阵(Jaccard系数) http://blog.csdn.net/appleyuchi/article/details/71758783
[4]paper 120:计算距离矩阵的函数的pdist和pdist2函数 https://www.cnblogs.com/molakejin/p/5867255.html
[5]求5个向量两两之间的欧式距离 http://www.ilovematlab.cn/thread-308220-1-1.html
[6]推荐算法之Jaccard相似度与Consine相似度 http://blog.csdn.net/u010700335/article/details/72626997?locationNum=3&fps=1
