标签:接下来 href 位置 表示 inf box 手动 前置 博客
题目链接:LUOGU
题目描述:在一个 \(n\times m\) 的网格图中,每个格子里摆放着一个镜子,两种情况 /和\。
一个网格合法,当且仅当从任意一个边界段垂直射进网格中,光线会从相邻的边界段射出,同时网格中的每一段都被至少一条光线穿透。
现在网格中有 \(k\) 个位置的镜子形状不确定(用*表示),求合法网格数量\(\text{mod} \ p\)。
数据范围:\(n,m\le 100,k\le 200,3\le p\le 10^9+7\),\(p\) 为质数。
题解分析:首先你要知道什么叫对偶图(我觉得可能只有我之前不知道)
平面图大家都知道是什么了。
对偶图就是,对于一个平面图 \(G\),对偶图的点集就是 \(G\) 的面,两个点之间有边就是原图中两个面有公共边。
一个重要的性质:平面图的割与对偶图的简单环一一对应。
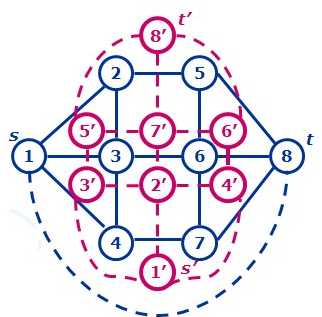
(图片来源:qzqzgfy的博客)
看这张图,\(s'\)到\(t'\)的路径可以把原图分为两个联通子集,也就是割。
上面是前置芝士,接下来我们考虑这道题。
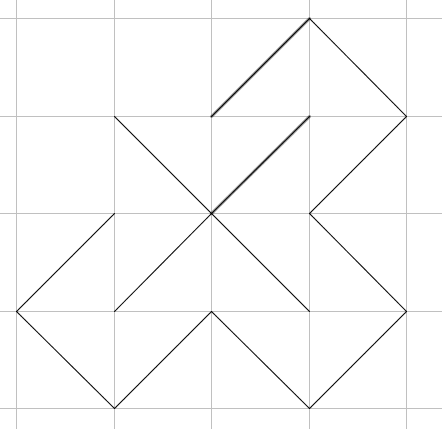
我们在这个图上加一些镜子,那么从左上角射入就又会从左上角射出,所以它的对偶图恰包含一个简单环,所以有一个割。然而如果对这个图黑白染色,那么每条边只会连接两个相同颜色的点。所以黑色点和白色点就是一个割。所以联通块个数为 \(2\)。
又因为点数\(=(n+1)(m+1)\),边数\(=mn+m+n-1\)(上面那张图加的镜子中每三条边实际上是一条边),所以联通块个数=点数-边数,所以整个图就是两棵树。其中一棵树是手动连起来的,另外一棵树是只靠原图中的边连起来的,所以答案就是黑色点组成树的方案数+白色点组成树的方案数(这张图只是两种情况中的一种)。先把确定的边连起来,再使用 Matrix-Tree 定理计算生成树个数。时间复杂度 \(O(nm\alpha(nm)+k^3)\)。
CF578F Mirror Box 【图论,Matrix-Tree】
标签:接下来 href 位置 表示 inf box 手动 前置 博客
原文地址:https://www.cnblogs.com/AThousandMoons/p/12188792.html