标签:style str div 原理 抽取 线性 multiple 通过 统一
多个数据文件的合并

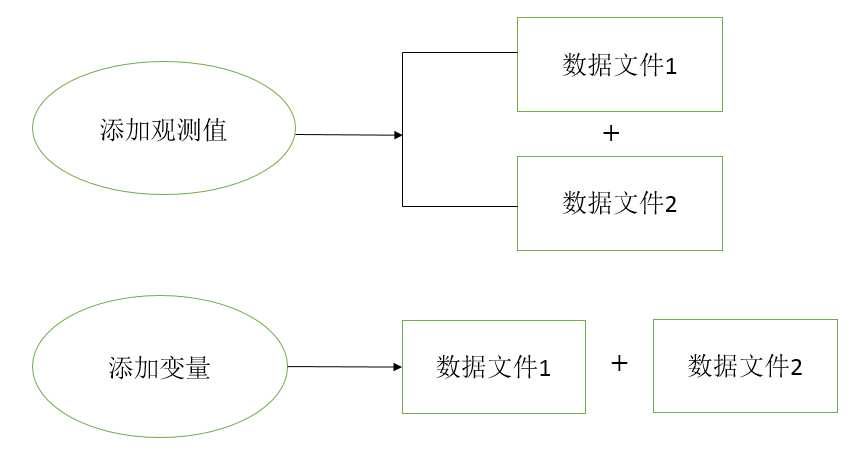
变量的合并

1.将带权重的问卷录入数据.sav中的权重变量添加到问卷录入数据(整理后).sav文件中,并尽量保留数据。
操作流程:数据——合并文件——添加变量
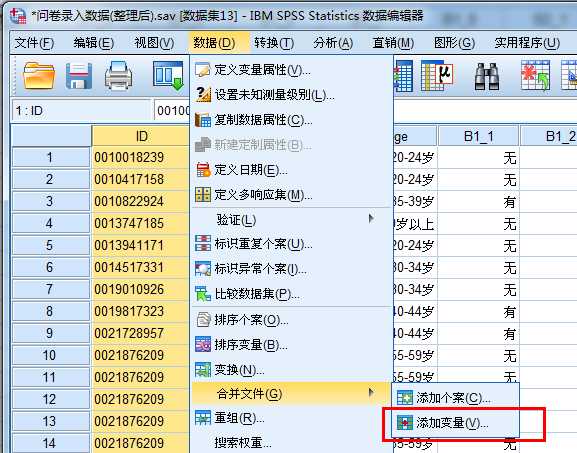
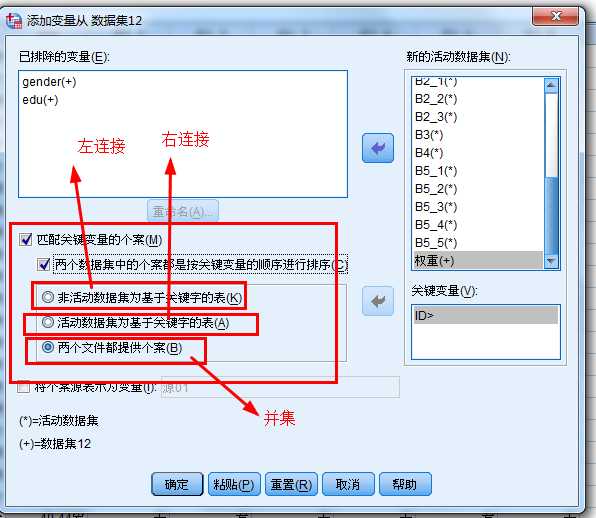
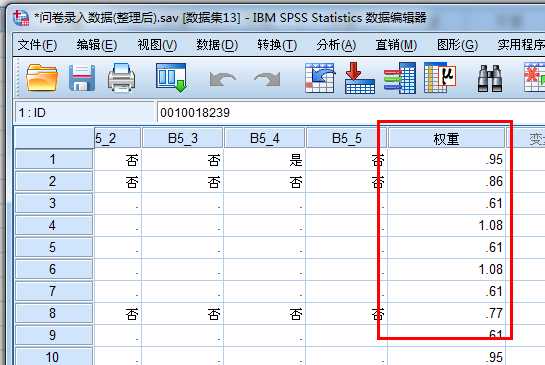
2. a.Sav包括了id号为偶数的5位受访者的性别、年龄和身高,c.sav则提供了4位受访者的体重,将
数据c.sav中的变量添加到a.sav中。(a是非活动集,c是活动集)
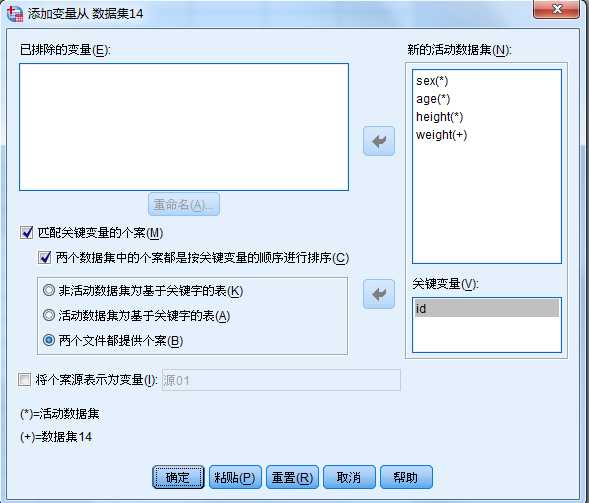
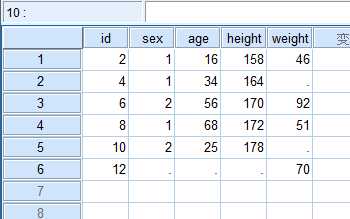

查看数据,右键单击,点击描述统计数据,然后

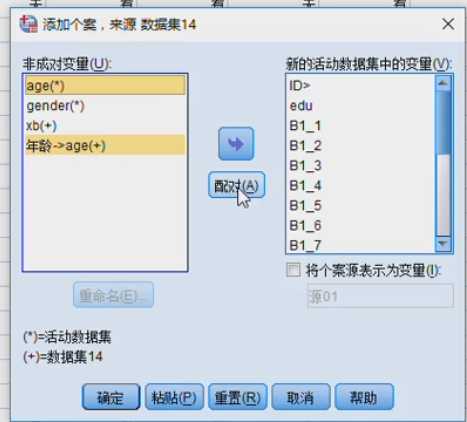

1.给定两个数据文件9月3日商品订购明细.sav和9月4日商品订购明细.sav,现在需要将两日的商品订购明细合并到一个数据集中。
2.将用户信息.sav中的变量添加到9月3日商品订购明细.sav中,并保留9月3日商品订购明细.sav中的全部数据。
主要内容:有时需要将一个数据文件分解,比如按照地区分析产品的销售情况,或者按照性别分析男女生的得分情况。
步骤:数据---拆分文件
案例文件:分类汇总练习某企业职工信息.sav
注意事项:数据的拆分并没有将总的文件拆分成几个分文件,而是在总文件中层次分明地显示出分文件。
SPSS预分析是进行其他统计分析的基础和前提。
通过基本统计方法的学习,可以对要分析数据的总体特征有比较准确的把握,从而有助于选择其他更为深入的统计分析方法。
第一章 频率分析
第二章 探索分析
第三章 相关分析
连续变量的频率分析:研究数值型数据
分类变量的频率分析:研究分类数据/顺序型数据
分类变量的频数分析
分析被调查者“所在的城市”和“性别”的频数分布调研数据.sav
分析被调查者“职业”和“婚姻状况”的频数分布调研数据.sav
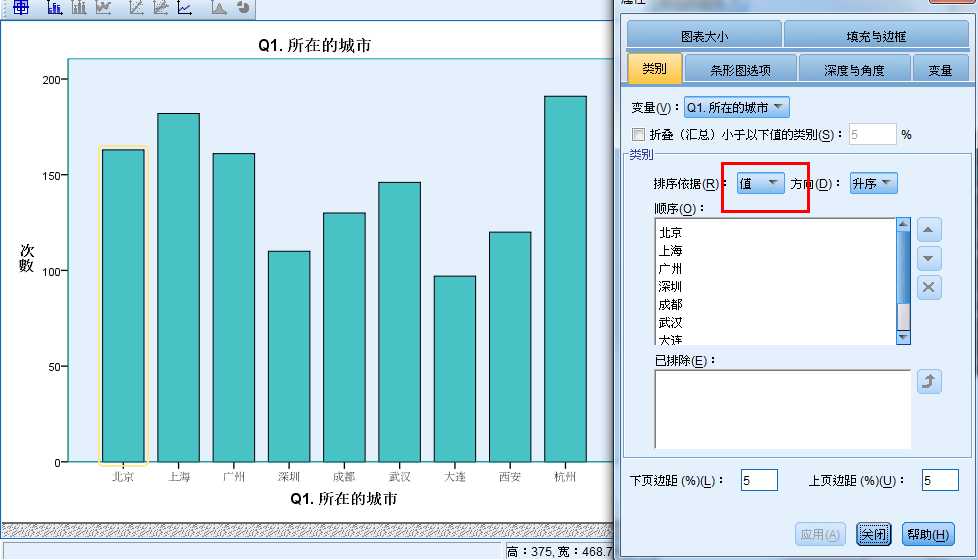
在输出文件进行 图形编辑 双击
选着标签,按首字母顺序排列
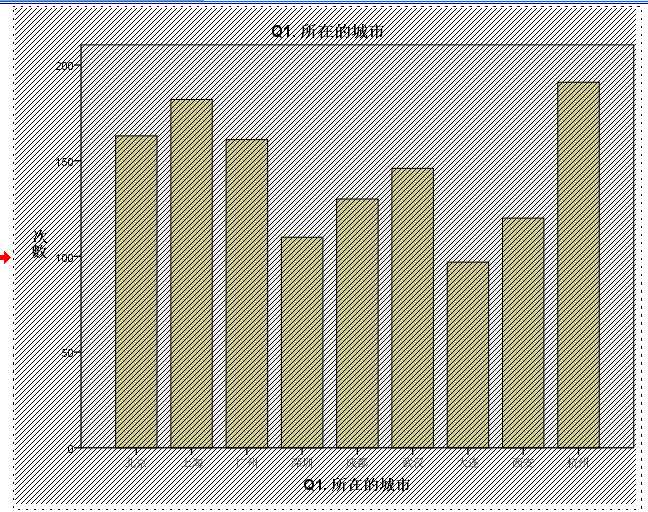
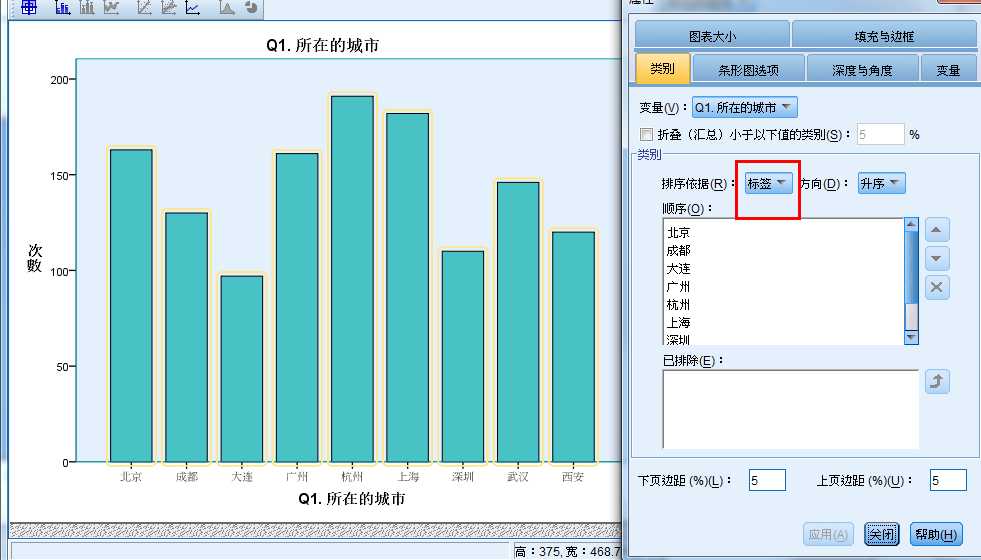
选着统计按 频数大小排列
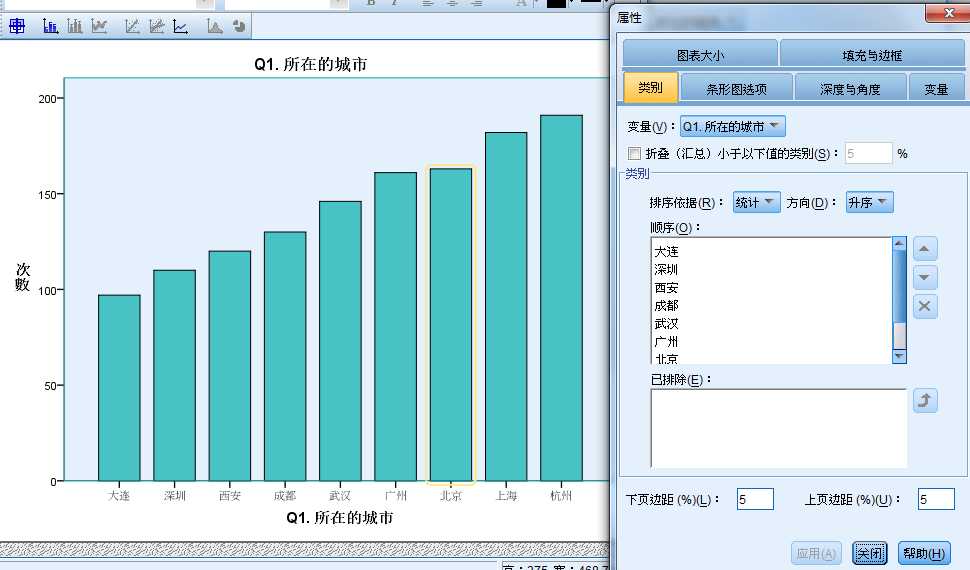
选着值 是按值标签排列的 例如 北京-1;上海--2
连续变量的统计描述从以下的几个方面:
集中趋势:大部分数值集中到某区间的趋势
离散趋势:数值向两边分散的趋势
分布形状(是否对称,分布曲线的形状)
分布特征(单、双峰,有无极端值等)

中位数、众数
全距
定义:全距也称为极差,是数据的最大值与最小值之间的绝对差。
在相同样本容量情况下的两组数据,全距大的一组数据要比全距小的一组数据更为分散。
计算公式:最大值-最小值。


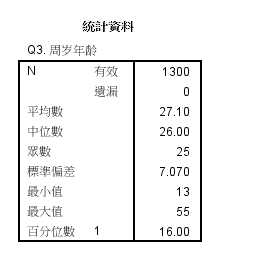
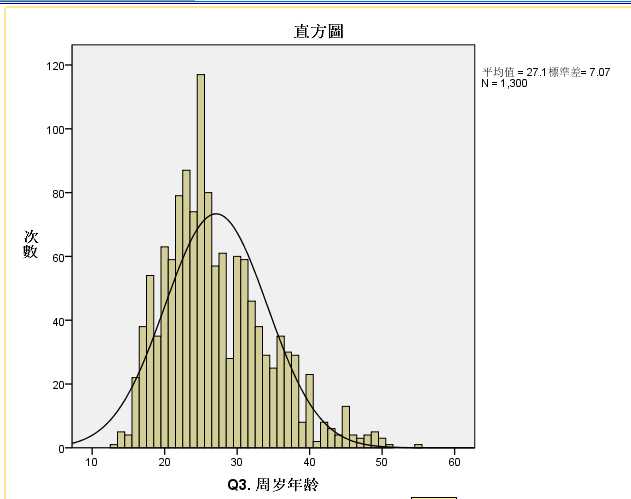
分析被调查者“周岁年龄”的最大值/最小值/平均值/众数/中位数/标准差/百分位数
数据:调研数据.sav
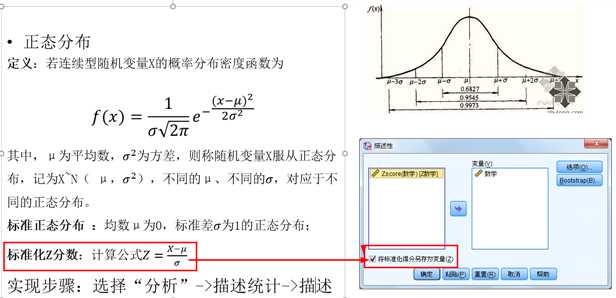
标准化的作用:统一量纲
3σ原则为
在正态分布中σ代表标准差,μ代表均值。x=μ即为图像的对称轴
3σ原则为
数值分布在(μ-σ,μ+σ)中的概率为0.6827
数值分布在(μ-2σ,μ+2σ)中的概率为0.9545
数值分布在(μ-3σ,μ+3σ)中的概率为0.9973
可以认为,Y 的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%.
标准化Z分数:在(-3,3)区间内
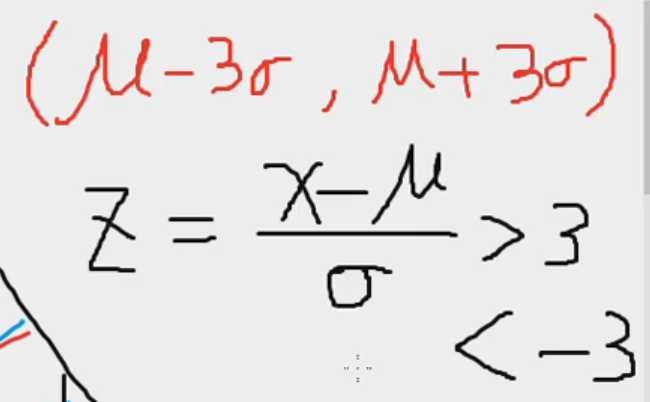
看某个数值型字段是否有异常值
例如:求年龄的标准化操作:
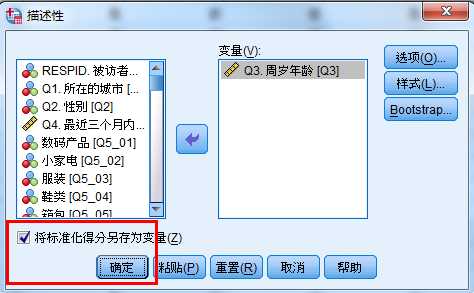
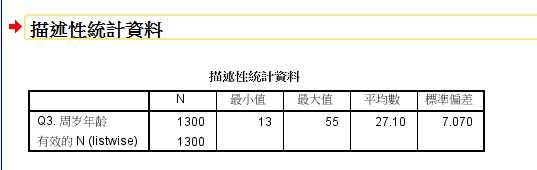
年龄异常值:
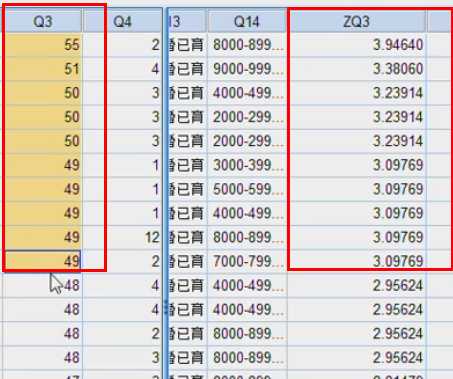
异常值处理-首先变成缺失值-再替换
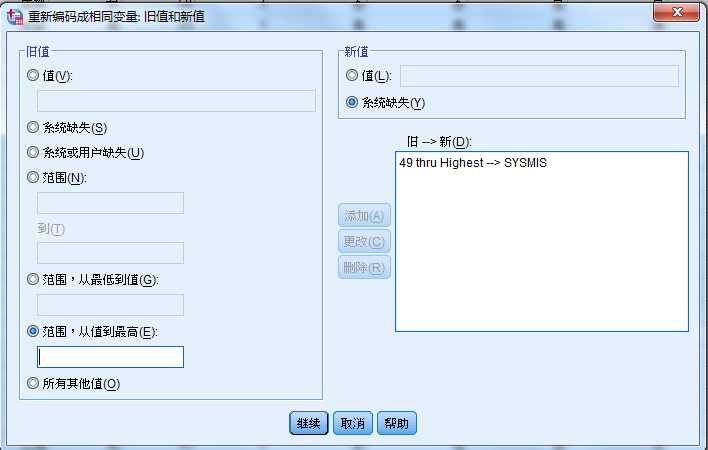
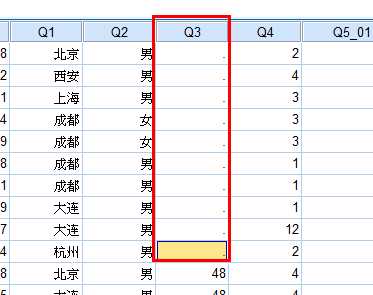
再做缺失值的替换
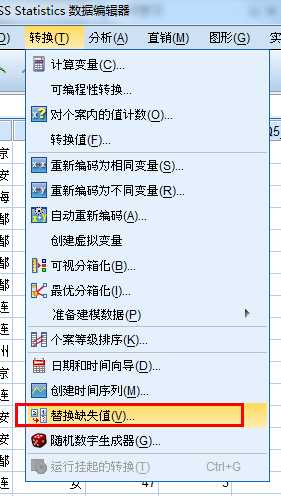
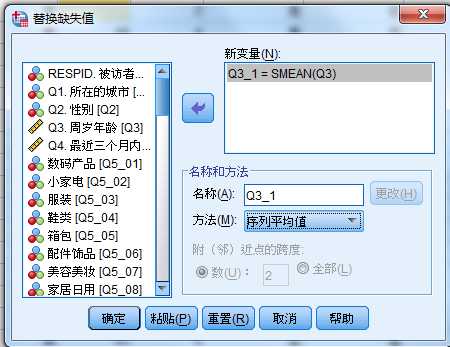
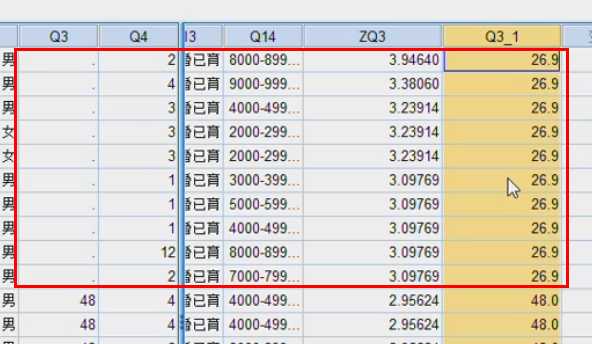

右偏,平均值>中位数>众数
左偏,平均值<中位数<众数

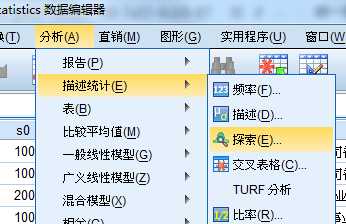
定义:调用此过程可对变量进行更为深入详尽的描述性统计分析,故称之为探索分析。
它在一般描述性统计指标的基础上,增加有关数据其他特征的文字与图形描述,显得更加细致与全面,有助于用户思考对数据进行进一步分析的方案。
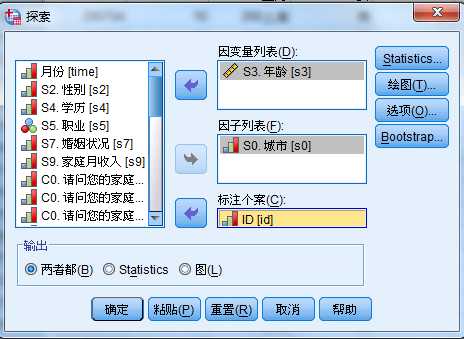
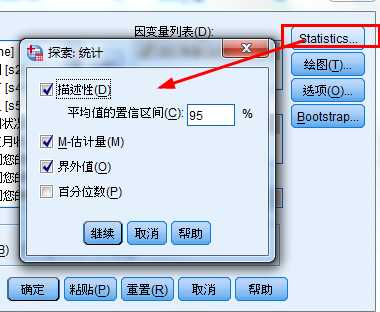
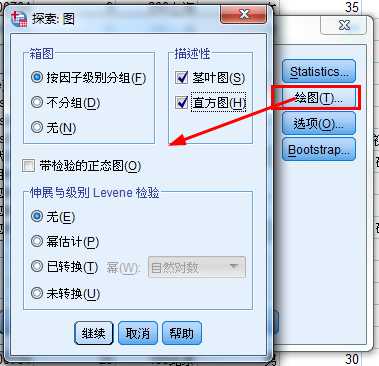
案例:
CCSS_Sample.sav, 用探索过程考察不同城市受访者年龄的分布情况。
茎叶图说明
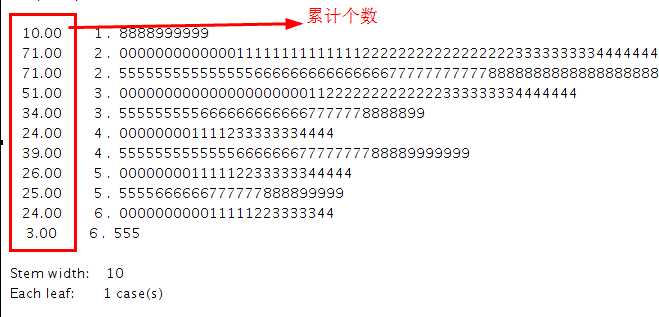
比如第二行的数字:
1 | 0 5 6 9,
它们代表数据集中有10、15、16和19四个数字。
可以这样理解茎+叶=实际的数值,如 1|0 5 6 9 中茎值为1,叶值为 0、5、6和9共四个叶值。
箱线图
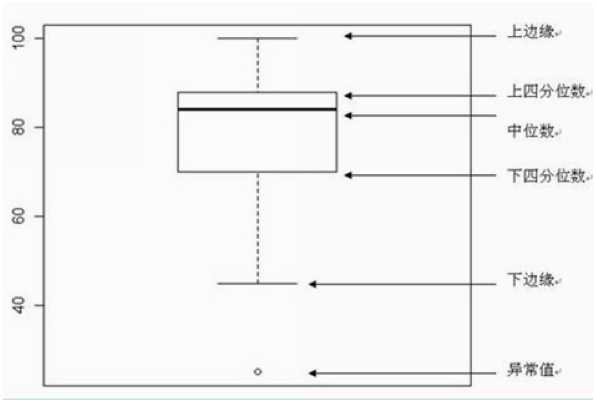
定义:前面的分析都是对单个变量的数据分布情况进行分析。
但在实际分析中,还需要掌握多个变量在不同取值情况下的数据分布情况,从而进一步深入分析变量之间的相互影响和关系,这种分析就称为交叉列联表分析。
用于两个或两个以上分组变量之间的关联关系。
研究问题:
不同性别的婚姻状况,数据调研数据.sav
操作流程:分析——描述统计——交叉表
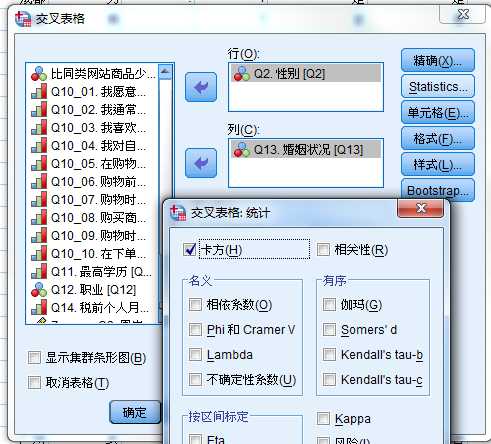
练习:
CCSS_Sample.sav,希望了解受访者的性别和学历交叉频数分布及百分比情况。
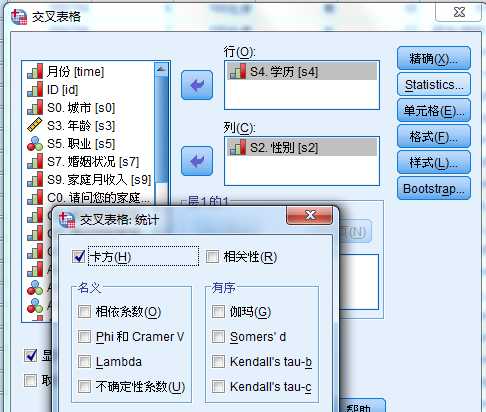
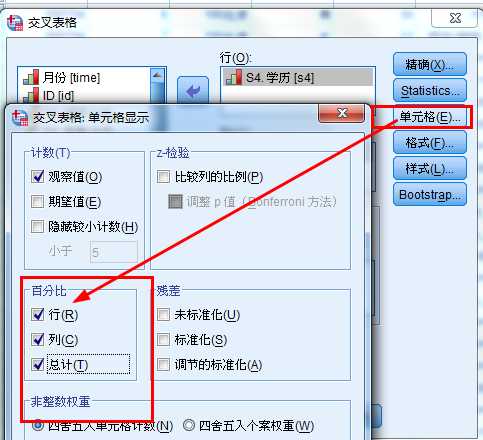
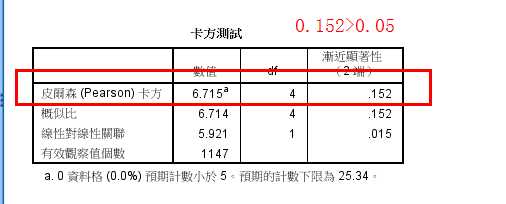
0.152>0.05 接受0假设;得出性别和学历没有关系

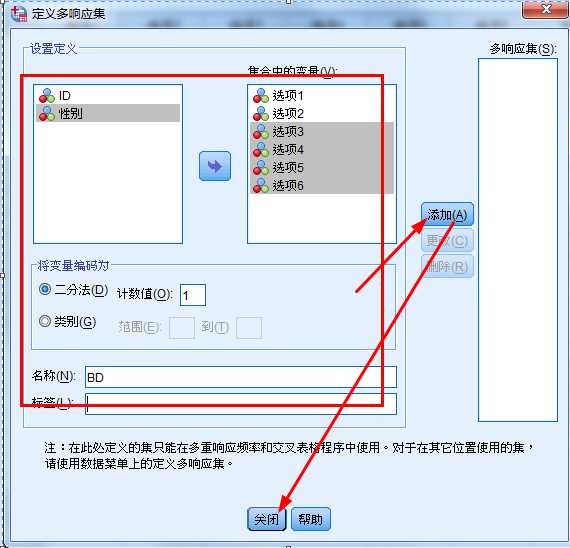
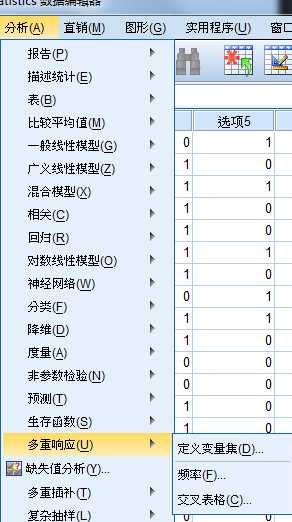
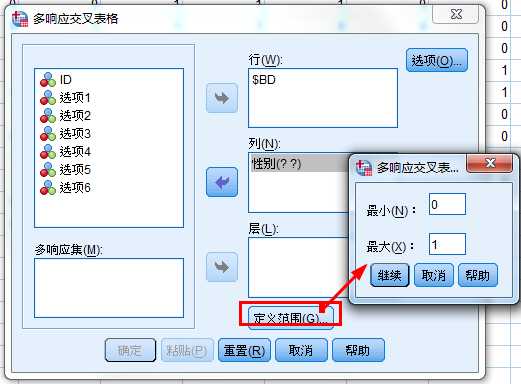
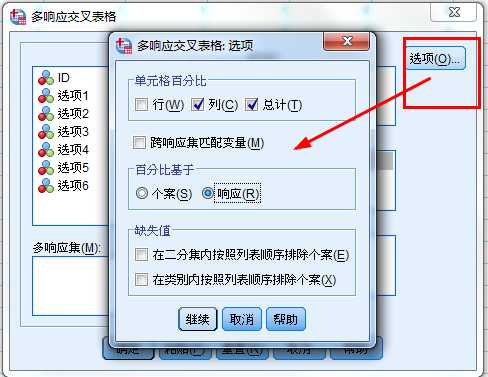
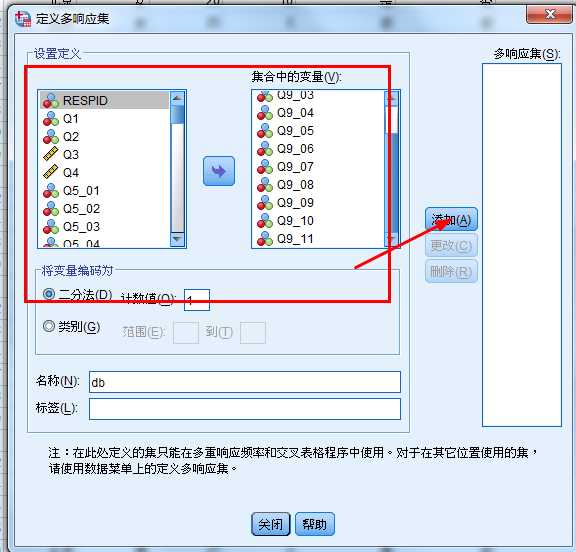
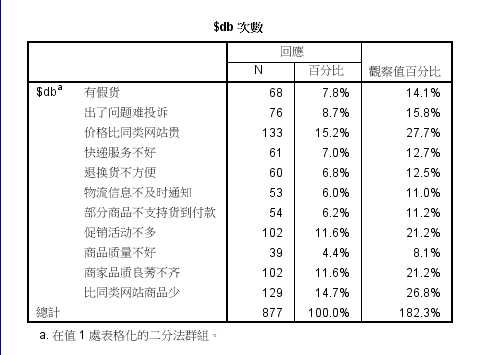
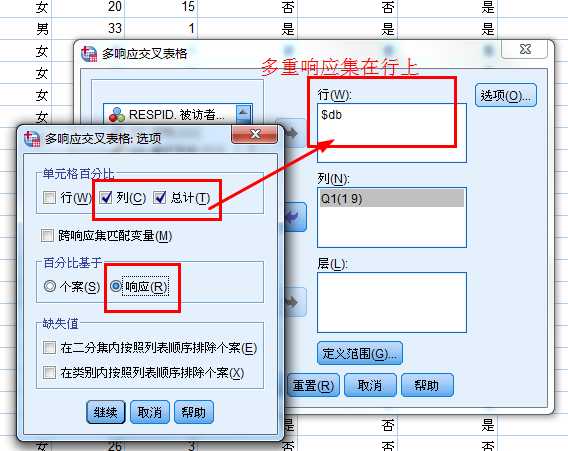
1.多选项二分法(Multiple Dichotomies Method)
2.多选项分类法(Multiple Category Method)

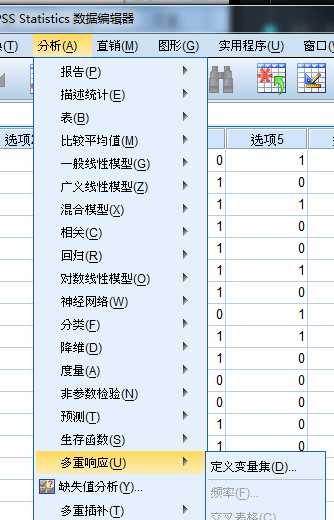

假设检验

假设检验
1、假设 2、检验
Step1、列出原假设,并默认原假设(无效假设)成立。
Step2、在原假设的条件下抽取样本,利用样本验证原假设的正确性。
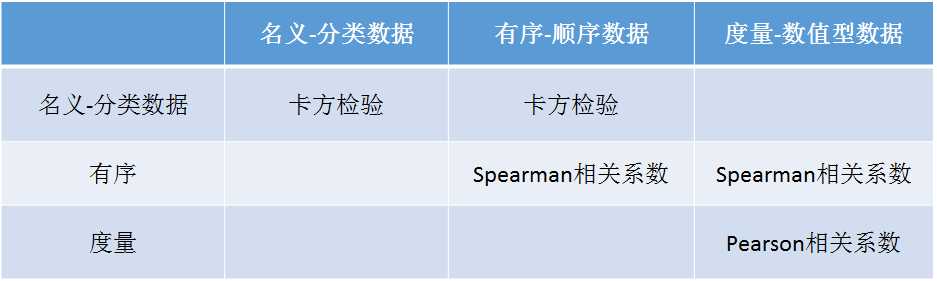
相关分析的方法原理:
分析步骤一般为:
绘制两个变量的散点图;
计算变量之间的相关系数;
相关系数的显著性检验。
SPSS相关系数检验的原假设为:
H0:|??| =0 ,两变量间无直线相关关系

在说明变量之间线性相关程度时,根据经验可将相关程度分为以下几种情况:
若|r|≥0.8 时,视为高度相关;
若0.5≤|r|<0.8 时,视为中度相关;
当0.3≤|r|<0.5时,视为低度相关;
当|r|<0.3时,说明变量之间的相关程度极弱,可视为不相关
相关系数:
表示变量间关系的密切程度,如果一个变量的取值发生变化,另外一个变量的取值也相应发生变化,则这两个变量有关。
散点图:呈现变量间的关联程度
如果对变量之间的相关程度不需要掌握得那么精确,可以通过绘制变量的相关散点图来直接判断。
案例文件 :CCSS_Sample.sav,利用相关分析考察总信心指数与家庭月收入S9的相关性。
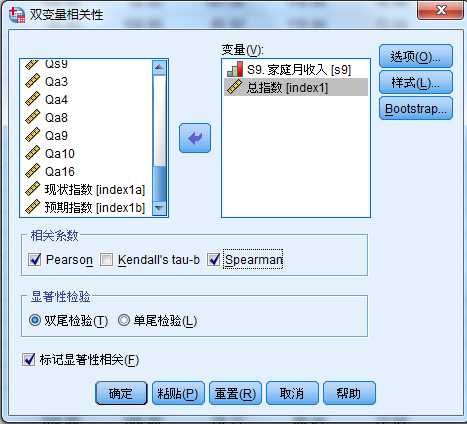
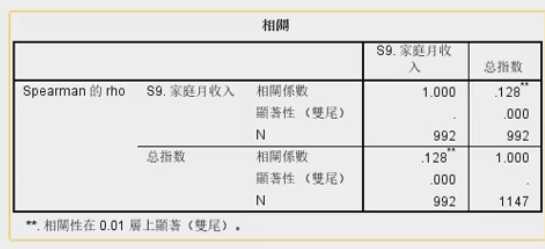
0.128>0.05 拒绝零假设 接受备选假设 即:信心指数与家庭月收入S9的相关性
案例文件 :CCSS_Sample.sav,前面的分析知道,家庭月收入对总信心指数是有影响的,
那么现在控制家庭月收入S9对总信心指数影响的前提下,考察总信心指数和年龄的相关性。

1111
标签:style str div 原理 抽取 线性 multiple 通过 统一
原文地址:https://www.cnblogs.com/foremostxl/p/12189740.html