标签:ddl 代码 isp img 定义 gre mamicode 说明 nes
本段代码可实现OLS法的线性回归分析,并可对回归系数做出分析
1.代码
%%OLS法下的线性回归
function prodict = Linear_Regression(X,Y)
x = sym(‘x‘);
n = max(size(X));
%%定义画图窗格属性
h = figure;
set(h,‘color‘,‘w‘);
%%回归相关值
XX_s_m = (X-Expection(X,1))*(X-Expection(X,1))‘;
XY_s_m = (X-Expection(X,1))*(Y-Expection(Y,1))‘;
YY_s_m = (Y-Expection(Y,1))*(Y-Expection(Y,1))‘;
%%回归系数
beta = XY_s_m/XX_s_m;
alpha = Expection(Y,1)-beta*Expection(X,1);
%%画出实际值与回归值的差
yyaxis left
for k = 1:n
delta_Y(k) = Y(k) - (alpha+beta*X(k));
end
width = (max(X)-min(X))/(2*n);
b = bar(X,delta_Y,width,‘Facecolor‘,[0.9 0.9 0.9]);
set(b,‘Edgecolor‘,‘none‘);
%标出差值
disp(‘是否标出差值?‘);
str = input(‘yes or no?‘,‘s‘);
Y_dis = (max(Y) - min(Y))/40;
if strcmp(str,‘yes‘) == 1
if n<=10
for k = 1:length(delta_Y)
if delta_Y(k)>=0
text(X(k),delta_Y(k)+Y_dis,strcat(num2str(delta_Y(k),‘%.3f‘)),...
‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);
else
text(X(k),delta_Y(k)-Y_dis,strcat(num2str(delta_Y(k),‘%.3f‘)),...
‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);
end
end
end
end
xlabel(‘X‘);ylabel(‘差值‘);
hold on
%%画出数据点
yyaxis right
plot(X,Y,‘g--*‘)
if n<=20
grid on;
end
hold on
ylabel(‘Y‘);
%%相关系数
R2 = (XY_s_m)^2/(XX_s_m*YY_s_m);
%%随机项方差无偏估计
sigma_2 = (Y*Y‘-n*Expection(Y,1)^2-beta*(X*Y‘-n*Expection(X,1)*Expection(Y,1)))/(n-2);
%%beta和alpha的方差
Var_beta = sigma_2/(X*X‘-n*Expection(X,1)^2);
Var_alpha = sigma_2*(X*X‘)/(n*(X*X‘-n*Expection(X,1)^2));
%%beta和alpha的协方差
cov_alpha_beta = -Expection(X,1)*sigma_2/(X*X‘-n*Expection(X,1)^2);
%%画出回归直线
x_v = min(X)-Expection(X,1)/sqrt(n):(max(X)-min(X))/100:max(X)+Expection(X,1)/sqrt(n);
y_v = beta*x_v+alpha;
y_ave = ones(1,max(size(x_v)))*Expection(Y,1);
plot(x_v,y_v,‘r‘,x_v,y_ave,‘k‘,‘LineWidth‘,0.2,‘LineStyle‘,‘-‘)
%%标出数据点
disp(‘是否标出数据点?‘);
str = input(‘yes or no?‘,‘s‘);
if strcmp(str,‘yes‘) == 1
if n <=10
for k = 1:max(size(X))
text(X(k),Y(k),[‘(‘,num2str(X(k)),‘,‘,num2str(Y(k)),‘)‘],...
‘color‘,‘b‘,‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);hold on;
end
end
end
disp(‘是否输出回归方程的置信区间?‘);
str = input(‘yes or no?‘,‘s‘);
if strcmp(str,‘yes‘) == 1
str = input(‘单侧置信系数 或者 双侧置信系数?‘,‘s‘);
if strcmp(str(1),‘单‘) == 1
ALPHA = input(‘输入单侧置信系数:‘);
a = 1-ALPHA*2;
elseif strcmp(str(1),‘双‘) == 1
ALPHA = input(‘输入双侧置信系数:‘);
a = 1-ALPHA;
end
disp(‘t(n-2)为:‘);
t_value = nctinv(a,n-2,0)
addvalue = t_value*sqrt(sigma_2)*sqrt(1+1/n+(x-Expection(X,1))^2/(X*X‘-n*Expection(X,1)^2));
disp(‘置信区间上限的方程为:‘);
vpa(alpha+beta*x+addvalue,4)
disp(‘置信区间下限的方程为:‘);
vpa(alpha+beta*x-addvalue,4)
y_ub = subs(alpha+beta*x+addvalue,x_v);
y_lb = subs(alpha+beta*x-addvalue,x_v);
plot(x_v,y_ub,‘--‘,x_v,y_lb,‘-.‘,‘color‘,[0.2 0.5 0.8]);
title(‘OLS法对数据的线性回归‘);
legend(‘差值‘,‘Y:实际值‘,‘y:拟合直线‘,‘平均值‘,‘置信上限‘,‘置信下限‘);
hold off
yyaxis left
text(min(X)-Expection(X,1)/sqrt(n),max(delta_Y)-Expection(delta_Y,1)/sqrt(n),[‘置信程度‘,num2str(100*a),‘%‘],‘color‘,[0.3 0.3 0.3]);
hold off
else
legend(‘差值‘,‘Y:实际值‘,‘y:拟合直线‘,‘平均值‘);
title(‘OLS法对数据的线性回归‘);
hold off
end
disp(‘是否输出回归系数的置信区间?‘);
str = input(‘yes or no?‘,‘s‘);
if strcmp(str,‘yes‘) == 1
str = input(‘单侧置信系数 或者 双侧置信系数?‘,‘s‘);
if strcmp(str(1),‘单‘) == 1
ALPHA = input(‘输入单侧置信系数:‘);
a = 1-ALPHA*2;
elseif strcmp(str(1),‘双‘) == 1
ALPHA = input(‘输入双侧置信系数:‘);
a = 1-ALPHA;
end
disp(‘t(n-2)为:‘);
t_value = nctinv(a,n-2,0)
disp(‘回归系数beta的置信区间为:‘);
[beta-t_value*sqrt(Var_beta),beta+t_value*sqrt(Var_beta)]
disp(‘回归系数alpha的置信区间为:‘);
[Expection(Y,1)-(beta+t_value*sqrt(Var_beta))*Expection(X,1),...
Expection(Y,1)-(beta-t_value*sqrt(Var_beta))*Expection(X,1)]
end
%%预测值输出
disp(‘是否需要求预测值?‘);
str = input(‘yes or no?‘,‘s‘);
if strcmp(str,‘yes‘) == 1
X0 = input(‘输入预测向量:‘);
str = input(‘单侧置信系数 或者 双侧置信系数?‘,‘s‘);
if strcmp(str(1),‘单‘) == 1
ALPHA = input(‘输入单侧置信系数:‘);
a = 1-ALPHA*2;
elseif strcmp(str(1),‘双‘) == 1
ALPHA = input(‘输入双侧置信系数:‘);
a = 1-ALPHA;
end
disp(‘t(n-2)为:‘);
t_value = nctinv(a,n-2,0)
addvalue0 = t_value*sqrt(sigma_2).*sqrt(1+1/n+(X0-Expection(X,1)).^2/(X*X‘-n*Expection(X,1)^2));
Y0 = alpha+beta*X0;
prodict{1,1} = {‘预测点x‘};
prodict{2,1} = {‘预测值y‘};
prodict{3,1} = {‘置信区间‘};
for k = 2:max(size(X0))+1
interval(k-1,:) = [Y0(k-1)-addvalue0(k-1),Y0(k-1)+addvalue0(k-1)];
prodict{1,k} = X0(k-1);
prodict{2,k} = Y0(k-1);
prodict{3,k} = interval(k-1,:);
Y0_lb(k-1) = Y0(k-1)-addvalue0(k-1);
Y0_ub(k-1) = Y0(k-1)+addvalue0(k-1);
end
h2 = figure(2);
set(h2,‘color‘,‘w‘);
plot(X0,Y0,‘r-*‘,X0,Y0_ub,‘g-o‘,X0,Y0_lb,‘b-o‘);hold on;
errorbar(X0,Y0,addvalue0,‘color‘,[0.8 0.5 0.2]);
xlabel(‘X‘);ylabel(‘y‘);
grid on;
title(‘点预测‘);
legend(‘预测值‘,‘置信上限‘,‘置信下限‘,‘置信限‘);
Y0_dis = (max(Y0)-min(Y0))/40;
Y0_lb_dis = (max(Y0_lb)-min(Y0_lb))/40;
Y0_ub_dis = (max(Y0_ub)-min(Y0_ub))/40;
disp(‘是否显示数据?‘);
str = input(‘yes or no?‘,‘s‘);
if strcmp(str ,‘yes‘) == 1
if max(size(X0)) <= 3
for k = 1:max(size(X0))
text(X0(k),Y0(k)+Y0_dis,[‘(‘,num2str(X0(k)),‘,‘,num2str(Y0(k)),‘)‘],...
‘color‘,[0.2 0.2 0.2]);hold on;
text(X0(k),Y0_lb(k)+Y0_lb_dis,[‘(‘,num2str(X0(k)),‘,‘,num2str(Y0_lb(k)),‘)‘],...
‘color‘,[0.2 0.2 0.2],‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);hold on;
text(X0(k),Y0_ub(k)+Y0_ub_dis,[‘(‘,num2str(X0(k)),‘,‘,num2str(Y0_ub(k)),‘)‘],...
‘color‘,[0.2 0.2 0.2],‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);hold on;
end
end
end
text(Expection(X0,1),(max(Y0)+max(Y0_ub))/2,[‘置信程度‘,num2str(100*a),‘%‘],‘color‘,[0.3 0.3 0.3]);
else
prodict = [];
end
disp(‘回归方程为:‘);
vpa(alpha+beta*x,4)
disp(‘相关系数平方为:‘);
vpa(R2,6)
disp(‘随机项方差的无偏估计为:‘);
vpa(sigma_2,6)
disp(‘回归系数beta和alpha的方差分别为:‘);
vpa(Var_beta,6)
vpa(Var_alpha,6)
disp(‘回归系数beta和alpha的协方差为:‘);
vpa(cov_alpha_beta,6)
%%SST,SSE和SSR
disp(‘SST:‘);
SST = YY_s_m
Y_OLS = reshape(alpha+beta*X‘,1,n);
disp(‘SSE:‘);
SSE = (Y_OLS-Expection(Y,1))*(Y_OLS-Expection(Y,1))‘
disp(‘SSR:‘);
SSR = (Y-Y_OLS)*(Y-Y_OLS)‘
function En = Expection(M,n) %%n阶原点矩%%
En = sum(M.^n)/size(M,2);
end
end
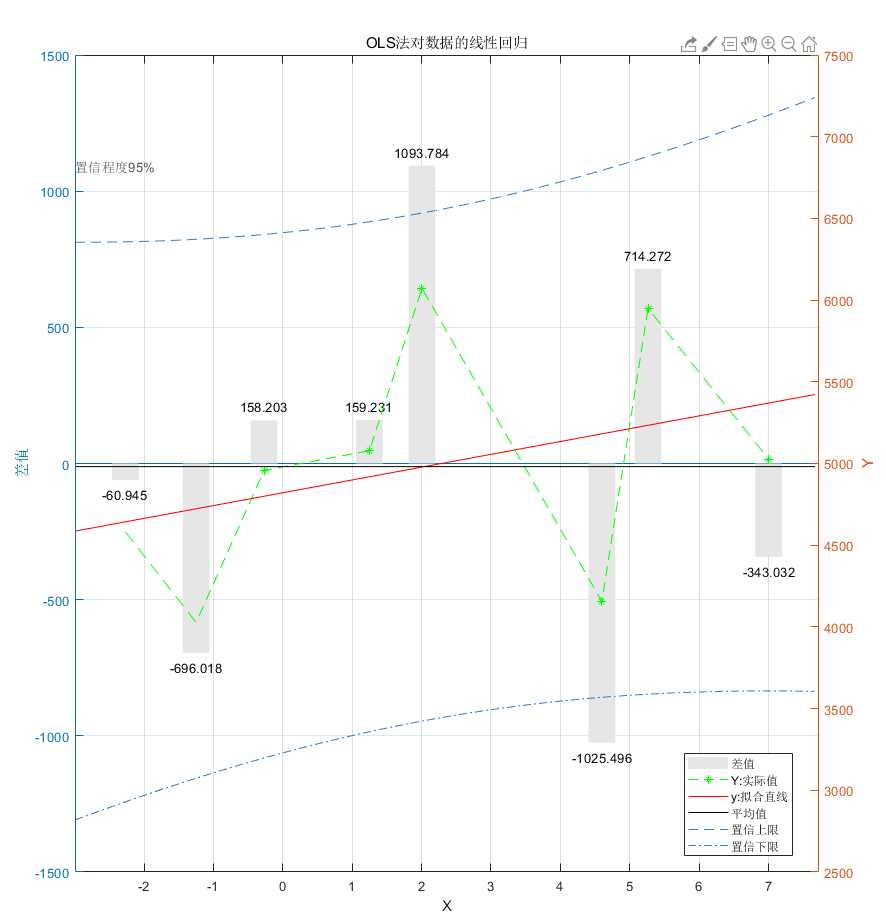
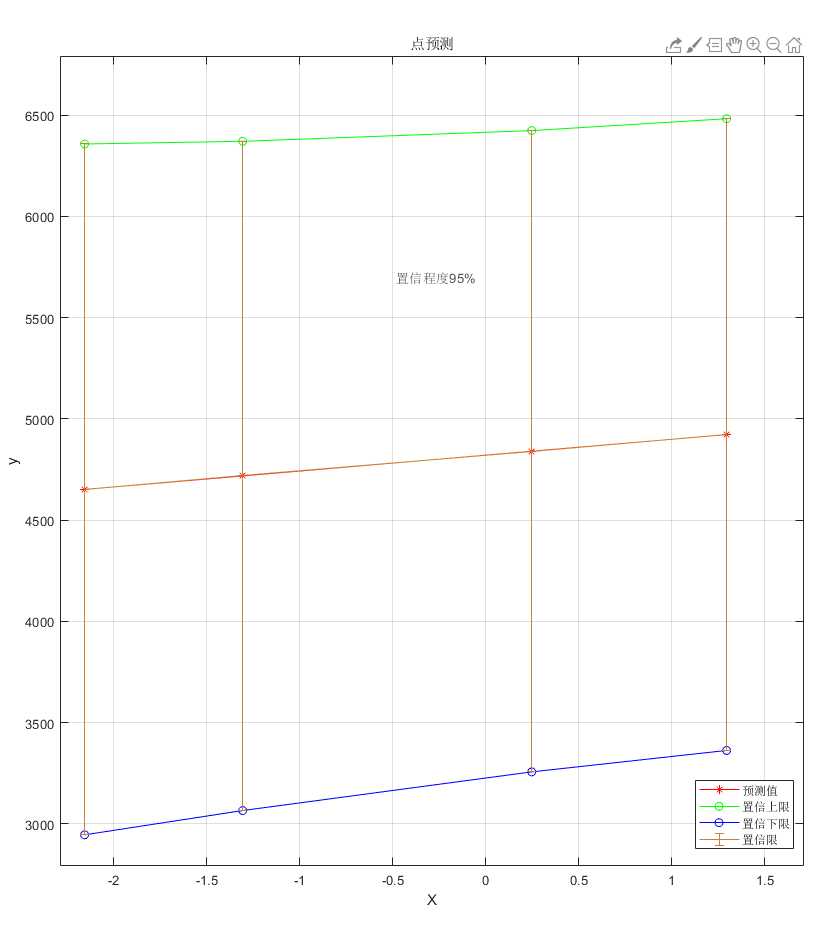
2.下面以一个例子来说明程序运行结果
clear all clc X = [-2.269 -1.248 -0.269 1.248 2.006 4.598 5.264 7.002]; Y = [4582 4027 4958 5078 6072 4156 5948 5027]; S = Linear_Regression(X,Y)
是否标出差值?
yes or no?yes
是否标出数据点?
yes or no?no
是否输出回归方程的置信区间?
yes or no?yes
单侧置信系数 或者 双侧置信系数?双
输入双侧置信系数:0.05
t(n-2)为:
t_value =
1.9432
置信区间上限的方程为:
ans =
78.43*x + 1466.0*(0.013*(x - 2.041)^2 + 1.125)^(1/2) + 4821.0
置信区间下限的方程为:
ans =
78.43*x - 1466.0*(0.013*(x - 2.041)^2 + 1.125)^(1/2) + 4821.0
是否输出回归系数的置信区间?
yes or no?yes
单侧置信系数 或者 双侧置信系数?双
输入双侧置信系数:0.05
t(n-2)为:
t_value =
1.9432
回归系数beta的置信区间为:
ans =
-88.7367 245.5885
回归系数alpha的置信区间为:
ans =
1.0e+03 *
4.4796 5.1622
是否需要求预测值?
yes or no?yes
输入预测向量:[-2.156 -1.306 0.248 1.296]
单侧置信系数 或者 双侧置信系数?双
输入双侧置信系数:0.05
t(n-2)为:
t_value =
1.9432
是否显示数据?
yes or no?no
回归方程为:
ans =
78.43*x + 4821.0
相关系数平方为:
ans =
0.121668
随机项方差的无偏估计为:
ans =
569067.0
回归系数beta和alpha的方差分别为:
ans =
7400.35
ans =
101976.0
回归系数beta和alpha的协方差为:
ans =
-15107.8
SST:
SST =
3887366
SSE:
SSE =
4.7297e+05
SSR:
SSR =
3.4144e+06
S =
3×5 cell 数组
列 1 至 4
{1×1 cell} {[ -2.1560]} {[ -1.3060]} {[ 0.2480]}
{1×1 cell} {[4.6518e+03]} {[4.7185e+03]} {[4.8403e+03]}
{1×1 cell} {1×2 double } {1×2 double } {1×2 double }
列 5
{[ 1.2960]}
{[4.9225e+03]}
{1×2 double }
%%OLS法下的线性回归function prodict = Linear_Regression(X,Y)x = sym(‘x‘);n = max(size(X));%%定义画图窗格属性h = figure;set(h,‘color‘,‘w‘);%%回归相关值XX_s_m = (X-Expection(X,1))*(X-Expection(X,1))‘;XY_s_m = (X-Expection(X,1))*(Y-Expection(Y,1))‘;YY_s_m = (Y-Expection(Y,1))*(Y-Expection(Y,1))‘;%%回归系数beta = XY_s_m/XX_s_m;alpha = Expection(Y,1)-beta*Expection(X,1);%%画出实际值与回归值的差yyaxis leftfor k = 1:n delta_Y(k) = Y(k) - (alpha+beta*X(k));endwidth = (max(X)-min(X))/(2*n);b = bar(X,delta_Y,width,‘Facecolor‘,[0.9 0.9 0.9]);set(b,‘Edgecolor‘,‘none‘);%标出差值disp(‘是否标出差值?‘);str = input(‘yes or no?‘,‘s‘);Y_dis = (max(Y) - min(Y))/40;if strcmp(str,‘yes‘) == 1 if n<=10 for k = 1:length(delta_Y) if delta_Y(k)>=0 text(X(k),delta_Y(k)+Y_dis,strcat(num2str(delta_Y(k),‘%.3f‘)),... ‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘); else text(X(k),delta_Y(k)-Y_dis,strcat(num2str(delta_Y(k),‘%.3f‘)),... ‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘); end end endendxlabel(‘X‘);ylabel(‘差值‘);hold on%%画出数据点yyaxis rightplot(X,Y,‘g--*‘)if n<=20 grid on;endhold onylabel(‘Y‘);%%相关系数R2 = (XY_s_m)^2/(XX_s_m*YY_s_m);%%随机项方差无偏估计sigma_2 = (Y*Y‘-n*Expection(Y,1)^2-beta*(X*Y‘-n*Expection(X,1)*Expection(Y,1)))/(n-2);%%beta和alpha的方差Var_beta = sigma_2/(X*X‘-n*Expection(X,1)^2);Var_alpha = sigma_2*(X*X‘)/(n*(X*X‘-n*Expection(X,1)^2));%%beta和alpha的协方差cov_alpha_beta = -Expection(X,1)*sigma_2/(X*X‘-n*Expection(X,1)^2);%%画出回归直线x_v = min(X)-Expection(X,1)/sqrt(n):(max(X)-min(X))/100:max(X)+Expection(X,1)/sqrt(n);y_v = beta*x_v+alpha;y_ave = ones(1,max(size(x_v)))*Expection(Y,1);plot(x_v,y_v,‘r‘,x_v,y_ave,‘k‘,‘LineWidth‘,0.2,‘LineStyle‘,‘-‘)%%标出数据点disp(‘是否标出数据点?‘);str = input(‘yes or no?‘,‘s‘);if strcmp(str,‘yes‘) == 1 if n <=10 for k = 1:max(size(X)) text(X(k),Y(k),[‘(‘,num2str(X(k)),‘,‘,num2str(Y(k)),‘)‘],... ‘color‘,‘b‘,‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);hold on; end endenddisp(‘是否输出回归方程的置信区间?‘);str = input(‘yes or no?‘,‘s‘);if strcmp(str,‘yes‘) == 1 str = input(‘单侧置信系数 或者 双侧置信系数?‘,‘s‘); if strcmp(str(1),‘单‘) == 1 ALPHA = input(‘输入单侧置信系数:‘); a = 1-ALPHA*2; elseif strcmp(str(1),‘双‘) == 1 ALPHA = input(‘输入双侧置信系数:‘); a = 1-ALPHA; end disp(‘t(n-2)为:‘); t_value = nctinv(a,n-2,0) addvalue = t_value*sqrt(sigma_2)*sqrt(1+1/n+(x-Expection(X,1))^2/(X*X‘-n*Expection(X,1)^2)); disp(‘置信区间上限的方程为:‘); vpa(alpha+beta*x+addvalue,4) disp(‘置信区间下限的方程为:‘); vpa(alpha+beta*x-addvalue,4) y_ub = subs(alpha+beta*x+addvalue,x_v); y_lb = subs(alpha+beta*x-addvalue,x_v); plot(x_v,y_ub,‘--‘,x_v,y_lb,‘-.‘,‘color‘,[0.2 0.5 0.8]); title(‘OLS法对数据的线性回归‘); legend(‘差值‘,‘Y:实际值‘,‘y:拟合直线‘,‘平均值‘,‘置信上限‘,‘置信下限‘); hold off yyaxis left text(min(X)-Expection(X,1)/sqrt(n),max(delta_Y)-Expection(delta_Y,1)/sqrt(n),[‘置信程度‘,num2str(100*a),‘%‘],‘color‘,[0.3 0.3 0.3]); hold offelse legend(‘差值‘,‘Y:实际值‘,‘y:拟合直线‘,‘平均值‘); title(‘OLS法对数据的线性回归‘); hold offenddisp(‘是否输出回归系数的置信区间?‘);str = input(‘yes or no?‘,‘s‘);if strcmp(str,‘yes‘) == 1 str = input(‘单侧置信系数 或者 双侧置信系数?‘,‘s‘); if strcmp(str(1),‘单‘) == 1 ALPHA = input(‘输入单侧置信系数:‘); a = 1-ALPHA*2; elseif strcmp(str(1),‘双‘) == 1 ALPHA = input(‘输入双侧置信系数:‘); a = 1-ALPHA; end disp(‘t(n-2)为:‘); t_value = nctinv(a,n-2,0) disp(‘回归系数beta的置信区间为:‘); [beta-t_value*sqrt(Var_beta),beta+t_value*sqrt(Var_beta)] disp(‘回归系数alpha的置信区间为:‘); [Expection(Y,1)-(beta+t_value*sqrt(Var_beta))*Expection(X,1),... Expection(Y,1)-(beta-t_value*sqrt(Var_beta))*Expection(X,1)]end%%预测值输出disp(‘是否需要求预测值?‘);str = input(‘yes or no?‘,‘s‘);if strcmp(str,‘yes‘) == 1 X0 = input(‘输入预测向量:‘); str = input(‘单侧置信系数 或者 双侧置信系数?‘,‘s‘); if strcmp(str(1),‘单‘) == 1 ALPHA = input(‘输入单侧置信系数:‘); a = 1-ALPHA*2; elseif strcmp(str(1),‘双‘) == 1 ALPHA = input(‘输入双侧置信系数:‘); a = 1-ALPHA; end disp(‘t(n-2)为:‘); t_value = nctinv(a,n-2,0) addvalue0 = t_value*sqrt(sigma_2).*sqrt(1+1/n+(X0-Expection(X,1)).^2/(X*X‘-n*Expection(X,1)^2)); Y0 = alpha+beta*X0; prodict{1,1} = {‘预测点x‘}; prodict{2,1} = {‘预测值y‘}; prodict{3,1} = {‘置信区间‘}; for k = 2:max(size(X0))+1 interval(k-1,:) = [Y0(k-1)-addvalue0(k-1),Y0(k-1)+addvalue0(k-1)]; prodict{1,k} = X0(k-1); prodict{2,k} = Y0(k-1); prodict{3,k} = interval(k-1,:); Y0_lb(k-1) = Y0(k-1)-addvalue0(k-1); Y0_ub(k-1) = Y0(k-1)+addvalue0(k-1); end h2 = figure(2); set(h2,‘color‘,‘w‘); plot(X0,Y0,‘r-*‘,X0,Y0_ub,‘g-o‘,X0,Y0_lb,‘b-o‘);hold on; errorbar(X0,Y0,addvalue0,‘color‘,[0.8 0.5 0.2]); xlabel(‘X‘);ylabel(‘y‘); grid on; title(‘点预测‘); legend(‘预测值‘,‘置信上限‘,‘置信下限‘,‘置信限‘); Y0_dis = (max(Y0)-min(Y0))/40; Y0_lb_dis = (max(Y0_lb)-min(Y0_lb))/40; Y0_ub_dis = (max(Y0_ub)-min(Y0_ub))/40; disp(‘是否显示数据?‘); str = input(‘yes or no?‘,‘s‘); if strcmp(str ,‘yes‘) == 1 if max(size(X0)) <= 3 for k = 1:max(size(X0)) text(X0(k),Y0(k)+Y0_dis,[‘(‘,num2str(X0(k)),‘,‘,num2str(Y0(k)),‘)‘],... ‘color‘,[0.2 0.2 0.2]);hold on; text(X0(k),Y0_lb(k)+Y0_lb_dis,[‘(‘,num2str(X0(k)),‘,‘,num2str(Y0_lb(k)),‘)‘],... ‘color‘,[0.2 0.2 0.2],‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);hold on; text(X0(k),Y0_ub(k)+Y0_ub_dis,[‘(‘,num2str(X0(k)),‘,‘,num2str(Y0_ub(k)),‘)‘],... ‘color‘,[0.2 0.2 0.2],‘VerticalAlignment‘,‘middle‘,‘HorizontalAlignment‘,‘center‘);hold on; end end end text(Expection(X0,1),(max(Y0)+max(Y0_ub))/2,[‘置信程度‘,num2str(100*a),‘%‘],‘color‘,[0.3 0.3 0.3]);else prodict = [];enddisp(‘回归方程为:‘);vpa(alpha+beta*x,4)disp(‘相关系数平方为:‘);vpa(R2,6)disp(‘随机项方差的无偏估计为:‘);vpa(sigma_2,6)disp(‘回归系数beta和alpha的方差分别为:‘);vpa(Var_beta,6)vpa(Var_alpha,6)disp(‘回归系数beta和alpha的协方差为:‘);vpa(cov_alpha_beta,6)%%SST,SSE和SSRdisp(‘SST:‘);SST = YY_s_mY_OLS = reshape(alpha+beta*X‘,1,n);disp(‘SSE:‘);SSE = (Y_OLS-Expection(Y,1))*(Y_OLS-Expection(Y,1))‘disp(‘SSR:‘);SSR = (Y-Y_OLS)*(Y-Y_OLS)‘
function En = Expection(M,n) %%n阶原点矩%% En = sum(M.^n)/size(M,2); endend
标签:ddl 代码 isp img 定义 gre mamicode 说明 nes
原文地址:https://www.cnblogs.com/guliangt/p/12202621.html