标签：key admin 分布 构建 path 其他 ref led rect
损失函数：
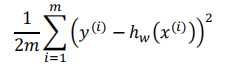
每次迭代使用所有样本来对参数进行更新。
损失函数：
代数形式：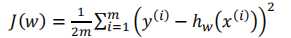
矩阵形式：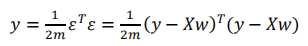
更新：
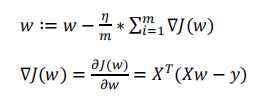
代数形式伪代码：
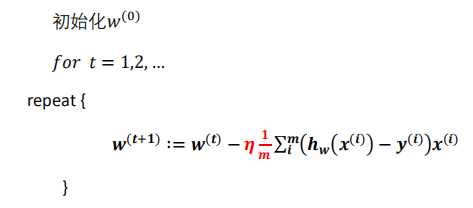
矩阵形式伪代码：
每次迭代使用一个样本来对参数进行更新。
一个样本的损失函数：
代数形式伪代码：
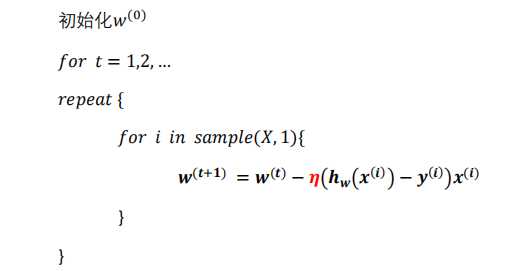
矩阵形式伪代码
# python
n_batch = 1
batch = np.random.choice(X.shape[0],n_batch)
X_batch,y_batch = X[batch], y[batch]
每次迭代使用n_batch个样本对参数进行更新
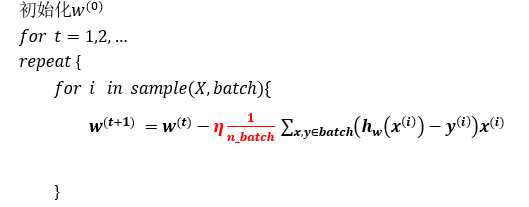
矩阵形式伪代码
n_batch = m
batch = np.random.choice(X.shape[0],n_batch)
X_batch,y_batch = X[batch], y[batch]
1. 线性目标的sgd优化，写出伪代码。mini_batch怎么更新？
2. SGD并行实现？
假设数据服从伯努利分布，通过极大似然函数的方法，用梯度下降来求解参数，来达到将数据分类，一般是二分类。
1. sigmoid函数推导
逻辑回归解决的是二分类问题，首先通过训练模型来学习x和y的映射关系，有了映射关系就容易对x和y进行预测分类。如何定义这种映射关系，这里假定y的取值为0或者1(也可以是其他类)，两种可能，自然而然服从伯努利分布，这种映射关系就可以通过条件概率p(y|x)来表示。p(y=1|x)和p(y=0|x)，对于二分类就可设定一个阈值，0.5。
如何通过条件概率来描述x和y之间的关系呢?对率回归是线性模型，但是无法直接表示成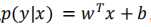
，那么就可以通过广义线性模型来实现。一般广义线性模型的一般形式， 
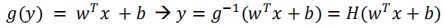，其中g(y)为单调函数，g(y)就可被作为联系函数。（为什么选择sigmoid函数，一般先考虑的是单位阶跃函数将任意的实数转换为0/1的概率值，用它来当成联系函数来判断属于哪个类。但是单位阶跃函数的一个缺点就是在零点不连续也不单调，而联系函数需要单调连续。）而sigmoid能够将(-无穷，+无穷)的值域映射到(0,1)，这样就可以得到合理的概率值，而且单调连续，可以作为联系函数。
这样就得到了
，将
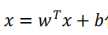代入，得到
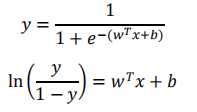
用条件概率表示就是
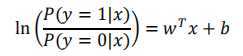
得到
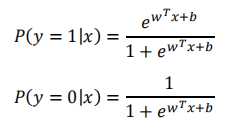
2. 广义线性模型推导
指数族分布：是一类分布的总称，它的概率密度函数一般形式是：
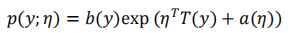
其中，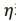
称为该分布的自然参数；T(y)为充分统计量，通常为y本身；
为配分函数，保证概率表达式加和为1，保证式子是合格的概率密度函数；b(y)是关于随机变量y的函数。常见伯努利和正态均为指数族分布。
证明：伯努利分布是指数族分布？
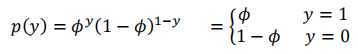
化成指数族的一般形式：
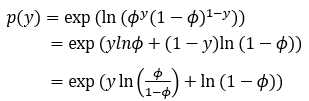
对应指数族分布的一般形式，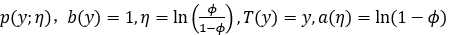
广义线性模型三假设：
1. 给定x的条件下，假设随机变量y服从指数族分布
2. 给定x条件下，目标是得到一个模型h(x)能预测出T(y)的期望值。
3. 假设该指数族分布中的自然参数和x呈线性关系，即
满足这三条假设即为广义线性模型。
对数几率回归是在对一个二分类进行建模，并假设被建模的随机变量y取值为0或1，可以很自然地假设y服从伯努利分布。如果想要构建一个线性模型来预测在给定x的条件下y取值的话，可以考虑使用广义线性模型来建模。
假设1：伯努利分布服从指数族分布。
假设2：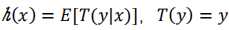
，得到
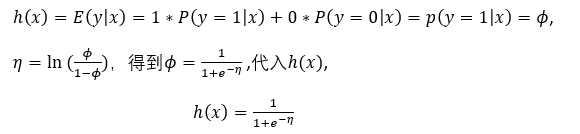
假设3：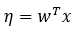
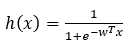
损失函数：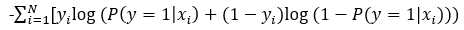 
由式子，
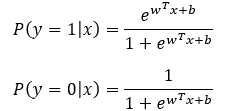
假设数据都是独立的，由伯努利分布，得到一个样本发生的条件概率表示为：
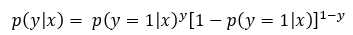
进而得到它们一起发生的概率（似然函数）：
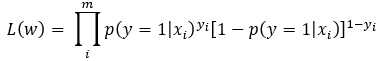
取对数，取负，得到损失函数
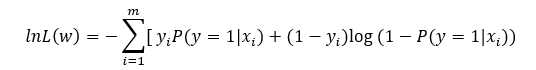
为什么用似然函数？
我们的目标是预测为某一类的出现概率最大，每个样本预测都要得到最大的概率。前面我们得到了一个样本的条件概率，极大似然估计就会将所有的样本考虑进去，来使得观测到的样本的出现概率最大，所以有了累乘形式的似然函数。 （为什么累乘？）基于条件独立的假设，总的条件概率就可以表示为每一个条件概率的累乘形式。
为什么用极大似然函数(交叉熵)作为损失函数而不用最小二乘（欧氏距离，均方损失）？
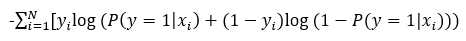
均方损失：假设误差是正态分布，适合线性的输出（回归问题），特点是对于与真实值差别越大，惩罚力度越大，不适合分类问题。
交叉熵损失：假设误差是伯努利分布，可以视为预测概率分布与真实概率分布的相似程度。多应用在分类的问题。
均方误差对参数的偏导的结果都乘以了 sigmoid的导数，而sigmoid导数在其变量值很大或很小时趋近于0，所以均方误差的偏导可能接近于0。
而参数更新公式： 参数 = 参数 – 学习率 * 损失函数对参数的偏导
在偏导很小时，参数更新速度会变得很慢，而在接近于0时，参数几乎不更新，出现梯度消失的情况。反观交叉熵对参数的偏导就没有sigmoid导数，所以不存在梯度消失的问题。
均方损失：
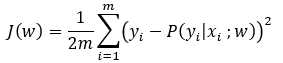
使用梯度下降法的条件损失函数时凸函数。而对最小二乘的损失函数求导，
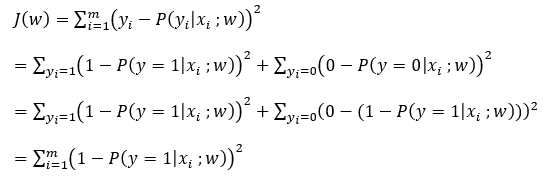
可以知道，J(w)对w不是凸函数，不能用代价函数。
交叉熵：
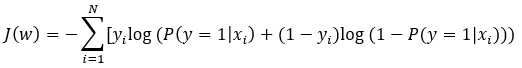
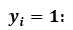
当越接近于1，越接近于0。预测值与真实值完全相同，其损失函数为0。
当越接近于0，越接近于。
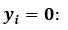
当越接近于1，越接近于。
当越接近于0，越接近于0。预测值与真实值完全相同，其损失函数为0。
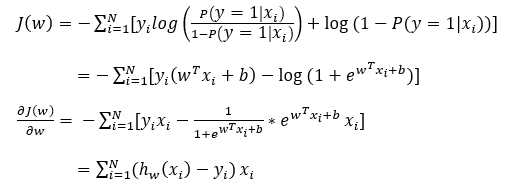
写成矩阵形式：
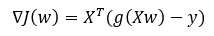
代数形式伪代码：
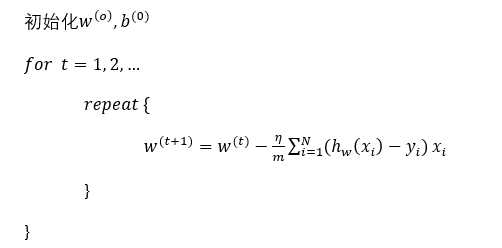
写在后，这是第一次写博客，平常喜欢在word或txt记录，也习惯了word的公式，就不打latex了，公式直接截图了。发出来的初衷有两个，一个是怕万一本地的文档像上个电脑突然去世，里面的资料都丢失了。还一个也是希望，对上述公式或者知识点是以个人的见解来总结或者直接拿过来，希望能够看到大家的看法，以及纠正，在这也对直接拿过来的这些原出处没办法做引用说明说声抱歉。
也是在自学的路上，更新会比较慢，这也是对自己的一种鞭挞吧。
后续，还会有想对牛顿法，拟牛顿法进行补充，在能够认为掌握之后。
愿正在阅读的你，以及仍热爱的你，共勉。
标签：key admin 分布 构建 path 其他 ref led rect
原文地址：https://www.cnblogs.com/bhc12/p/12203296.html
