标签:void cout $2 com 其它 str clu 怎么 sim
描述
一个长度为 $n$ 的好友列表,自上而下依次是 $1 \sim n$,你依次收到了 $m$ 条消息,第 $i$ 条消息是 $a_i$ 发来的,这时 $a_i$ 会跳到会话列表的最上面,其它的按原顺序顺延,求 $1 \sim n$ 每个好友最靠上的位置和最靠下的位置。
输入
第一行两个正整数 $n, m(1 \le n, m \le 3 \times 10^5)$。
第二行 $m$ 个正整数,描述序列 $a(a_i \in [1, n])$。
输出
$n$ 行,每行两个正整数,表示好友 $i$ 最靠上的位置和最靠下的位置。
样例
输入1
5 4
3 5 1 4输出1
1 3
2 5
1 4
1 5
1 5输入2
4 3
1 2 4输出2
1 3
1 2
3 4
1 4解释
在第一个样例中,会话列表的变化如下所示:
- $[1, 2, 3, 4, 5]$
- $[3, 1, 2, 4, 5]$
- $[5, 3, 1, 2, 4]$
- $[1, 5, 3, 2, 4]$
- $[4, 1, 5, 3, 2]$
例如,好友 $2$ 的位置依次是 $2, 3, 4, 4, 5$,最小值是 $2$,最大值是 $5$,所以答案为 $(2, 5)$。
在第二个样例中,会话列表的变化如下所示:
- $[1, 2, 3, 4]$
- $[1, 2, 3, 4]$
- $[2, 1, 3, 4]$
- $[4, 2, 1, 3]$
我们将答案分为两部分 $minn_i, maxx_i$,分别表示 $i$ 最靠前的位置和最靠后的位置。
这一部分是很好求的,因为,如果 $a$ 中出现了 $i$,那么 $minn_i$ 就必然是 $1$ 了(也就是 $i$ 刚发来消息时位置最靠前)。
如果 $i$ 从来没有发来消息的话,那 $minn_i$ 就是 $i$ 了,因为它一开始就在 $i$ 的位置,后来位置只可能往后,不可能往前。
首先,我们来回忆一下自己收到信息时的场景。
所以,我们发现,$i$ 的位置一定在他自己发来信息之前达到最大值!
也就是说,$i$ 的位置是这么一个函数:
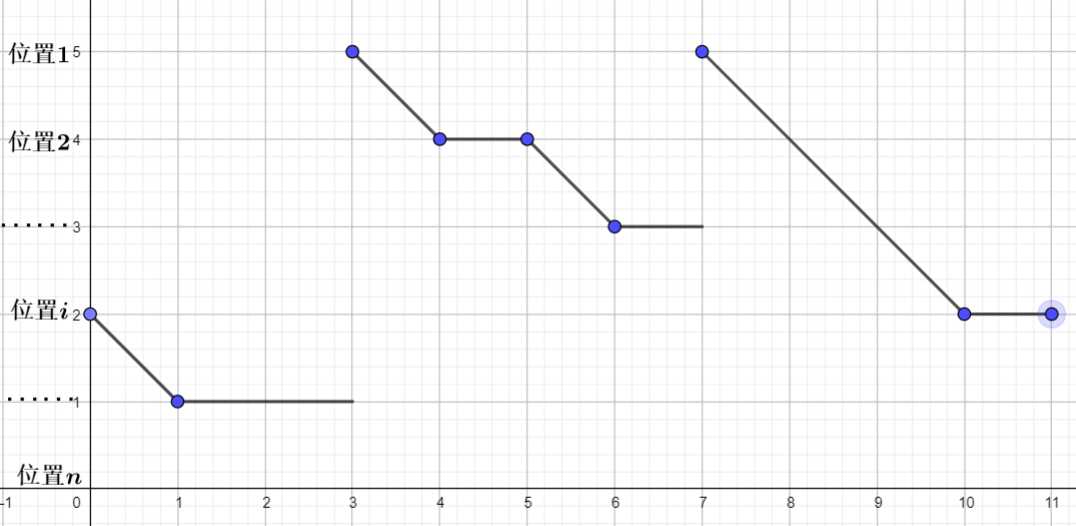
若干段 单调不上升函数!
那么,如果 $a_p = i$,$a_q = i$,并且中间没有 $i$ 了,则在 $q$ 时刻前 $i$ 的位置就是从 $a_p \sim a_{q - 1}$ 中 不同的数的个数。
还有一些麻烦的事情:比如 $i$ 出现了 $x$ 次,我们只处理了 $x - 1$ 个间隔的答案,那 $1 \sim$ 最先出现 $i$ 的位置,以及最后出现 $i$ 的位置 $\sim n$ 的答案怎么办呢?
后者十分容易处理:再数一遍 最后出现 $i$ 的位置 $\sim n$ 的不同的数字的个数即可。
前者我们不妨将上图中所示的第一段函数反向延长,使得其位置为 $1$(此时的 $x$ 坐标为 $-i + 1$),然后我们能不能构造一段新的 $a$,插在老 $a$ 的前面,使得达到我们想要的目的呢?
很显然,前面补上 $n \sim 1$ 这个长度为 $n$ 的序列就行了,然后对于原序列中最先出现 $i$ 的位置,只要数它和这个新添加的 $i$($n \sim 1$ 的序列中肯定有 $i$) 之间的不同的数字的个数即可。
考虑怎么统计不同的数字的个数。
如果采取莫队的方法,类比于 [国家集训队]数颜色,那时间复杂度是根号的,很悬。(但好像出题人 @pikmike 有意放这种做法过?)
考虑不带修改,那么就是可以用树状数组维护,类比于 [SDOI2009]HH的项链,可以在一个 $\log$ 的时间复杂度内解决这个问题!
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 5;
int n, m, cnt, a[N << 1], minn[N], maxx[N], lst[N];
struct tree_array // 树状数组相关
{
#define lowbit(x) x & -x
int o[N << 1];
tree_array() { memset(o, 0, sizeof o); }
int query(int p)
{
int res = 0;
for(; p; p -= lowbit(p)) res += o[p];
return res;
}
void modify(int p, int v)
{
for(; p <= n + m; p += lowbit(p)) o[p] += v;
}
} tr;
struct qry // 询问
{
int v, l, r; // 因为要离线,v 表示这个询问的结果用来更新 maxx[v]
bool operator < (const qry &oth) const { return r < oth.r; }
} q[N << 1];
void add_query(int v, int l, int r) { q[++cnt] = (qry){v, l, r}; }
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
for(int i = 1; i <= n; i++) a[n - i + 1] = i; // 构造 a
for(int i = 1; i <= m; i++) cin >> a[i + n];
for(int i = 1; i <= n; i++) minn[i] = maxx[i] = i;
for(int i = n + 1; i <= n + m; i++) minn[a[i]] = 1;
for(int i = 1; i <= n + m; i++)
{
if(!lst[a[i]]) lst[a[i]] = i;
else
{
add_query(a[i], lst[a[i]] + 1, i); // 添加两两之间的询问(自然包括了构造的部分)
lst[a[i]] = i;
}
}
for(int i = 1; i <= n; i++)
{
if(a[n + m] == i) continue; // 添加到末尾的询问
add_query(i, lst[i], n + m);
}
memset(lst, 0, sizeof lst);
sort(q + 1, q + cnt + 1);
// 处理离线后的每个询问
int now = 1;
for(int i = 1; i <= cnt; i++)
{
for(; now <= q[i].r; now++)
{
if(lst[a[now]]) tr.modify(lst[a[now]], -1);
lst[a[now]] = now;
tr.modify(now, 1);
}
maxx[q[i].v] = max(maxx[q[i].v], tr.query(q[i].r) - tr.query(q[i].l - 1));
}
for(int i = 1; i <= n; i++) cout << minn[i] << ‘ ‘ << maxx[i] << endl;
return 0;
}
CodeForces 1288E Messenger Simulator
标签:void cout $2 com 其它 str clu 怎么 sim
原文地址:https://www.cnblogs.com/syksykCCC/p/CF1288E.html