标签：个数   二维   状态   color   规模   blog   com   标准   ++   

旅行商问题描述

         现在有一个旅行商，在一个国家做生意。这个国家有N(2 <= N <= 15)个城市，城市之间有单行道可以通行，每条路都有相应的路费(0 <= d(I,j) <= 1000)。现在旅行商要从0号城市出发，经过所有的城市，最后回到0号城市。要求所花的路费最小。保证这些道路能构成一个环（可以一笔画）。

问题简化

         给出一张带权有向有环图，用邻接矩阵表示，d(i,j)表示ij两个节点之间边的权值，INF表示没有边。要求从0号节点出发，经过每一个节点后正好回到0号节点，问经过边的总权值最小是多少。

问题分析

         看到这道题，你的第一反应是不是暴力呀？嗯，很正常当时我也是这么想的。那我们不妨就来思考一下怎么暴力？其实呀，暴力就是一个全排列问题。把除0号节点外的所有节点全排列一遍，然后排除那些根本走不通的方案，最后在剩下的方案中找最小的花费。

         嗯。这种方案不是不行，时间复杂度是O((n-1)!)，在这里n最大是15，那最坏情况下的计算次数是87,178,291,200。超出了int的表示范围。但是这样还是可以骗分的。

进一步分析

其实这个问题是NP难问题。不能在多项式时间内进行求解。但是这种问题是可以用DP的思路来求解的。我们定义一个集合S，表示已经走过的节点的集合，定义集合V表示所有节点。再有v表示当前的节点。定义dp[S][v] 表示已走过节点为S，当前节点为v时，从v出发，经过~S的节点回到0号节点的最小花费。现在定义u表示下一步要走到的节点，。

可以得到递推式

状态压缩

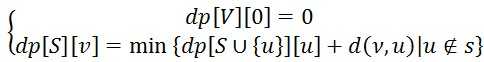
         我们发现，在dp这个数组中有一个维度是表示状态的集合。但我们又知道，数组的下标必须是整数，那怎么办呢？

         我们发现，一个节点要么在，要么不再S集合中。那么n个节点就可以表示成：“在、不在、在、不在S集合中”。再利用计算机二进制存储的特性，我们就可以把这种状态压缩到一个整数当中。而且我们发现N <= 15，也就是说这个表示状态的整数最大不过，就是65535，保证内存hold住。这种方法叫做状态压缩。

状压DP

         状压完了，就要开始DP了。DP最重要的条件是什么？最有子结构。这里的子结构一定是最优的（参见01背包的推导方法）。问题是怎么保证子结构呢？假设有两个压缩后的状态i,j，当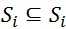时，i <= j。这就保证了一定能用循环求解。代码是这样的：

int dp[1 << MAX_N][MAX_N]; //DP数组

void solve() {
    //初始化
    for (int S = 0; S < 1 << n; ++S)
        for (int i = 0; i < n; ++i)
            dp[S][i] = INF;
    dp[(1 << n) - 1][0] = 0;
    
    //DP
    for (int S = (1 << n) - 2; S >= 0; S--) {
        for (int v = 0; v < n; ++v) {
            for (int u = 0; u < n; ++u) { //遍历u
                if (!(S >> u & 1)) //没有访问过
                    dp[S][v] = min(dp[S][v], dp[S | 1 << u][u] + d[v][u]);
            }
        }
    }
    
    cout << dp[0][0] << endl;
}

现在来解释一下。

         我们先假设S确定，来解释一下里面的循环。v循环是标准的DP循环，也可以参考01背包的解释。

         u循环的意思是遍历当当前节点是v时，下一步的走法。这时候你可能会产生疑问，为什么没有判断v u之间有没有边。因为如果v u之间没有边，那v u之间的距离就是INF，是不会被min选中的。

         min判断的前面表示不选u节点作为下一步，后面表示往后走一步。其实就是找最小值。自己理解一下。

         然后我们来理解一下S循环。你可能会产生疑问，为什么S要逆序。01背包逆序是要防止数据的覆盖，但是这本来就是二维数组，不存在这种问题。

　　要解释这个问题，我们就要先回顾一下动态规划的基本思路，就是有小规模的问题合并成大规模的问题。那什么是小规模的问题？是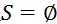吗？当然不是，如果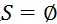的话，就是一个点也没有走，这应该是最后要求解的答案（回顾一下dp[S][v]的定义）。规模最小的问题应该是已经走过了其他所有的点，就差一步就回到0号节点的状态，就是(1 << n) – 2。因为已知dp[V][0]=0，所以这种DP是可行的。

旅行商问题 状压DP

标签：个数   二维   状态   color   规模   blog   com   标准   ++   

原文地址：https://www.cnblogs.com/Iuppiter/p/12208687.html