数据通信的基础知识

标签：数据显示   取值   时间间隔   振幅   容量   应用   距离   github   通信   

数据通信的基础知识

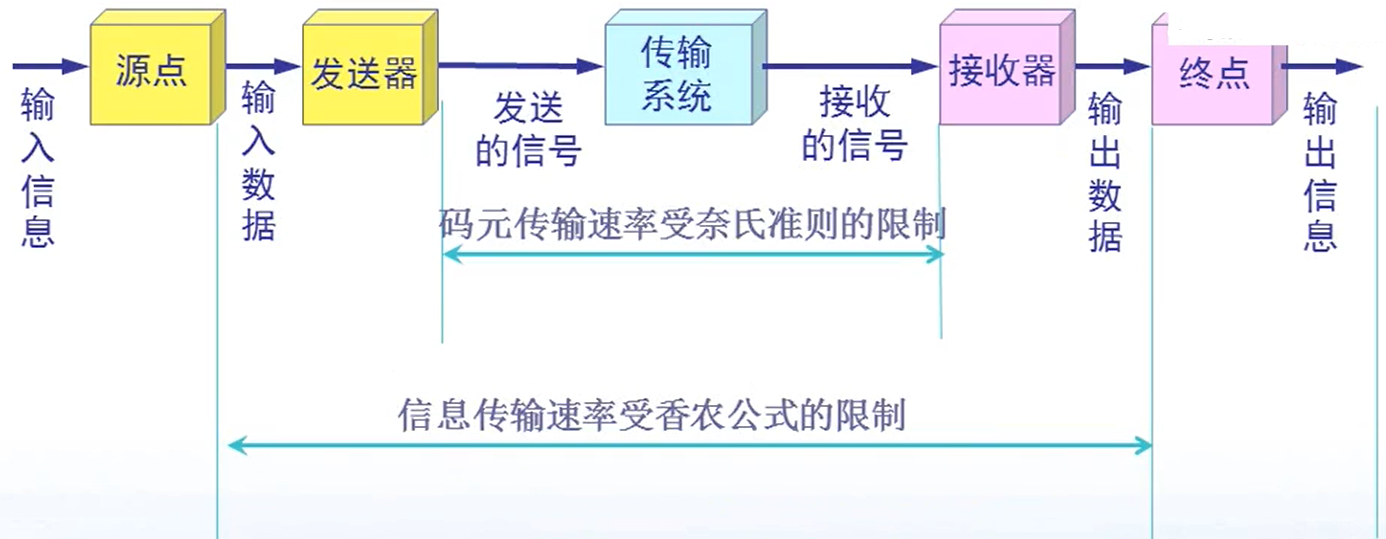
典型的数据通信模型：

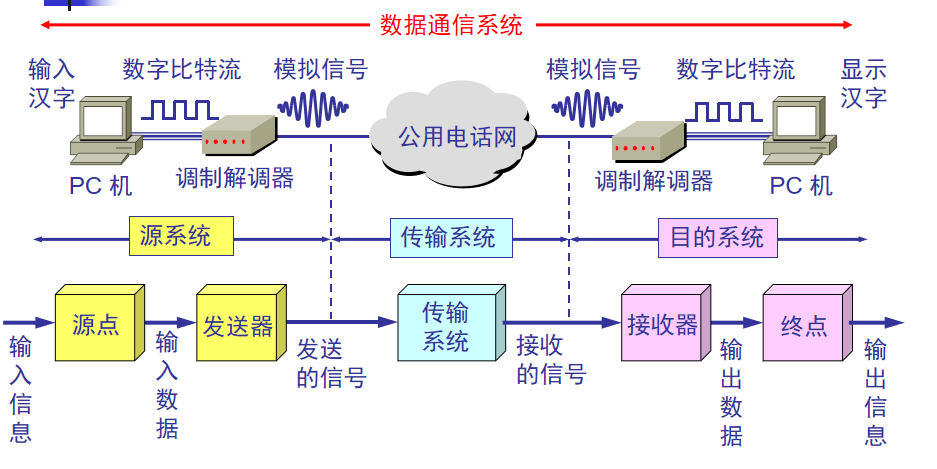
相关术语

通信的目的是传送消息。

• 数据（data）——运送消息的实体；
• 信号（signal）——数据的电气或电磁的表现；
  • “数字信号”——代表消息的参数的取值是离散的；
  • “模拟信号”——代表消息的参数的取值是连续的；
• 码元（code）——在使用时间域的波形标识数字信号时，则代表不同离散数值的基本波形就形成了码元；

在数字通信中常常使用时间间隔相同的符号来表示一个二进制数字，这样的时间间隔内的信号称为二进制码元。而这个间隔被称为码元长度。1码元长度可以携带nbit的信息量。

有关信道的几个基本概念

信道一般表示向一个方向传送信息的媒体。所以通信线路往往包含一条发送消息的信道和一条接收信息的信道。

• 单向信道（单工通信）——只能有一个方向的通信而没有反方向的交互；比如电台广播；
• 双向交替通信（半双工通信）——通信的双方都可以发送消息，但不能双方同时发送（当然也就不能同时接收）；比如对讲机；
• 双向同时通信（全双工通信）——通信的双方可以同时发送和接收数据；比如打电话；

基带（baseband）信号和带通（band pass）信号

• 基带信号（即基本频带信号）——来自信源的信号。像计算机输出的代表各种文字或图像文件的数据信号都属于基带信号。基带信号就是发出的直接表达了要传输的信息的信号，比如我们说活的声波就是基带信号。
• 带通信号——把基带信号经过载波调制后，把信号的频率范围搬移到较高的频段以便在信道中传输（即仅在一段频率范围内能够通过信道）。

由于在近距离范围内基带信号的衰减不大，从而信号内容不会发生变化。因此在传输距离较近时，计算机网络都采用基带传输方式。例如计算机到监视器、打印机等外设的信号就是基带传输的。

几种基本的调制方法

• 调幅（AM）：载波的振幅随基带数字信号而变化；
• 调频（FM）：载波频率随基带数字信号而变化；
• 调相（PM）：载波的初始相位随基带数字信号而变化；

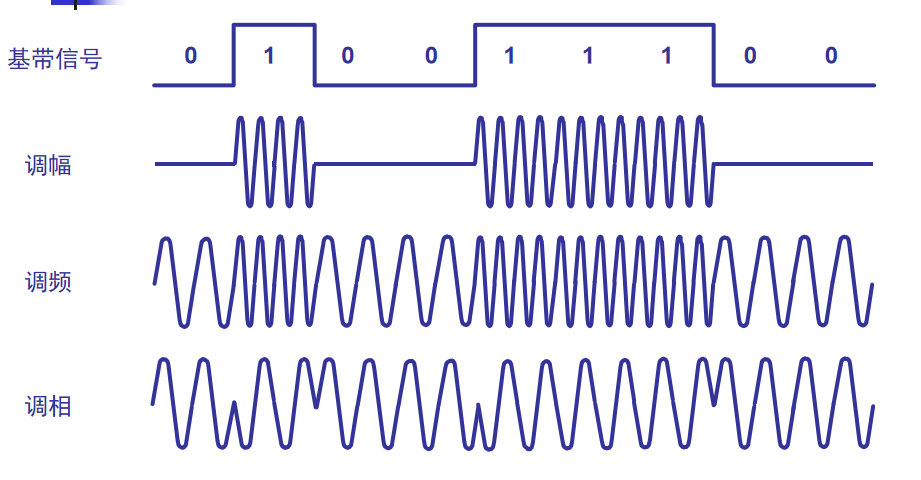
常用编码

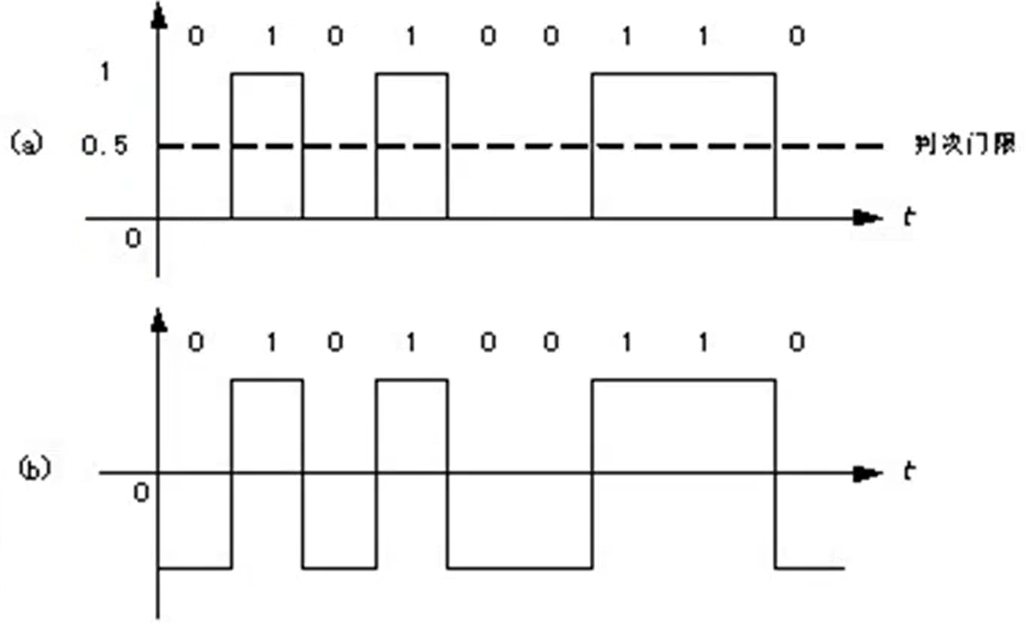
• 单极性不归零码：只是用一个电压值，用高电平表示1，没电压表示0，下图（a）；

• 双极性不归零码：用正电平和负电平分别表示二进制的1和0，正负幅值相等，下图（b）；

• 双极性归零码：正负零三个电平，信号本身携带同步信息；

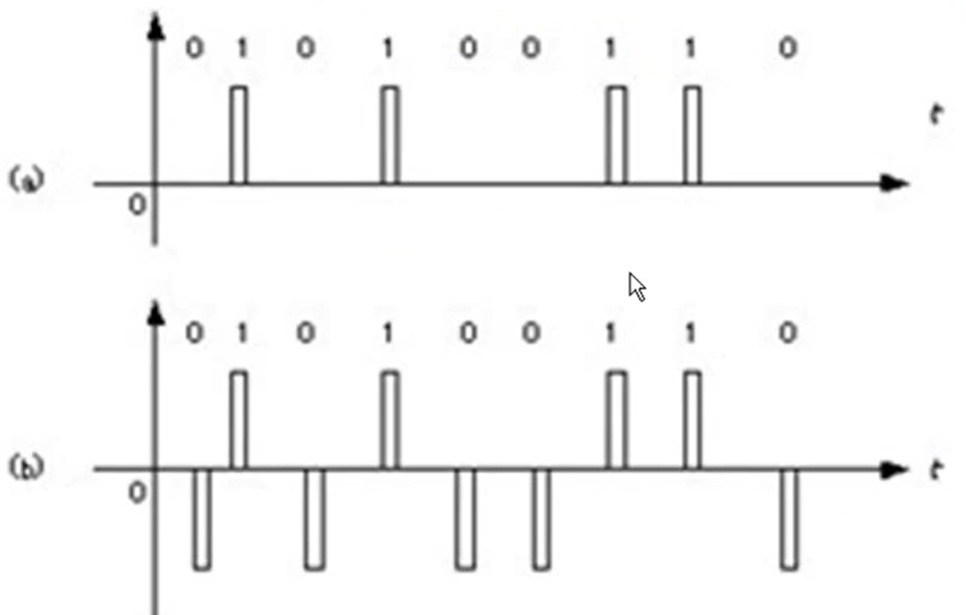
（a）为单极性归零码；（b）为双极性归零码0

以上编码方式的缺点为：接收端无法判断数据传输是否结束。即数据尾部的0是有效数据还是没数据显示的没意义的0.

• 曼彻斯特编码

该编码方式完善了上述编码方式的缺点。

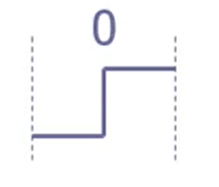
• bit中间有信号，低——高跳变为0

  

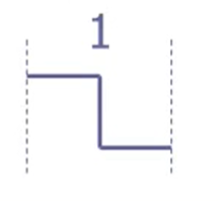
• bit中间有信号，高——低跳变为1

  

  采用曼彻斯特编码，一个时钟周期只可以表示一个bit，并且必须通过两次采样才能得到一个bit但它能携带时钟信号，且可表示没有数据传输。

• 差分曼彻斯特编码

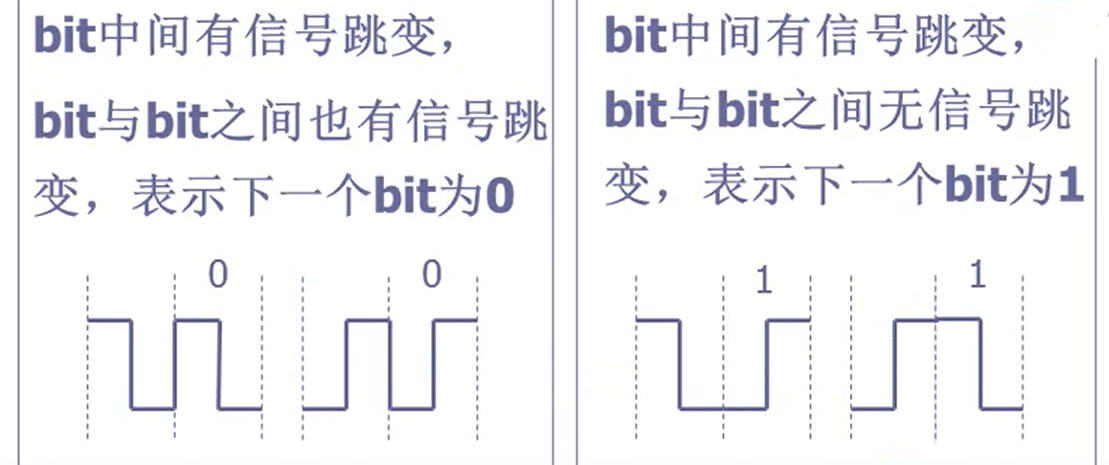
注意：每个图中都有四个bit。

差分曼彻斯特编码与曼彻斯特编码相同，但抗干扰性能强于曼彻斯特编码。

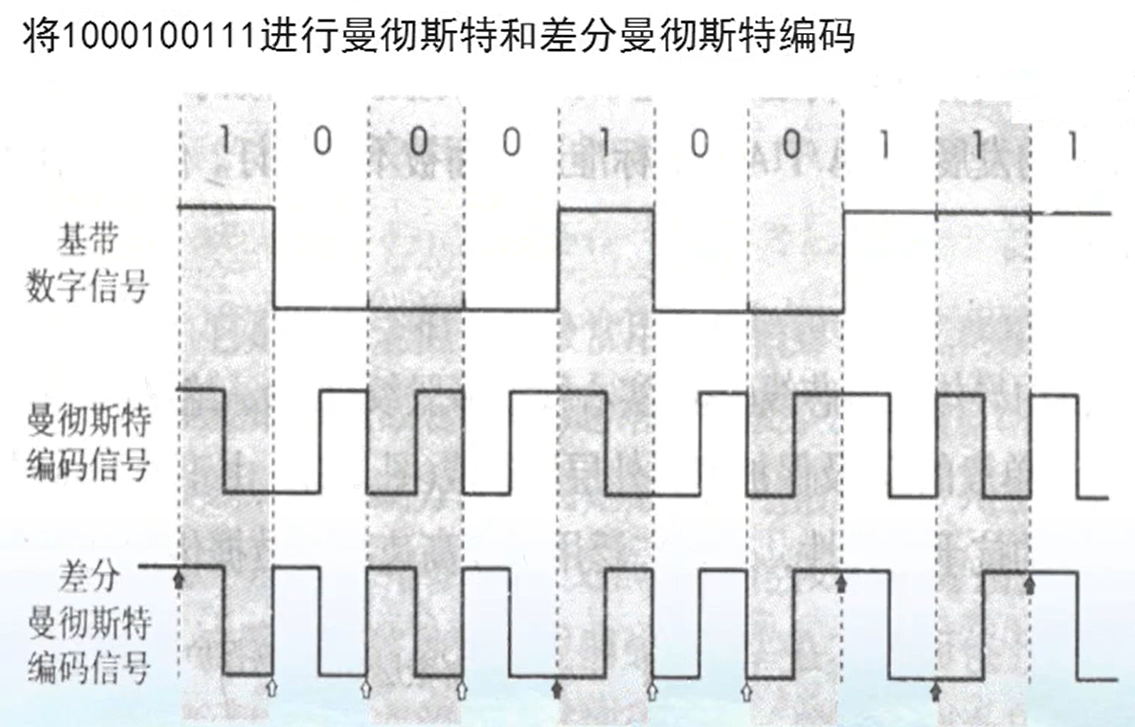
判断（差分）曼彻斯特编码时，忽略bit与bit间的“竖线”，可判断得更加清楚。

信道的极限容量

• 有失真，但可识别

  

• 失真大，无法识别

  

理想条件下的信号传输：奈氏准则

1924 年，奈奎斯特(Nyquist)就推导出了著名的奈氏准则。他给出了在假定的理想条件下，为了避免码间串扰，码元的传输速率的上限值。

在任何信道中，码元传输的速率是有上限的，否则就会出现码间串扰的问题，使接收端对码元的判决（即识别）成为不可能。（比如说话速度太快，别人就听不清你说什么了）

如果信道的频带越宽，也就是能够通过的信号高频分量越多，那么就可以用更高的速率传送码元而不出现码间串扰。

奈氏准则

理想低通信道的最高码元传输速率=2WBaud

• W是理想低通信道的带宽，单位为HZ;
• Baud是波特，是码元传输速率的单位；

波特：在调制解调器中经常用到波特这个概念，Bit是信息量，如果一个码元含有3个Bit信息量，那么1波特=3Bit/s

有干扰条件下的信号传输：香农公式

香农(Shannon)用信息论的理论推导出了带宽受限且有高斯白噪声干扰的信道的极限、无差错的信息传输速率。

式中S/N表示信噪比

• 信道的带宽或信道中的信噪比越大，则信息的极限传输速率就越高。
• 若信道带宽 W 或信噪比 S/N 没有上限（当然实际信道不可能是这样的），则信道的极限信息传输速率 C 也就没有上限。
• 实际信道上能够达到的信息传输速率要比香农的极限传输速率低不少。
  
• 对于频带宽度已确定的信道，如果信噪比不能再提高了，并且码元传输速率也达到了上限值，那么还有办法提高信息的传输速率。这就是用编码的方法让每一个码元携带更多比特的信息量。

奈氏准则和香农公式的应用范围

数据通信的基础知识

标签：数据显示   取值   时间间隔   振幅   容量   应用   距离   github   通信   

原文地址：https://www.cnblogs.com/AhuntSun-blog/p/12210579.html