标签:struct ble 复制 one line time 测试数据 一点 路径
本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步 P4779。
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
第一行包含三个整数 n,m,sn,m,s,分别表示点的个数、有向边的个数、出发点的编号。
接下来 mm 行每行包含三个整数 u,v,wu,v,w,表示一条 u \to vu→v 的,长度为 ww 的边。
输出一行 nn 个整数,第 ii 个表示 ss 到第 ii 个点的最短路径,若不能到达则输出 2^{31}-1231−1。
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
0 2 4 3
【数据范围】
对于 20\%20% 的数据:1\le n \le 51≤n≤5,1\le m \le 151≤m≤15;
对于 40\%40% 的数据:1\le n \le 1001≤n≤100,1\le m \le 10^41≤m≤104;
对于 70\%70% 的数据:1\le n \le 10001≤n≤1000,1\le m \le 10^51≤m≤105;
对于 100\%100% 的数据:1 \le n \le 10^41≤n≤104,1\le m \le 5\times 10^51≤m≤5×105,保证数据随机。
对于真正 100\%100% 的数据,请移步 P4779。请注意,该题与本题数据范围略有不同。
样例说明:
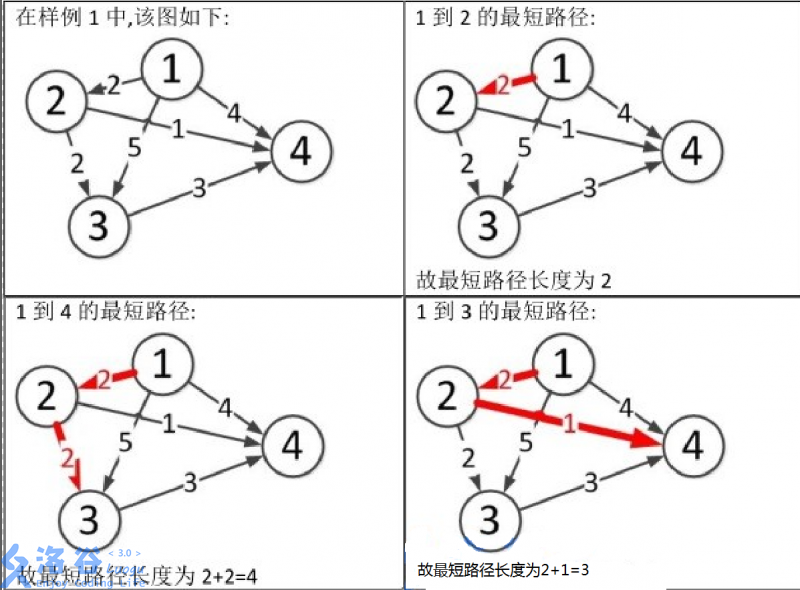
图片1到3和1到4的文字位置调换
思路
这里使用使用STL队列,首先用数组dis记录起点到每个结点的最短路径,用邻接表来存储图,用vis数组记录当前节点是否在队列中
具体操作
用队列来保存待优化的结点(类似于BFS),优化时每次取出队首结点,并且用队手节点来对最短路径进行更新并进行松弛操作
如果要对所连点的最短路径需要更新,且改点不在当前的队列中,就将改点加入队列然后不断进行松弛操作,直至队列空为止。
AC代码如下

#include<bits/stdc++.h> using namespace std; inline int read() { int x=0,k=1; char c=getchar(); while(c<‘0‘||c>‘9‘){if(c==‘-‘)k=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘)x=(x<<3)+(x<<1)+(c^48),c=getchar(); return x*k; } #define maxn 10005 #define maxm 500005 #define inf 2147483647 int n,m,s,tot,di[maxn],t[maxn]; bool vi[maxn]; struct e { int next,to,w; }h[maxm]; void add(int u,int v,int w) { h[++tot].next=t[u]; h[tot].to=v; h[tot].w=w; t[u]=tot; } queue<int> q; inline void sp() { for(int i=1; i<=n; i++) { di[i]=inf; } int u,v; q.push(s); di[s]=0; vi[s]=1; while(!q.empty()) { u=q.front(); q.pop(); vi[u]=0; for(int i=t[u];i;i=h[i].next) { v=h[i].to; if(di[v]>di[u]+h[i].w) { di[v]=di[u]+h[i].w; if(!vi[v]) { vi[v]=1; q.push(v); } } } } } int main(){ n=read(),m=read(),s=read(); for(int i=1,u,v,w;i<=m;i++) { u=read(),v=read(),w=read(); add(u,v,w); } sp(); for(int i=1; i<=n; i++) { printf("%d ",di[i]); } return 0; }
注意
这里需要注意一点,就是在原题中的一个条件“如果没有结果,则输出2^31-1”.
本人就是在这里丢掉了一个测试点的分QWQ。
标签:struct ble 复制 one line time 测试数据 一点 路径
原文地址:https://www.cnblogs.com/Michael666/p/12215710.html