梯度下降

标签：The   改变   例子   使用   最小值   无法   第一个   info   sub   

梯度下降：应用最广泛的求极小值算法。

假设一线性回归模型，它的代价函数为 J(θ₀,θ₁) 。我们的目标是最小化这个代价函数，而要得到最小的代价函数值关键就在于正确选取 θ₀和θ₁的值，于是我们引出梯度下降算法。

步骤：1. 初始化θ₀和θ₁的值，通常取0。

　　　2. 不断改变θ₀和θ₁的值，试图通过这种改变使得 J(θ₀,θ₁) 变小，直到找到 J(θ₀,θ₁) 的最小值（也可能是局部最小值）。

将上述步骤可视化

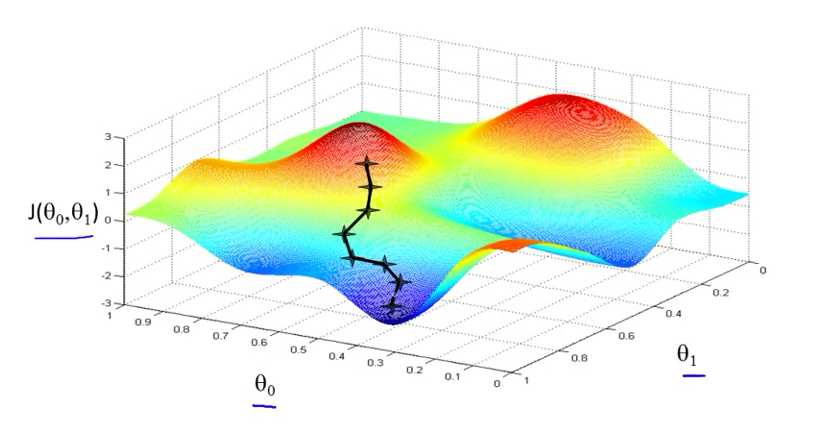
左图中，我们初始化θ₀和θ₁的值得到第一个 J(θ₀,θ₁) 点 ，在左边红色区域。假设红色区域都是一个个小山峰，我们处于第一个点的位置，现在目标是用小碎步尽快下山，环顾四周后我们可以找到下一个点，注意是下降最快的方向（坡度最陡），以此方法一直下降，知道下降到深蓝色区域里的局部最低点。

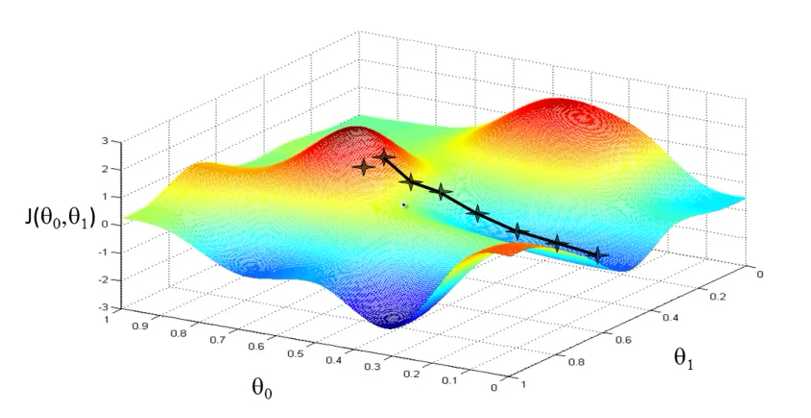
右图中亦是如此，只是θ₀和θ₁的初始值不同，导致第一个J(θ₀,θ₁) 点 不同，下降速度最快的方向也不一样，因此到达的最低点也不同。

公式

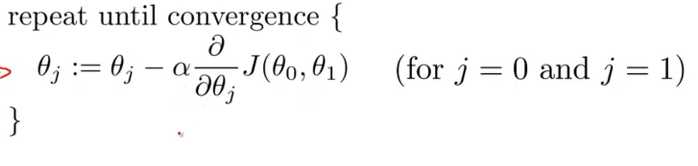
式子中，:= 符号是赋值运算符，表示把符号后面的值赋予给符号后面的值，α 表示学习率，以下山的例子就是步子的大小，α 越大，下山时步子迈得就越大，下降速度越快。

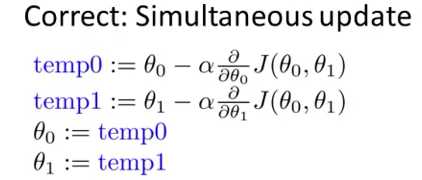
在梯度下降中，我们使用公式更新 θ₀ 和 θ₁ 的值，在更新时，我们应当同时更新 θ₀ 和 θ₁ 的值。

如果不同时更新，如上图，前一个更新后的 θ₀ 会影响到 temp1 的导数项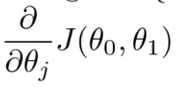，继而影响更新θ₁ 。

为了更容易理解梯度下降过程，我们假定 h_θ(x) = θ₁x, 代价函数为 J(θ₁) ，可以得到 J(θ₁) 与 θ₁ 关系图如下

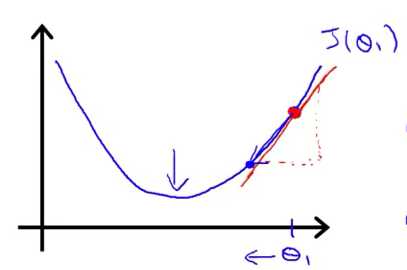
梯度下降过程即：

首先选取 θ₁ 的值，得到对应的 J(θ₁) ，标记在上图中红点位置处。现以红点作切线（上图中红色实线），此时切线的斜率即公式中的导数项，切线斜率再与学习率 α （正数）相乘  ，最后用θ₁减去它们相乘后的值，计算出的值即第一次更新后的θ₁ （向左移动），此时也可以发现对应的 J(θ₁) 位置会往左边移动，直到运动到最小值（局部最小值）。移动速度跟学习率 α 有关，如果 α 过大，每次移动也会跳跃得越大，很容易越过最小值，无法收敛，甚至发散。而事实上，在梯度下降过程中，学习率 α 会自动调整，越靠近最小值， α 会越小，移动越慢。

如果初始化 θ₁ 后，得到对应的 J(θ₁) 本身就处在最小值位置，再使用梯度下降算法， θ₁ 将不会更新，因为此时导数项为0，J(θ₁) 也不会发生变化。

梯度下降

标签：The   改变   例子   使用   最小值   无法   第一个   info   sub   

原文地址：https://www.cnblogs.com/feng-fengfeng/p/12219193.html