标签:span nlog 取出 位置 log clu 就是 scanf ++
【题目描述】
FJ打算带他的\(N(1 \leq N \leq 30,000)\)头奶牛去参加一年一度的“全美农场主大奖赛”。在这场比赛中,每个参赛者都必须让他的奶牛排成一列,然后领她们从裁判席前依次走过。 今年,竞赛委员会在接受队伍报名时,采用了一种新的登记规则:他们把所有队伍中奶牛名字的首字母取出,按它们对应奶牛在队伍中的次序排成一列(比如说,如果FJ带去的奶牛依次为Bessie、Sylvia、Dora,登记人员就把这支队伍登记为BSD)。登记结束后,组委会将所有队伍的登记名称按字典序升序排列,就得到了他们的出场顺序。 FJ最近有一大堆事情,因此他不打算在这个比赛上浪费过多的时间,也就是说,他想尽可能早地出场。于是,他打算把奶牛们预先设计好的队型重新调整一下。 FJ的调整方法是这样的:每次,他在原来队列的首端或是尾端牵出一头奶牛,把她安排到新队列的尾部,然后对剩余的奶牛队列重复以上的操作,直到所有奶牛都被插到了新的队列里。这样得到的队列,就是FJ拉去登记的最终的奶牛队列。 接下来的事情就交给你了:对于给定的奶牛们的初始位置,计算出按照FJ的调整规则所可能得到的字典序最小的队列。
【输入格式】
第1行: 一个整数:N
第2..N+1行: 第i+1行仅有1个‘A’..‘Z’中的字母,表示队列中从前往后数第i 头奶牛名字的首字母
【输出格式】
输出FJ所能得到的字典序最小的队列。每行(除了最后一行)输 出恰好80个‘A’..‘Z’中的字母,表示新队列中每头奶牛姓名的首字母。
题解
第一篇写后缀数组的题解 先放下模板代码
inline bool check(int *num, int a, int b, int l) { return num[a] == num[b] && num[a+l] == num[b+l]; }
void suffix() {
int i, j, p;
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n; i++) sum[rnk[i]=r[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i-1];
for (i = n; i >= 1; i--) sa[sum[rnk[i]]--] = i;
for (j = 1, p = 0; p <= n; j <<= 1, m = p) {
p = 0; for (i = n - j + 1; i <= n; i++) sa2[++p] = i;
for (i = 1; i <= n; i++) if (sa[i] > j) sa2[++p] = sa[i] - j;
for (i = 1; i <= n; i++) key1[i] = rnk[sa2[i]];
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n; i++) sum[key1[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i-1];
for (i = n; i >= 1; i--) sa[sum[key1[i]]--] = sa2[i];
for (swap(rnk, sa2), p = 2, rnk[sa[1]] = 1, i = 2; i <= n; i++) {
rnk[sa[i]] = check(sa2, sa[i-1], sa[i], j) ? p - 1 : p++;
}
}
}sa[i]表示字典序为第i名的后缀的起始位置 rnk[i]表示起始位置为i的后缀的排名
对这道题有什么用呢
先考虑一下暴力做法
双指针l, r记录当前已经把a[1~l-1]及a[r+1~n]的奶牛扔到新队列里,现在原队列首尾分别是牛a[l]和a[r]
若a[l]<a[r] 那么为使新队列字典序最小 显然要将a[l]先放到新队列里 反之亦然
若a[l]==a[r] 此时并不能直接判断要先把a[l]放入还是要先把a[r]放入
举个例子 样例: ACDBCB 将a[1], a[6]先后放入新队列后发现此时a[2]==a[5] 显然是要先将a[5]放入 以便下一个放a[4] 比较优
可以看出其实就是比较一下 字符串{a[2], a[3]} 和 {a[5], a[4]} 哪个字典序较小
直接比较是O(n)的 考虑如何用后缀数组优化
将a[1]~a[n]反转后接在后面 如样例: ACDBCB -> ACDBCB|BCBDCA
然后此时比较 字符串{a[2], a[3]} 和 {a[5], a[4]} 的大小就等同于比较 后缀[2~2*n]和后缀[8~2*n]的大小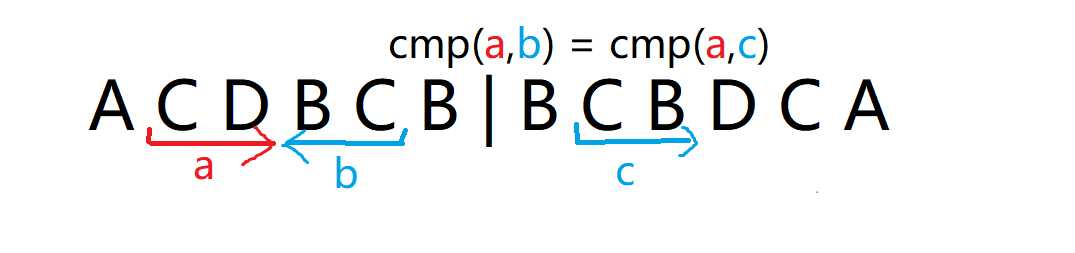
p.s. 这个技巧也经常用于处理回文串有关的问题
后缀大小排名是可以O(nlogn)预处理的 查询时就可以把r对称到另一边去 实现O(1)查询
总时间复杂度O(nlogn)
代码
#include <bits/stdc++.h>
#define mx 1000005
using namespace std;
char one_time_AC_accepted[5];
char s[mx], ans[mx];
int n, m, len;
int sa[mx], sa2[mx], rnk[mx], key[mx], sum[mx], height[mx];
inline bool check(int *num, int a, int b, int l) { return num[a] == num[b] && num[a+l] == num[b+l]; }
inline void suffix() {
int i, j, p; int *_rnk = rnk, *_sa2 = sa2, *tmp;
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= 2*n; i++) sum[_rnk[i]=s[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i-1];
for (i = 2*n; i >= 1; i--) sa[sum[_rnk[i]]--] = i;
for (j = 1; p <= 2*n; j <<= 1, m = p) {
p = 0;
for (i = n*2 - j + 1; i <= 2*n; i++) _sa2[++p] = i;
for (i = 1; i <= 2*n; i++) if (sa[i] > j) _sa2[++p] = sa[i] - j;
for (i = 1; i <= 2*n; i++) key[i] = _rnk[_sa2[i]];
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n*2; i++) sum[key[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i-1];
for (i = 2*n; i >= 1; i--) sa[sum[key[i]]--] = _sa2[i];
for (tmp = _rnk, _rnk = _sa2, _sa2 = tmp, p = 2, _rnk[sa[1]] = 1, i = 2; i <= 2*n; i++) {
_rnk[sa[i]] = check(_sa2, sa[i-1], sa[i], j) ? p - 1 : p++;
}
}
}
inline void print() {
for (int i = 1; i <= len; i++) {
putchar(ans[i]);
if (i % 80 == 0) puts("");
}
}
inline bool check(int l0, int r0) {
return rnk[(n<<1)-r0+1] > rnk[l0];
}
int main() {
scanf("%d", &n); m = 128;
for (int i = 1; i <= n; i++) {
scanf("%s", one_time_AC_accepted);
s[i] = one_time_AC_accepted[0];
}
for (int i = 1; i <= n; i++) {
s[n * 2 - i + 1] = s[i];
}
suffix();
int l = 1, r = n;
for (int i = 1; i <= n; i++) {
if (s[l] < s[r]) {
ans[++len] = s[l]; l++;
} else if (s[l] > s[r]) {
ans[++len] = s[r]; r--;
} else {
if (check(l, r)) {
ans[++len] = s[l]; l++;
} else {
ans[++len] = s[r]; r--;
}
}
}
print();
return 0;
} ```cpp
标签:span nlog 取出 位置 log clu 就是 scanf ++
原文地址:https://www.cnblogs.com/ak-dream/p/AK_DREAM27.html