标签：noi   方法   git   rri   多边形   port   imp   加速   github   

前言

1. 该篇分享来源于NFL竞赛官方的R语言版本，我做的主要是翻译为Python版本；
2. 分享中用到的技巧、构建的特征、展示数据的方式都可以应用到其他领域，比如篮球、足球、LOL、双人羽毛球等等，只要是团队竞技，都可以从中获益；
3. 分享基于kaggle上的NFL大数据碗，也就是基于橄榄球；
4. 泰森多边形的概念最好可以去了解一下，可以不用纠结于公式，看看它对一些实际问题的抽象建模表示即可；

分享目的

言简意赅的分享下在团队竞技类问题中一些有用的数据可视化、分析方法，不同的领域下对数据的处理确实千差万别，每次遇到都深感自己的不足，幸好有各位大佬们的分享，跪谢；

分享目录

1. 使用matplotlib对比赛实况进行绘制，直观理解某一时刻下的球场状态；
2. 使用泰森多边形可视化各个球员的控制区域，借以理解、量化当前的形势；
3. 结合球员们的当前位置、速度、加速度、方向等信息绘制行进路线图，可视化在N秒后的状态；
4. 分享一篇去年关于足球球员控制区域热图相关的论文中的信息，这部分没有在项目里，大家感兴趣可以看看这里；

竞赛链接

https://www.kaggle.com/c/nfl-big-data-bowl-2020

项目链接，该项目代码已经public，大家可以copy下来直接运行

https://www.kaggle.com/holoong9291/nfl-tracking-wrangling-voronoi-and-sonars-python

github仓库链接，更多做的过程中的一些思考、问题等可以在我的github中看到

https://github.com/NemoHoHaloAi/Competition/tree/master/kaggle/Top61%25-0.01404-zzz-NFL-Big-Data-Bowl

一些橄榄球相关的基本概念

• 美式足球：进攻方目的是通过跑动、传球等尽快抵达对方半场，也就是达阵，而防守方的目的则是相反，尽全力去阻止对方的前进以及尽可能断球；
• 球场长120码(109.728米），宽53码（48.768米），周长是361.992米；
• 球员：双方场上共22人，进攻方11人，防守方11人，进攻方持球；
• 进攻机会：进攻方共有四次机会，需要推进至少十码；
• 进攻方：进攻方的职责是通过四次机会，尽可能的向前推进10码或者达阵，以获得下一个四次机会，否则就需要交出球权；
• 防守方：防守方则是相反，尽可能的阻止对方前进，如果能够断球那更好，直接球权交换；
• handoff：传球；
• snap：发球；
• 橄榄球基本知识点我了解；
• QB：四分卫，通常是发球后接球的那个人，一般口袋阵的中心，但是也不乏有像拉马尔-杰克逊这样的跑传结合的QB，目前古典QB代表是新英格兰爱国者NE的汤姆-布雷迪；
• RB：跑卫，通常发球后进行冲刺、摆脱等，试图接住本方QB的传球后尽可能远的冲刺；

分享正式开始

绘制比赛实况

绘制的必要性：想象这样一种情况，我们拿到的都是比赛方的表格数据，不仅枯燥，而且不够直观，即便我们足够了解橄榄球，依然无法通过数据感受到场上紧张的氛围，进攻方的战术安排，防守方的防守计划等等，而这些实际上都是隐藏在数据中的，这就好像是玩LOL或者Dota(我个人两个都玩过，目前主要玩Dota)，我给你十个英雄的坐标、移动速度、朝向、装备，你很难理解当前的情况，但是如果看看游戏中的小地图(假设小地图能看到全部10个英雄)，我相信大部分玩家都能看出当前是在争夺肉山(抢大龙)、上高地、团战、局部团战等，因此绘制一个类似游戏中的小地图是非常有用的，会帮助我们更深刻的了解比赛；

绘制代码思路：

1. 区分进攻方和防守方，进攻方为红色，防守方为绿色（因为进攻方和防守方会交替，所以进攻方可能是球队A可能是球队B）；
2. 将持球人用黑色特别标示出来；
3. 将橄榄球场特有的码线绘制出来，这一特点在篮球和足球中是没有的，不过球队半场的概念是通用的；
4. 将得分线加粗绘制出来，得分线就是橄榄球中的TouchDown的区域，进攻方持球过了这条线得6分；

下面是相关代码：

plt.figure(figsize=(30, 15))
plt.suptitle("Sample plays, standardized, Offense moving left to right")
plt.xlabel("Distance from offensive team's own end zone")
plt.ylabel("Y coordinate")

i=1
for gp,chance in sample_chart_v2.groupby('PlayId'):
    play_id = gp
    rusher = chance[chance.NflId==chance.NflIdRusher].iloc[0]
    offense = chance[chance.IsOnOffense]
    defense = chance[~chance.IsOnOffense]
    
    plt.subplot(3,2,i)
    i+=1
    plt.xlim(0,120)
    plt.ylim(-10,63)
    
    plt.scatter(offense.X_std,offense.Y_std,marker='o',c='red',s=55,alpha=0.5,label='OFFENSE')
    plt.scatter(defense.X_std,defense.Y_std,marker='o',c='green',s=55,alpha=0.5,label='DEFENSE')
    plt.scatter([rusher.X_std],[rusher.Y_std],marker='o',c='black',s=30,label='RUSHER')
    
    for line in range(10,130,10):
        plt.plot([line,line],[-100,100],c='silver',linewidth=0.8,linestyle='-')
    
    plt.plot([rusher.YardsFromOwnGoal,rusher.YardsFromOwnGoal],[-100,100],c='black',linewidth=1.5,linestyle=':')
    plt.plot([10,10],[-100,100],c='black',linewidth=2)
    plt.plot([110,110],[-100,100],c='black',linewidth=2)
    
    plt.title(play_id)
    plt.legend()

plt.show()

下面是效果图：

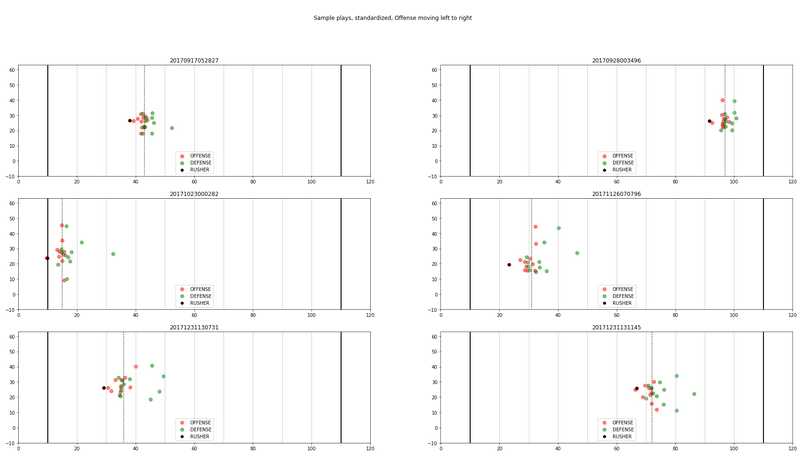
可以看到，通常对比赛实况的可视化，可以清晰的看到当前处于哪个半场，距离达阵还有多远，进攻方、防守方的站位分别是怎样，持球人周围的队友、对手数量、距离等，这非常有利于后续的分析挖掘；

绘制动态比赛实况

绘制的目的：上面的绘制能看出是静态的，而且并没有用上球员的速度、加速度、面向、移动方向等数据，而我们知道球员总是处于不断运动当中的，他们的当前状态很重要，但是1s后，2s后可能更重要，这就是这一部分绘制的目的，强调每个球员在一段时间后的状态，当然，这部分绘制有一个前提假设，那就是球员当前的速度、加速度、面向、移动方向等信息在短时间内是不变的，这一点也符合实际情况（），当然绘制与现实会有一些出入，但是这些差异不影响我们分析比赛；

绘制的代码：

plt.figure(figsize=(12, 8))
plt.suptitle("Playid:20170910001102")
plt.xlabel("Distance from offensive team's own end zone")
plt.ylabel("Y coordinate")

for gp,chance in sample_20170910001102.groupby('PlayId'):
    play_id = gp
    rusher = chance[chance.NflId==chance.NflIdRusher].iloc[0]
    offense = chance[chance.IsOnOffense]
    defense = chance[~chance.IsOnOffense]
    
    plt.subplot(1,1,1)
    i+=1
    
    x_min, x_max = chance.X_std.min()-5, chance.X_std.max()+5
    y_min, y_max = chance.Y_std.min()-5, chance.Y_std.max()+5
    plt.xlim(x_min,x_max)
    plt.ylim(y_min,y_max)
    
    plt.scatter(offense.X_std,offense.Y_std,marker='o',c='green',s=55,alpha=0.5,label='OFFENSE')
    plt.scatter(defense.X_std,defense.Y_std,marker='o',c='red',s=55,alpha=0.5,label='DEFENSE')
    plt.scatter([rusher.X_std],[rusher.Y_std],marker='o',c='black',s=30,label='RUSHER')
    
    for idx, row in chance.iterrows():
        _color='black' if row.IsBallCarrier else('green' if row.IsOnOffense else 'red')
        plt.arrow(row.X_std,row.Y_std,row.X_std_end-row.X_std,row.Y_std_end-row.Y_std,width=0.05,head_width=0.3,ec=_color,fc=_color)
    
    for line in range(10,130,10):
        plt.plot([line,line],[-100,100],c='silver',linewidth=0.8,linestyle='-')
    
    plt.plot([rusher.YardsFromOwnGoal,rusher.YardsFromOwnGoal],[-100,100],c='black',linewidth=1.5,linestyle=':')
    plt.plot([10,10],[-100,100],c='black',linewidth=2)
    plt.plot([110,110],[-100,100],c='black',linewidth=2)
    
    plt.title(play_id)
    plt.legend()

plt.show()

下面是效果图：

绘制球员的泰森多边形

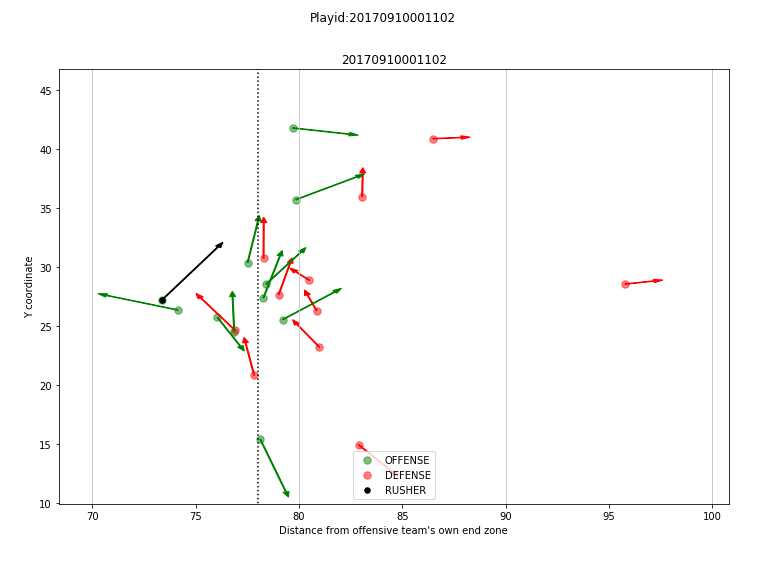
绘制的必要性：百度百科定义点泰森多边形-冯洛诺伊图，简单理解就是在一个球场中，每个球员都是一个个不重合的点，那么将整个球场划分到这些点上，那么可以认为每个点都有自己的一片控制区域，这也经常用于狮群领土划分、机场划分等问题，抽象出来都是同一个问题；

泰森多边形的局限：

1. 没有考虑球员与球员的差异；
2. 没有考虑球员的移动方向速度；
3. 没有考虑球的位置和影响；

相对来说，泰森多边形是对这一类问题的简单抽象，没有考虑一些复杂因素，但是也揭示了很多信息；

绘制代码如下：

from scipy.spatial import Voronoi

plt.figure(figsize=(12, 8))
plt.suptitle("Sample plays, standardized, Offense moving left to right")
plt.xlabel("Distance from offensive team's own end zone")
plt.ylabel("Y coordinate")

sample_20171120000963 = train_1[train_1.PlayId==20171120000963].copy()
for gp,chance in sample_20171120000963.groupby('PlayId'):
    play_id = gp
    rusher = chance[chance.NflId==chance.NflIdRusher].iloc[0]
    offense = chance[chance.IsOnOffense]
    defense = chance[~chance.IsOnOffense]
    
    plt.subplot(1,1,1)
    i+=1
    
    x_min, x_max = chance.X_std.min()-2, chance.X_std.max()+2
    y_min, y_max = chance.Y_std.min()-2, chance.Y_std.max()+2
    #plt.xlim(8,50) # 特定
    plt.xlim(x_min,x_max)
    #plt.ylim(5,40) # 特定
    plt.ylim(y_min,y_max)
    #plt.plot([x_min,x_min,x_max,x_max,x_min],[y_min,y_max,y_max,y_min,y_min],c='black',linewidth=1.5)
    
    vor = Voronoi(np.array([[row.X_std,row.Y_std] for index, row in chance.iterrows()]))
    regions, vertices = voronoi_finite_polygons_2d(vor)
    for region in regions:
        polygon = vertices[region]
        plt.plot(*zip(*polygon),c='black',alpha=0.8)
    
    plt.scatter(offense.X_std,offense.Y_std,marker='o',c='green',s=55,alpha=0.5,label='OFFENSE')
    plt.scatter(defense.X_std,defense.Y_std,marker='o',c='red',s=55,alpha=0.5,label='DEFENSE')
    plt.scatter([rusher.X_std],[rusher.Y_std],marker='o',c='black',s=30,label='RUSHER')
    
    for line in range(10,130,10):
        plt.plot([line,line],[-100,100],c='silver',linewidth=0.8,linestyle='-')
    
    plt.plot([rusher.YardsFromOwnGoal,rusher.YardsFromOwnGoal],[-100,100],c='black',linewidth=1.5,linestyle=':')
    plt.plot([10,10],[-100,100],c='black',linewidth=2)
    plt.plot([110,110],[-100,100],c='black',linewidth=2)
    
    plt.title(play_id)
    plt.legend()

plt.show()

运行效果图：

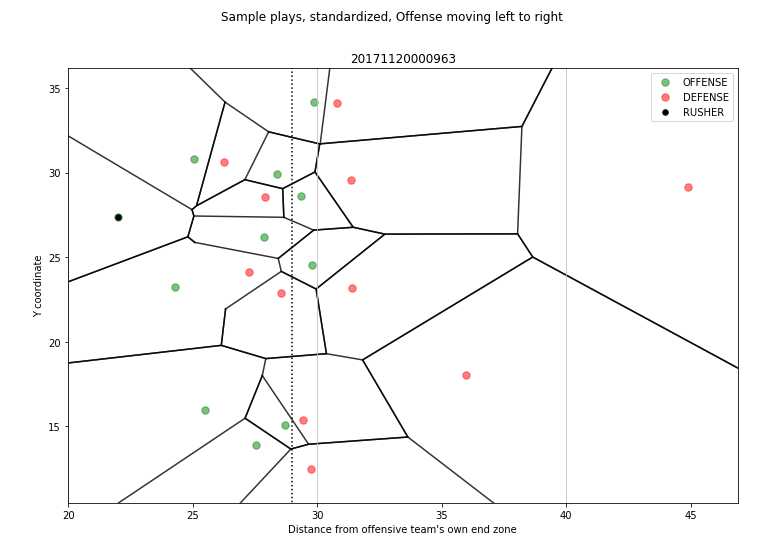
从该图中，能清晰的看到各个球员的控制区域，有一个量化因子是将这部分区域相加，量化每个球队的控制区域大小以及分布；

球员控制区域热图

这部分的分享目的：这部分分享来自这篇论文，我也还没看完，所以分享内容会比较少，简单概述一下。首先大家应该能看到泰森多边形的不足，首先它没有考虑速度等动态因素，其次它是针对每个球员而不是球队的，但是我们知道球队的信息更重要，因为这是团队竞技，因此缺乏对球员进行叠加的过程，而这些都是这篇论文重点探讨的地方；

1. 论文以足球数据为基础，量化了某个时刻的球场控制热图，且考虑了球在其中的影响，注意此时还是假设每个球员的影响在球场中都是一个圆形区域：
   
2. 但是理想状态每个球员的影响可能是圆可能是椭圆，这里我想象一个球员是一颗石子，如果垂直丢入水中（球员静置不动时），那么波纹就是一个圆形，如果是斜着抛入水中，那么波纹应该是一个与石子方向上的椭圆：
   
3. 那么引入速度、方向后的球场控制热图，就应该是下面这样：
   

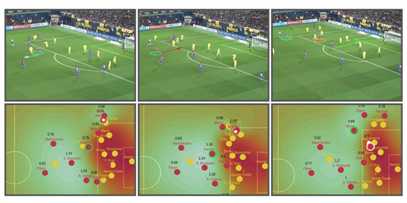
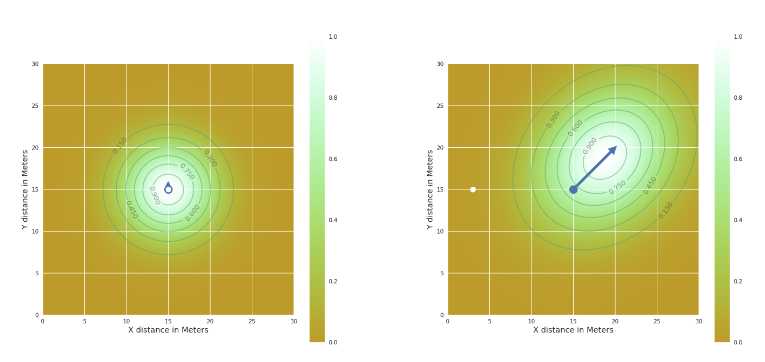
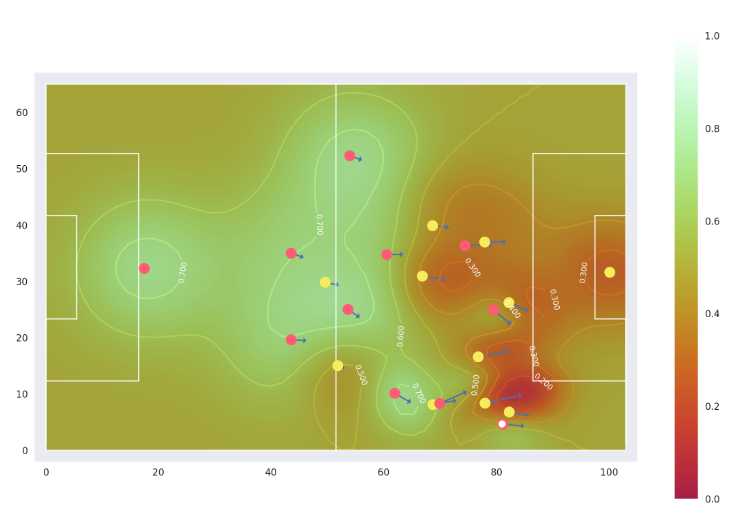
实际上这篇论文还有很多内容，且主要内容是关于如何量化球员影响区域的，也就是如何抽象为一些数学公式上，当然这部分我目前也算不上理解，所以处于外行看热闹的阶段，不过大家应该可以从中感受到数学建模的威力，以及这些东西的广泛应用，希望这篇分享能够帮到大家一点点；

最后

大家可以到我的Github上看看有没有其他需要的东西，目前主要是自己做的机器学习项目、Python各种脚本工具、数据分析挖掘项目以及Follow的大佬、Fork的项目等：
https://github.com/NemoHoHaloAi

机器学习竞赛分享：通用的团队竞技类的数据分析挖掘方法

标签：noi   方法   git   rri   多边形   port   imp   加速   github   

原文地址：https://www.cnblogs.com/helongBlog/p/12218108.html