二叉树的深度

标签：nod   image   题目   结构   turn   应该   思路   this   子节点   

题目描述

题目格式要求：

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public int TreeDepth(TreeNode root) {
        
    }
}

解题思路：

前不久刚学了动态规划，在这里“假装”用动态规划分析一下，为什么是假装呢？因为我也不知道自己是不是用的动态规划~。感觉挺像的。。。

（关于动态规划，再次推荐一下这篇文章：漫画：什么是动态规划）

动态规划有三个分析条件  ---------  最优子结构，边界，状态转移公式

1 . 首先看一下最优子结构。

对于根节点来说如果已经知道了左子树和右子树的节点，那么我们就可以得到根节点的深度是4.

再抽象一下，把2和3换成是X和Y

那么根节点的深度就应该是

（X > Y ? X : Y） + 1

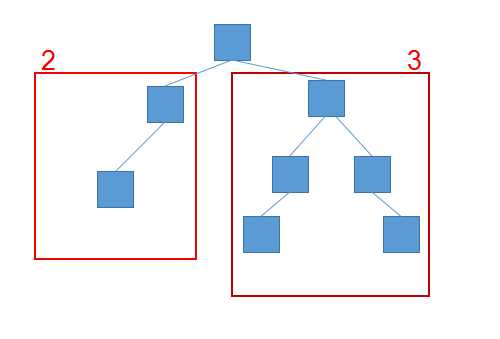
再用同样的方法去推导左子树和右子树，就可以得到相应的关系式了。

2、状态转移公式

从上面的分析不难看出状态转移公式可以写成下面这个样子。

Depth(root) =( Depth(root.left) > Depth(root.right) ?  Depth(root.left) : Depth(root.right) ) + 1

3、边界条件

a. 如果root是null，那就代表没有这个节点，返回0

b. 如果root的左右孩子节点都为空，说明这是一个叶子节点，那么它的深度就返回1

最后的代码：

public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root == null) { return 0; }
        if(root.left == null && root.right == null) { return 1; }

        int left = TreeDepth(root.left) ;
        int right = TreeDepth(root.right) ;
        return (left > right ? left : right) + 1;
    }
}

二叉树的深度

标签：nod   image   题目   结构   turn   应该   思路   this   子节点   

原文地址：https://www.cnblogs.com/cnndevelop/p/12228230.html