01层次分析法

标签：世界   完整   表示   lib   put   sorted   ros   电量   get   

1. 　　AHP（层次分析法）
2. 　　层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂（TLsaaty）正式提出。它是一种定性和定量相结合的、系统化、层次化的分析方法。由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

2. 层次分析法的基本步骤

1. 1、建立层次结构模型。在深入分析实际问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次，同一层的诸因素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用。最上层为目标层，通常只有1个因素，最下层通常为方案或对象层，中间可以有一个或几个层          次，通常为准则或指标层。当准则过多时(譬如多于9个)应进一步分解出子准则层。
2. 2、构造成对比较阵。从层次结构模型的第2层开始，对于从属于(或影响)上一层每个因素的同一层诸因素，用成对比较法和1—9比较尺度构造成对比较阵，直到最下层。
3. 3、计算权向量并做一致性检验。对于每一个成对比较阵计算最大特征根及对应特征向量，利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量(归一化后)即为权向量：若不通过，需重新构造成对比较阵。
4. 4、计算组合权向量并做组合一致性检验。计算最下层对目标的组合权向量，并根据公式做组合一致性检验，若检验通过，则可按照组合权向量表示的结果进行决策，否则需要重新考虑模型或重新构造那些一致性比率较大的成对比较阵。

2. 建立层次结构模型

1. 例--选拔干部模型
2.   　对三个干部候选人y ₁、y ₂、y ₃，按选拔干部的五个标准：品德、才能、资历、年龄和群众关系，构成如下层次分析模型：假设有三个干部候选人y ₁、y ₂、y ₃，按选拔干部的五个标准：品德，才能，资历，年龄和群众关系，构成如下层次分析模型
3. 

2. 构造成对比较矩阵

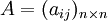1. 比较第i个元素与第j个元素相对上一层某个因素的重要性时，使用数量化的相对权重a _i j来描述。设共有n个元素参与比较，则称为成对比较矩阵。
2. 　　成对比较矩阵中a _i j的取值可参考Satty的提议，按下述标度进行赋值。a _i j在1-9及其倒数中间取值。
3. a _i j = 1，元素i与元素j对上一层次因素的重要性相同；
4. a _i j = 3，元素i比元素j略重要；
5. a _i j = 5，元素i比元素j重要；
6. a _i j = 7，元素i比元素j重要得多；
7. a _i j = 9，元素i比元素j的极其重要；
8. a _i j = 2 n，n=1,2,3,4，元素i与j的重要性介于 a _i j = 2 n − 1与 a _i j = 2 n + 1之间；
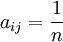9. ，n=1,2,...,9，当且仅当a _j i = n。
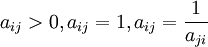10. 　　成对比较矩阵的特点：。（备注：当i=j时候，a _i j = 1）
11. 　　选拔干部考虑5个条件：品德x ₁，才能x ₂，资历x ₃，年龄x ₄，群众关系x ₅。某决策人用成对比较法，得到成对比较阵如下：
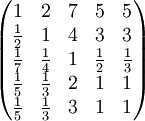12. a ₁₄ = 5表示品德与年龄重要性之比为5，即决策人认为品德比年龄重要。

2. 作一致性检验

1. 从理论上分析得到：如果A是完全一致的成对比较矩阵，应该有
2. 
3. 　　但实际上在构造成对比较矩阵时要求满足上述众多等式是不可能的。因此退而要求成对比较矩阵有一定的一致性，即可以允许成对比较矩阵存在一定程度的不一致性。
4. 　　由分析可知，对完全一致的成对比较矩阵，其绝对值最大的特征值等于该矩阵的维数。对成对比较矩阵的一致性要求，转化为要求： 的绝对值最大的特征值和该矩阵的维数相差不大。
5. 　　检验成对比较矩阵A一致性的步骤如下：
6. 计算衡量一个成对比较矩阵A （n>1 阶方阵）不一致程度的指标CI：
7. 
8. 　　RI是这样得到的:对于固定的n,随机构造成对比较阵A,其中a _i j是从1,2,…,9,1/2,1/3,…,1/9中随机抽取的.这样的A是不一致的,取充分大的子样得到A的最大特征值的平均值

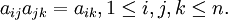
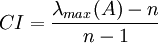
n

1

2

3

4

5

6

7

8

9

RI

0

0

0.58

0.90

1.12

1.24

1.32

1.41

1.45

注解:

从有关资料查出检验成对比较矩阵A 一致性的标准RI：RI称为平均随机一致性指标，它只与矩阵阶数n 有关（一般不超过9个）。

按下面公式计算成对比较阵A 的随机一致性比率CR：

 。

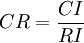判断方法如下： 当CR<0.1时，判定成对比较阵A 具有满意的一致性，或其不一致程度是可以接受的；否则就调整成对比较矩阵A，直到达到满意的一致性为止。

　　例子的矩阵

　　特征向量:  0.47439499 0.26228108 0.0544921  0.09853357 0.11029827 (相加等于1)

       算法过程 先对数组进行列相加-----  [2.04285714,3.91666667,17 ,10.5 ,10.33333333]

　　再用等到的结果除以原矩阵得到一个新的矩阵：

　　再对矩阵进行行相加等到-------[2.37197494 1.31140538 0.2724605  0.49266783 0.55149136]

　　　在进行归一化处理（上面的结果被阶数除）得到上面的特征向量（结果发现品德的影响最大）

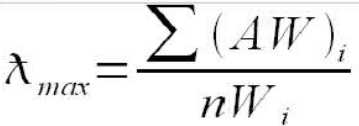
　　AW = 特征向量*原矩阵（一开始的），然后拿到每一行的和---- [2.42456102 1.34394248 0.27386595 0.50012206 0.55461416]

　　所以可得 （AW/阶数*特征向量）      5.07293180152562

　　计算得到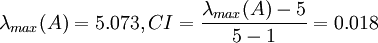,查得RI=1.12，

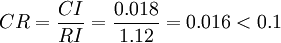
　　这说明A 不是一致阵，但A 具有满意的一致性，A 的不一致程度是可接受的。

层次总排序及决策

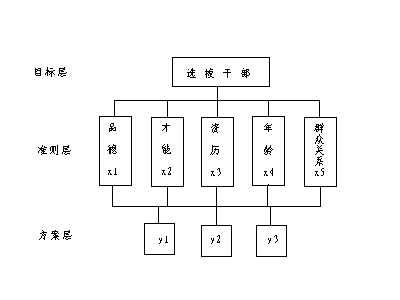
现在来完整地解决例2的问题，要从三个候选人y ₁ , y ₂ , y ₃中选一个总体上最适合上述五个条件的候选人。对此，对三个候选人y = y ₁ , y ₂ , y ₃分别比较他们的品德( x ₁ )，才能( x ₂ )，资历( x ₃ )，年龄( x ₄ )，群众关系( x ₅ )。

　　先成对比较三个候选人的品德，得成对比较阵

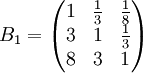
　　经计算，B ₁的权向量

ω _x 1 ( Y ) = (0.082,0.236,0.682) ^z

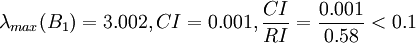
　　故B ₁的不一致程度可接受。ω _x 1 ( Y )可以直观地视为各候选人在品德方面的得分。

　　类似地，分别比较三个候选人的才能，资历，年龄，群众关系得成对比较阵

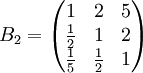
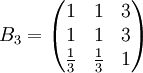
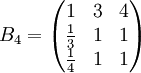         B₅₌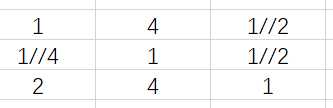

　　可得 5个特征向量

　　然后在通过

 　　　　第一个人：（0.08199023*0.47439499 (一开始的那个特征向量)+0.59488796*0.26228108 +0.42857143*0.0544921 +0.63274854*0.09853357 +0.34595035*0.11029827 ） = 总得分

　　　　后两个人类似

　最后得        第一个人得  0.31878206

　　　　　　 第二个人得 0.23919592

　　　　　　 第三个人得 0.44202202

 　　所以3号是第一候选人

层次分析法的用途举例

例如，某人准备选购一台电冰箱，他对市场上的6种不同类型的电冰箱进行了解后，在决定买那一款式时，往往不是直接拿电冰箱整体进行比较，因为存在许多不可比的因素，而是选取一些中间指标进行考察。例如电冰箱的容量、制冷级别、价格、型号、耗电量、外界信誉、售后服务等。然后再考虑各种型号冰箱在上述各中间标准下的优劣排序。借助这种排序，最终作出选购决策。在决策时，由于6种电冰箱对于每个中间标准的优劣排序一般是不一致的，因此，决策者首先要对这7个标准的重要度作一个估计，给出一种排序，然后把6种冰箱分别对每一个标准的排序权重找出来，最后把这些信息数据综合，得到针对总目标即购买电冰箱的排序权重。有了这个权重向量，决策就很容易了。

层次分析法应用的程式

　　运用AHP法进行决策时，需要经历以下4个步骤：

　　1、建立系统的递阶层次结构；

　　2、构造两两比较判断矩阵；（正互反矩阵）

　　3、针对某一个标准，计算各备选元素的权重；

　　4、计算当前一层元素关于总目标的排序权重。

　　5、进行一致性检验。

 附录 示例代码（python）

#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np RI_dict = {1: 0, 2: 0, 3: 0.58, 4: 0.90, 5: 1.12, 6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45} def get_w(array): row = array.shape[0] # 计算出阶数 a_axis_0_sum = array.sum(axis=0) # print(a_axis_0_sum) b = array / a_axis_0_sum # 新的矩阵b # print(b) b_axis_0_sum = b.sum(axis=0) b_axis_1_sum = b.sum(axis=1) # 每一行的特征向量 # print(b_axis_1_sum) w = b_axis_1_sum / row # 归一化处理(特征向量) nw = w * row AW = (w * array).sum(axis=1) # print(AW) max_max = sum(AW / (row * w)) # print(max_max) CI = (max_max - row) / (row - 1) CR = CI / RI_dict[row] if CR < 0.1: # print(round(CR, 3)) # print(‘满足一致性‘) # print(np.max(w)) # print(sorted(w,reverse=True)) # print(max_max) # print(‘特征向量:%s‘ % w) return w else: print(round(CR, 3)) print(‘不满足一致性，请进行修改‘) def main(array): if type(array) is np.ndarray: return get_w(array) else: print(‘请输入numpy对象‘) if __name__ == ‘__main__‘: # 由于地方问题，矩阵我就写成一行了 e = np.array([[1, 2, 7, 5, 5], [1 / 2, 1, 4, 3, 3], [1 / 7, 1 / 4, 1, 1 / 2, 1 / 3], [1 / 5, 1 / 3, 2, 1, 1], [1 / 5, 1 / 3, 3, 1, 1]]) a = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]]) b = np.array([[1, 2, 5], [1 / 2, 1, 2], [1 / 5, 1 / 2, 1]]) c = np.array([[1, 1, 3], [1, 1, 3], [1 / 3, 1 / 3, 1]]) d = np.array([[1, 3, 4], [1 / 3, 1, 1], [1 / 4, 1, 1]]) f = np.array([[1, 4, 1 / 2], [1 / 4, 1, 1 / 4], [2, 4, 1]]) e = main(e) a = main(a) b = main(b) c = main(c) d = main(d) f = main(f) try: res = np.array([a, b, c, d, f]) ret = (np.transpose(res) * e).sum(axis=1) print(ret) except TypeError: print(‘数据有误，可能不满足一致性，请进行修改‘)

 matlab 代码

%层次分析法（AHP） 

disp(‘请输入判断矩阵A（n阶）‘); 

A = input(‘A=‘);

01层次分析法

标签：世界   完整   表示   lib   put   sorted   ros   电量   get   

原文地址：https://www.cnblogs.com/h694879357/p/12229557.html