标签:add 题解 pac 优化 速度 put cond 代码 target
直
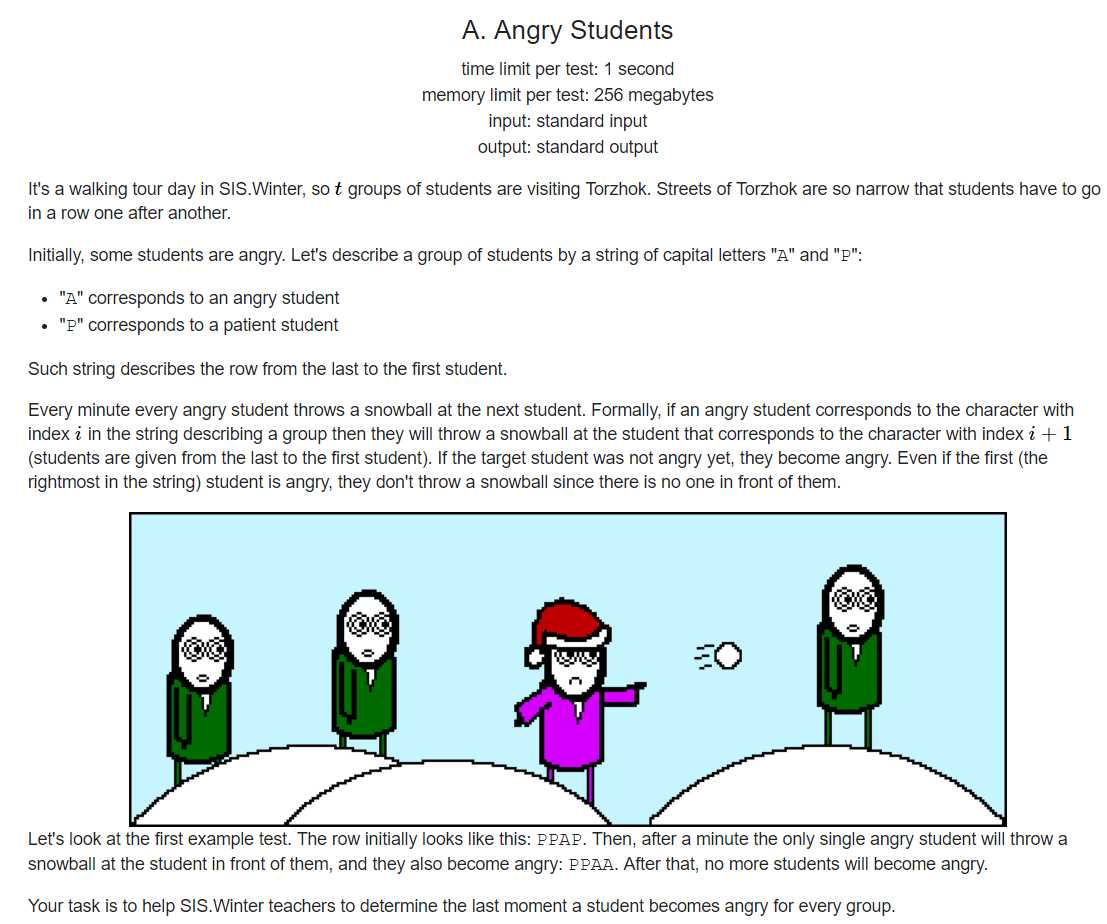
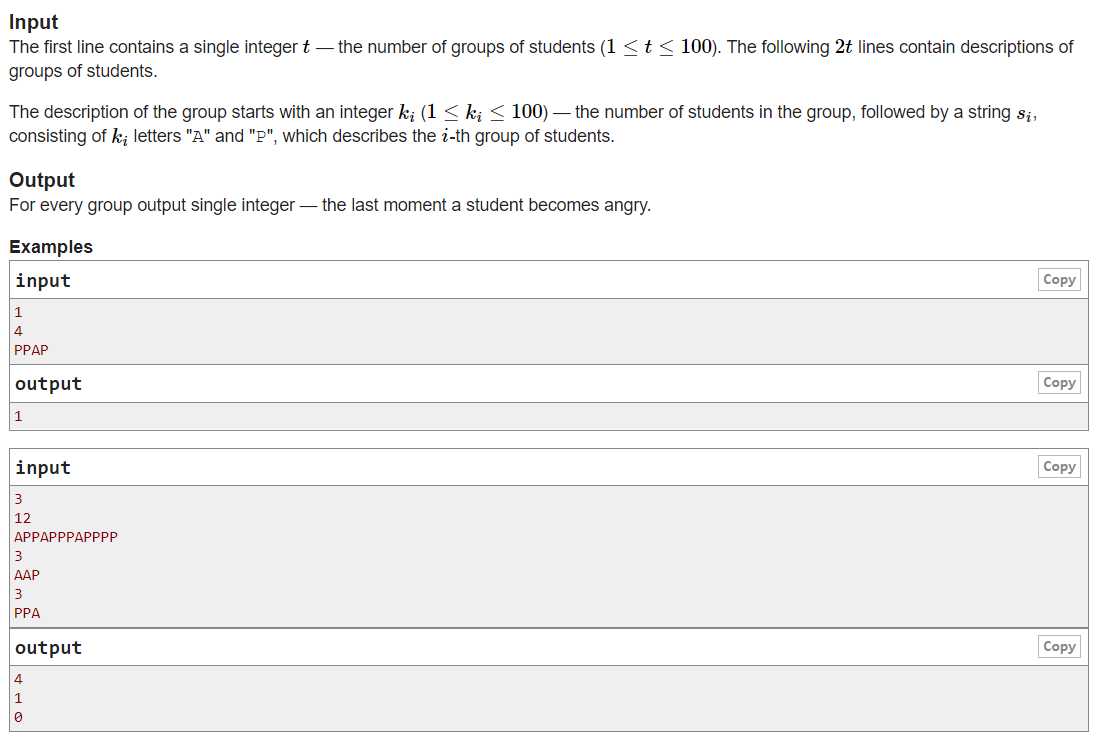
接看所有A后面连续P的个数最大值
#include<cstring>
#include<cstdio>
#include<set>
#include<iostream>
#define forn(i, n) for (int i = 0; i < int(n); i++)
#define fore(i, s, t) for (int i = s; i < (int)t; i++)
#define fi first
#define se second
using namespace std;
const int maxn=5e3+5;
const int maxm=2e5+5;
const int inf=1e9;
int main(){
int t;
cin>>t;
while(t--){
int n;
string s;
cin>>n;
cin>>s;
int ans=0;
for(int i=0;i<n;i++){
if(s[i]==‘A‘) {
int cnt=0;
while(i+cnt+1<n&&s[i+cnt+1]==‘P‘)
cnt++;
ans=max(ans,cnt);
}
}
cout<<ans<<endl;
}
}
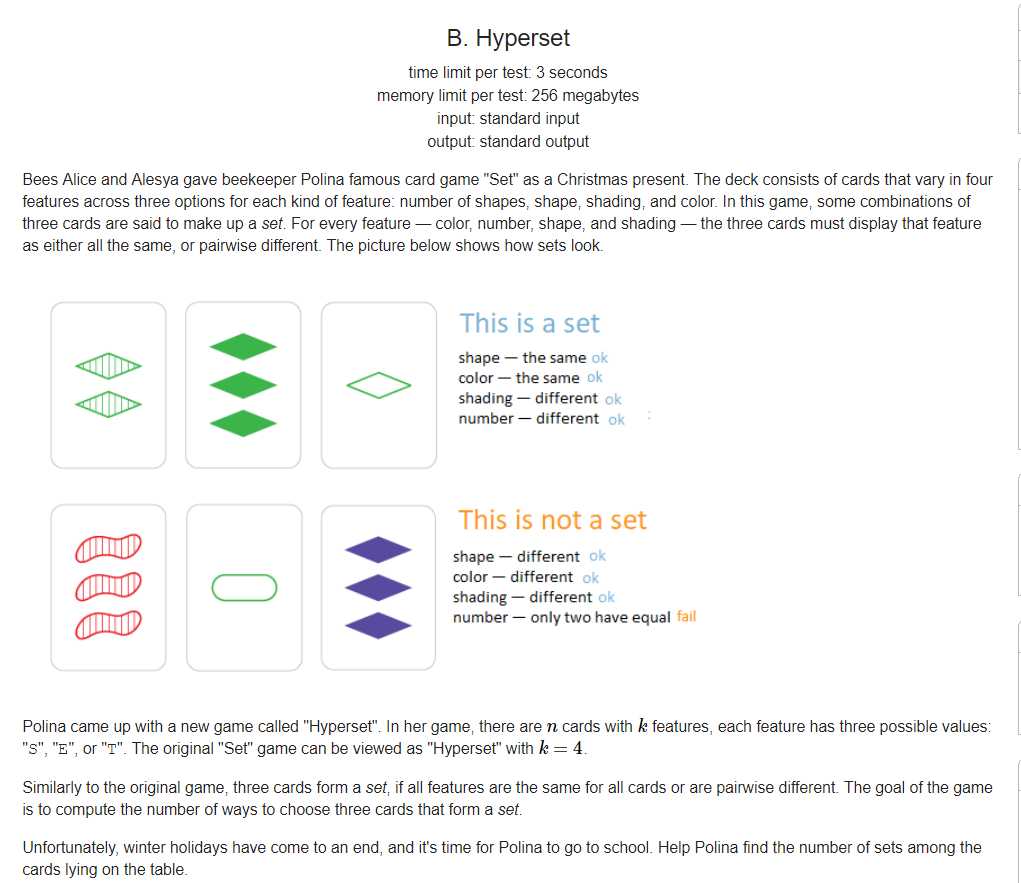
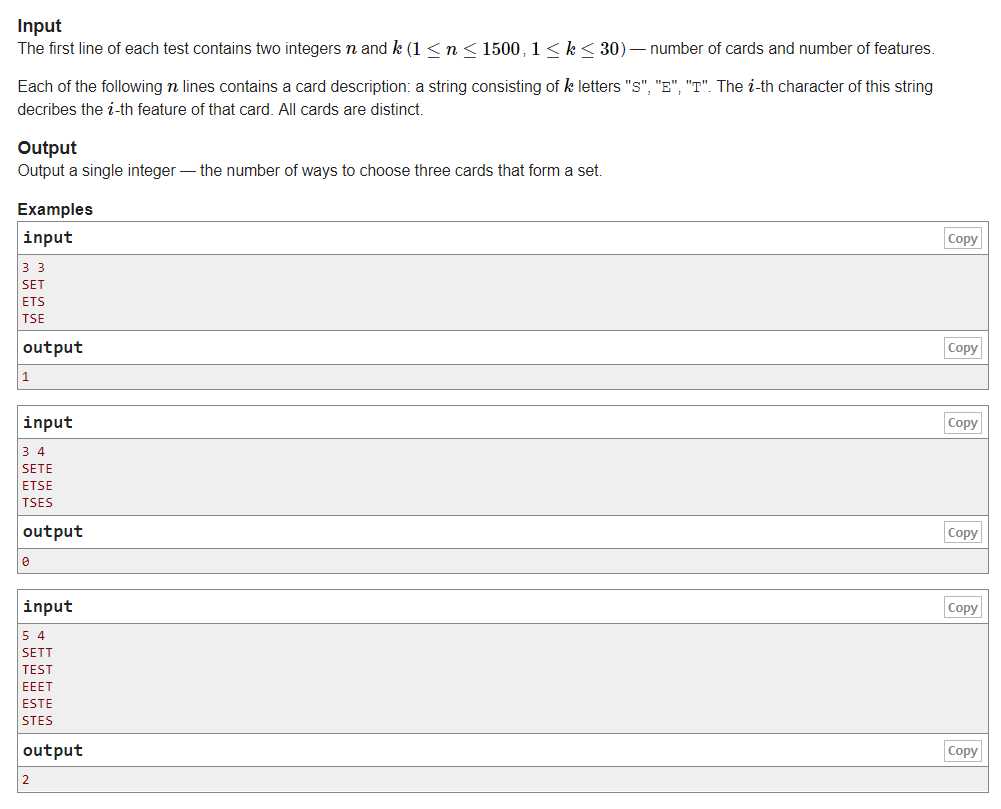
N个字符串中选择3个使得选中的3个字符串满足要么同一位置上字符相等,要么都不相同,有多少钟选法
题解:好像是个组合计数,其实就是找满足条件的三元组个数,显然可以枚举前两个然后算法第三个再去判断第三个是否存在,这样复杂度是n^2*log(n),可以过
另外写代码的时候出了个问题,

这是循环内部的代码,利用了set来找另外一个字符,但是这样写竟然是超时的,如果我们改为 if 判断的话就很快1S内跑完,而这样写3S都跑不完

按道理来讲两者速度不会差太多,但是从这里可以看出至少差了三倍以上
因此这警示我们对于循环内部的东西一定要尽量去优化他,有的东西编译器会帮我们去优化,但是谁知道哪天会出问题呢?不要留下这样一个隐患!
#include<bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
#define fore(i, s, t) for (int i = s; i < (int)t; i++)
#define fi first
#define se second
using namespace std;
const int maxn=5e3+5;
const int maxm=2e5+5;
const int inf=1e9;
int main(){
int n,m;
cin>>n>>m;
vector<string> str(n);
for(int i=0;i<n;i++)
cin>>str[i];
set<string> ls;
for(int i=0;i<n;i++)
ls.insert(str[i]);
long long ans=0;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
string target;
for(int k=0;k<m;k++){
if(str[i][k]==str[j][k]) target.push_back(str[i][k]);
else {
if(str[i][k]!=‘S‘&&str[j][k]!=‘S‘) target.push_back(‘S‘);
if(str[i][k]!=‘E‘&&str[j][k]!=‘E‘) target.push_back(‘E‘);
if(str[i][k]!=‘T‘&&str[j][k]!=‘T‘) target.push_back(‘T‘);
}
}
if(target!=str[i]&&target!=str[j]&&ls.count(target)) ans++;
}
}
cout<<ans/3<<endl;
}
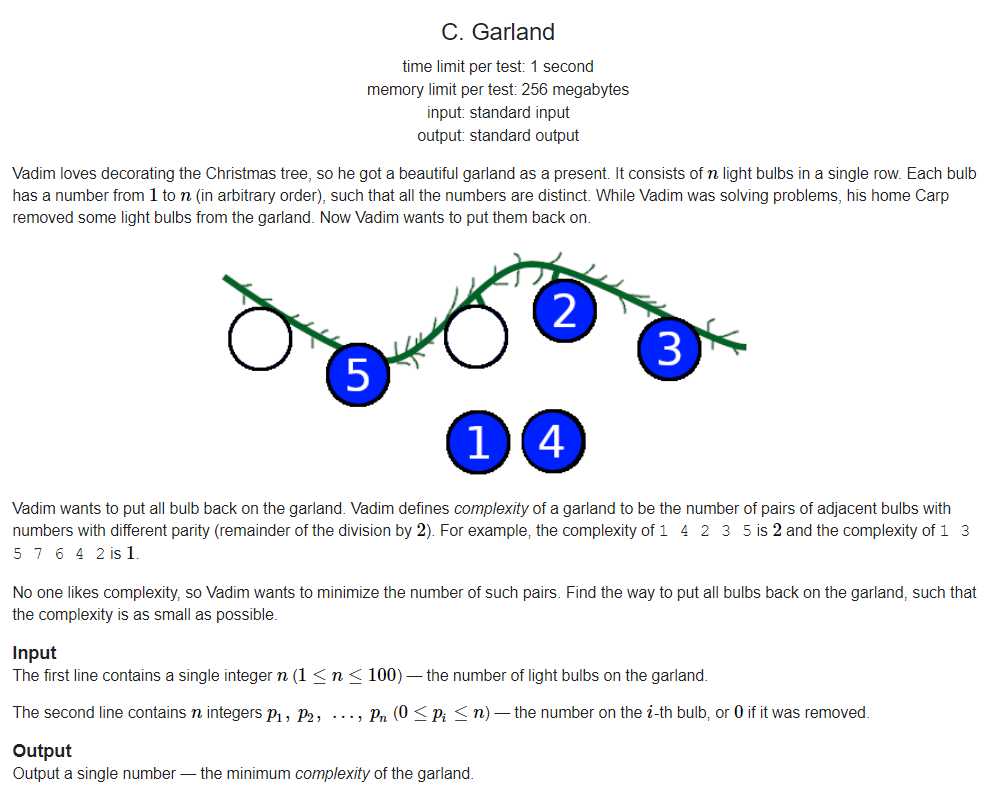

官方题解是贪心,但是显然DP可做,因此阶段性太明显了,一旦填到第i个字符,我们只需要记录已经用了多少奇数多少偶数以及现在的这个位置填哪个
因此一个四维的DP即可
#include<bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
#define fore(i, s, t) for (int i = s; i < (int)t; i++)
#define fi first
#define se second
using namespace std;
const int maxn=100+5;
const int maxm=2e5+5;
const int inf=1e9;
int n;
int pm[maxn];
int dp[maxn][maxn][maxn][2];
int main(){
cin>>n;
for(int i=1;i<=n;i++)
cin>>pm[i];
int c0=n/2,c1=(n+1)/2;
for(int i=1;i<=n;i++)
if(pm[i]) {
if(pm[i]&1) c1--;
else c0--;
}
memset(dp,0x3f,sizeof(dp));
dp[0][c0][c1][0]=dp[0][c0][c1][1]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=c0;j++){
for(int k=0;k<=c1;k++){
if(pm[i]){
if(pm[i]&1) dp[i][j][k][1]=min(dp[i-1][j][k][0]+1,dp[i-1][j][k][1]);
else dp[i][j][k][0]=min(dp[i-1][j][k][1]+1,dp[i-1][j][k][0]);
}
else {
dp[i][j][k][1]=min(dp[i-1][j][k+1][0]+1,dp[i-1][j][k+1][1]);
dp[i][j][k][0]=min(dp[i-1][j+1][k][1]+1,dp[i-1][j+1][k][0]);
}
}
}
}
cout<<min(dp[n][0][0][0],dp[n][0][0][1]);
}
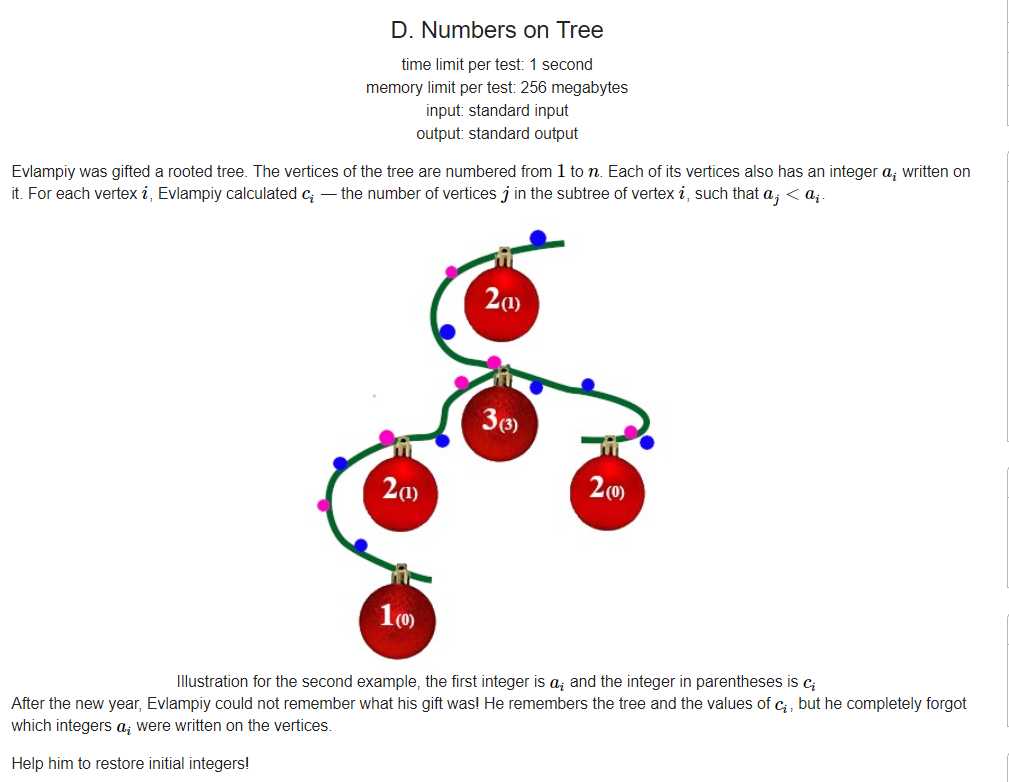
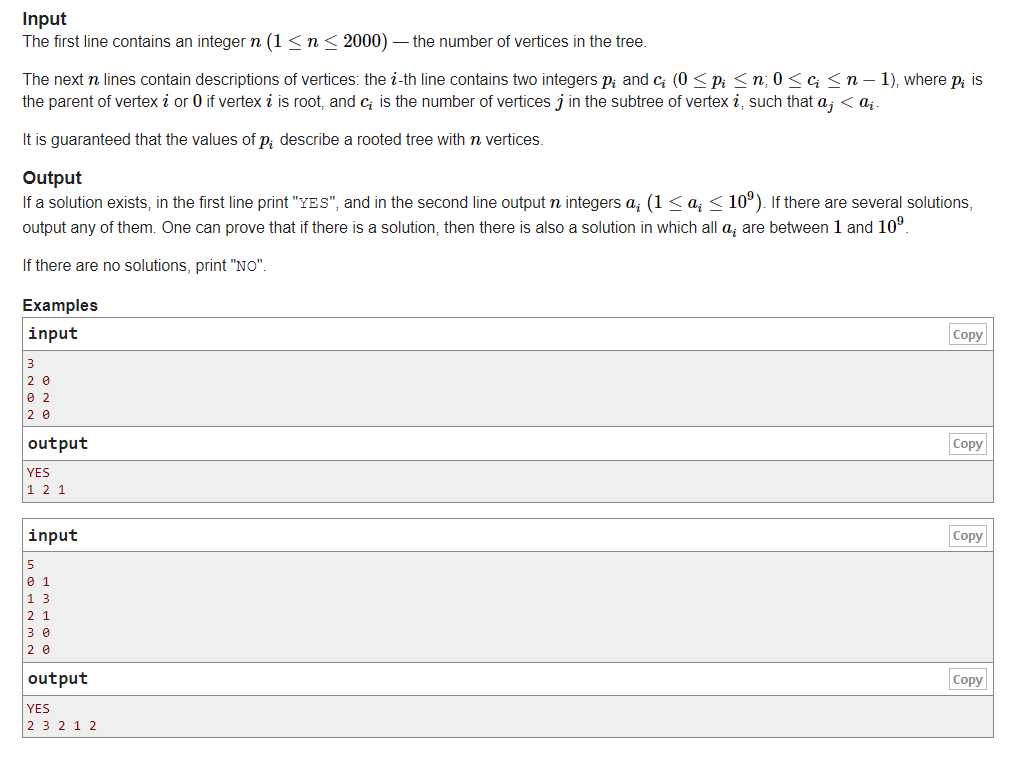
应该是这场最喜欢的一道题了,学到了很多,虽然最后懂了之后有点索然无味的感觉
首先对于我们可以在序列上考虑问题,毕竟两者相通
对于一个序列来说,我们倒序去扫描,对于最后一个数来说,假如他是3,那么我们知道他前面有3个数比他小,那么我们让给这个数赋值为4,并且把4标记一下,表示4已经被用过了
注意能这样做的前提是序列中每一个数均出现一次,并且每一个数都出现过
然后继续,如果下一个是4,那么这个数应该填的是6,因为4被用了,要比4个数大,这里只能填6了
看到这里我们就明白了,这个序列按照这样的方式一定能构造出来,除非出现数不够用的情况
然后树上的话跟序列就是一模一样的,无非是倒叙扫描变为DFS
代码的写法也可以很暴力,因为这里N<=2000,N^2的做法绝对没有问题
#include<bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
#define fore(i, s, t) for (int i = s; i < (int)t; i++)
#define fi first
#define se second
using namespace std;
const int maxn=2e3+5;
const int maxm=2e5+5;
const int inf=1e9;
int n;
int c[maxn];
int head[maxn],ver[maxn*2],nex[maxn*2],tot;
void AddEdge(int x,int y){
ver[++tot]=y,nex[tot]=head[x],head[x]=tot;
}
typedef vector<int> vi;
vi dfs(int x){
vi now;
for(int i=head[x];i;i=nex[i]){
int y=ver[i];
vi ret=dfs(y);
now.insert(now.end(),ret.begin(),ret.end());
}
if(now.size()<c[x]) {
puts("NO");exit(0);
}
now.insert(now.begin()+c[x],x);
return now;
}
int main(){
cin>>n;
int root;
for(int i=1;i<=n;i++){
int t;
cin>>t>>c[i];
if(t) AddEdge(t,i);
else root=i;
}
vi ans=dfs(root);
vector<int> a(n);
for(int i=0;i<n;i++)
a[ans[i]-1]=i+1;
puts("YES");
for(int i=0;i<n;i++)
printf("%d ",a[i]);
}
Codeforces Round #612 (Div. 2) (A-D)
标签:add 题解 pac 优化 速度 put cond 代码 target
原文地址:https://www.cnblogs.com/033000-/p/12229654.html