标签:info ret math oid 浮点 com als 方法 boolean
题目11
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
保证base和exponent不同时为0
思路
这里主要注意考虑边界条件。
1.当exponent为负数时,则是求base倒数的次方
2.当base为0时,就不能求base的负数次方,因为这样会变成求0分之一的exponent次方
3.借助公式,类似于斐波那契公式:
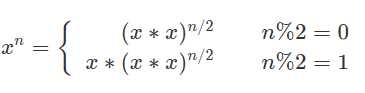
解法
public class Solution { boolean invalidInput=false; public double Power(double base, int exponent) { invalidInput=false; if(base==0.0 && exponent<0){ invalidInput=true; return 0.0; } int absExponent=exponent; if(exponent<0){ absExponent=-exponent; } double result=powerWithAbsExponent(base,absExponent); if(exponent<0){ result=1.0/result; } return result; } public double powerWithAbsExponent(double base,int exponent){ double result=1.0; for(int i=1;i<=exponent;i++){ result*=base; } return result; } }
题目
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
思路
1.注释中的解法设定两个指针,分别指向数组头尾,当遇奇偶顺序不对时,进行swap
2.但是上面的方法无法满足题目中要求的保持奇数与奇数、偶数与偶数之间的相对顺序。因此改用冒泡排序的思想,当出现前面一个数为偶数,后面一个数为奇数时,就将两个数交换。即每次遇到偶数时,就将其上浮到最右边。
解法
public class Solution { public void reOrderArray(int [] array) { /*if(array==null || array.length==0){ return; } int p1=0; int p2=array.length-1; while(p1<p2){ //若p1指向偶数 while(array[p1]%2==1){ p1++; } //若p2指向奇数 while(array[p2]%2==0){ p2--; } if(p1<p2){ int temp=array[p1]; array[p1]=array[p2]; array[p2]=temp; } }*/ for(int i=array.length-1;i>0;i--){ for(int j=0;j<i;j++){ if((array[j]%2==0) && (array[j+1]%2!=0)){ int temp=array[j]; array[j]=array[j+1]; array[j+1]=temp; } } } } }
标签:info ret math oid 浮点 com als 方法 boolean
原文地址:https://www.cnblogs.com/lyeeer/p/12222467.html