查找表

标签：算法   相等   开始   bin   while   优点   null   turn   nbsp   

基本概念：

查找表:由同一类型的数据元素（或记录）构成的集合。

关键字（键）：用来表示数据元素的数据项成为关键字，简称键，其值称为键值

主关键字：可唯一标识哥哥数据元素的关键字

查找：根据给定的某个K值，再查找表寻找一个其键值等于K的数据元素。

静态查找表：进行的是引用型运算

动态查找表：进行的是加工型运算

静态查找表：

查找表用顺序表表示：（见P163）
const int maxsize=20 //静态查找表的表长
typedef struct {
TableElem elem[maxsize+1]； /*一维数组， 0号单元留空*/
int n； /*最后一个元素的下标，也即表长*/
}SqTable ;

typedef struct {
keytype key ; /*关键字域 */
… /*其它域*/
} TableElem ;

一、过程
从表中最后一个记录开始顺序进行查找，若当前记录的
关键字=给定值，则查找成功；否则，继续查上一记录…；
若直至第一个记录尚未找到需要的记录，则查找失败。

二、算法
方法一： 使用一种设计技巧：设立岗哨
int SearchSqtable(Sqtable T, KeyType key）
{ /*在顺序表R中顺序查找其关键字等于key的元素。
若找到，则函数值为该元素在表中的位置，否则为0*/
T.elem[0].key=key;
i=T.n;
while ( T.elem[i].key!=key ) i- - ;
return i ;
}

三、算法分析
成功查找： ASL=∑ni=1Pi Ci（设每个记录的查找概率相等）
=1/n ∑ni=1（n-i+1）
=（n+1)/2
不成功查找： ASL=n+1
▲顺序查找优点：简单，对表无要求；
▲顺序查找缺点：比较次数多

1、二分查找思想：
每次找中项
.中项是，则找到；
.否则，根据此中项的关键字与给
定关键字的关系，决定在表的前
或后半部继续找。
关键点。可使下次查找范围缩小一半。
二分查找基本思想： 每次将处于查找区间中间位置
上的数据元素与给定值K比较，若不等则缩小查找区间并
在新的区间内重复上述过程，直到查找成功或查找区间长
度为0（查找不成功）为止

二分查找算法：

int SearchBin ( SqTable T, KeyType key ) {
/*在有序表R中二分查找其关键字等于K的数据元素；若找到，
则返回该元素在表中的位置， 否则返回0 */
int low,high;
low=1 ; high=T.n ;
while ( low<=high )
{ mid=(low+high)/2 ;
if (key==T.elem[mid].key) return mid;
else if (key＜ T.elem[mid].key ) high =mid-1 ;
else low=mid+1 ;
}
return (0) ;
}
分块查找

一、查找过程：
1.先建立最大（或小）关键字表——索引表（有序）
即将每块中最大（或最小）关键字及指示块首记
录在表中位置的指针依次存入一张表中，此表称为索
引表；
2.查找索引表，以确定所查元素所在块号；
将查找关键字k与索引表中每一元素（即各块中最
大关键字）进行比较，以确定所查元素所在块号；
3.在相应块中按顺序查找关键字为k的记录。

算法分析：

静态查找表的上述三种不同实现各有优缺点。其中，
顺序查找效率最低但限制最少。
二分查找效率最高，但限制最强。
而分块查找则介于上述二者之间。在实际应用中应根据需要加以选择。

算法分析：

静态查找表的上述三种不同实现各有优缺点。其中：

顺序查找效率低但限制最少

二分查找效率最高，但限制最强

而分块查找则介于上述两者之间，再实际应用中应根据需要加以选择。

一、二叉排序树
●什么是二叉排序树？
一棵二叉排序树(Binary Sort Tree)(又称二叉查找树)或者是一棵空二叉树，或者
是具有下列性质的二叉树：
① 若它的左子树不空，则左子树上所有结点的键值均小于它的根结点键值；
② 若它的右子树不空，则右子树上所有结点的键值均大于它的根结点键值；
③ 根的左、右子树也分别为二叉排序树。
●性质：
中序遍历一棵二叉排序树所得的结点访问序列是键值的递增序列。

二、二叉排序树上的查找：
1、过程：
当二叉排序树不空时，首先将给定值和根结点的关键字
比较,若相等,则查找成功；否则根据给定值与根结点关键字
间的大小关系，分别在左子树或右子树上继续进行查找。

(1)二叉排序树，对每个结点，均有：
左子树上的所有结点键值都比根的小；
右子树上的所有结点键值都比根的大。
(2)构造二叉排序树的同时也对序列排序了。

BinTree SearchBST(BinTree bst ,KeyType key)
/*在根指针bst所指的二叉排序树上递归地查找键值等于key的结点。若成功，则返回指
向该结点的指针，否则返回空指针*/

else if ( key<bst->key)
return SearchBST (bst->lchild, key); //继续在左子树中查找
else
return SearchBST (bst->rchild, key); //继续在右子树中查找
}
由上面的查找过程可知：在二叉排序树上进行查找， 若查找成功，则是从根结点出发走
了一条从根结点到待查结点的路径；若查找不成功，则是从根结点出发走了一条从根到
某个叶子的路径。因此与二分查找类似，关键字比较的次数不超过二叉树的深度

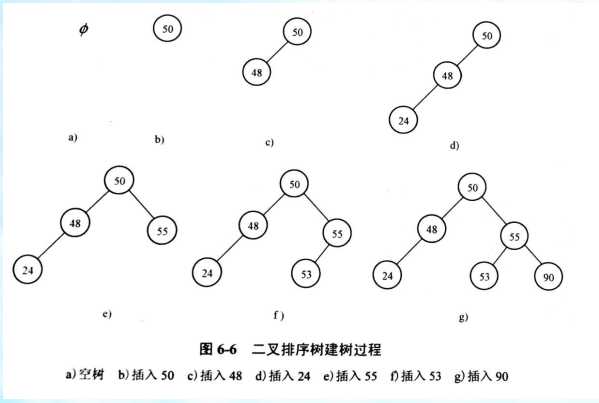
二叉排序树的插入和生成★
对序列R={k1， k2， …， kn}， k1～ kn均为关键字值，则
按下列原则可构造二叉排序树：
(1)令k1为根；
(2)若k1＜k2 ，则令k2为k1的右孩，否则为左孩；
(3) k3， k4， …， kn递归重复（2）

 ◆散列函数（哈希函数） ——设记录表A，长为n， ai
（1≤i≤n）为表中某一元素， ki为其关键字，则关键
字ki和元素ai在表中的地址之间有一函数关系，即：
Addr（ai） = H（ki）

◆散列地址——由散列函数决定数据元素的存储位置，该位置
称为散列地址。

冲突：

k1≠ k2 但 H（k1） =H（k2）的现象称为冲突。
即：不同的关键字映射到同一存储单元。
并称k1和k2是同义词。

常用散列

1、数字分析法

2、除留余数法

3.平方取中法

4.基数转换法

查找表

标签：算法   相等   开始   bin   while   优点   null   turn   nbsp   

原文地址：https://www.cnblogs.com/X404/p/12230838.html