标签:个数 view 目标 new 节点数据 存储 img 表数 链式存储结构
将具有“一对一”关系的数据“线性”地存储到物理空间中,这种存储结构就称为线性存储结构(简称线性表)。数据存储的成功与否,取决于是否能将数据完整地复原成它本来的样子。对于线性表,不管是集中存放(顺序存储)还是分散存放(链式存储),数据的位置依旧没有发生改变。
使用线性表存储的数据,要求数据类型必须一致。
将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构(简称顺序表)。数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构(简称链表)。对于具有“一对一”逻辑关系的数据,在线性表中:
某一元素的左侧相邻元素称为“直接前驱”,位于此元素左侧的所有元素都统称为“前驱元素”;某一元素的右侧相邻元素称为“直接后继”,位于此元素右侧的所有元素都统称为“后继元素”。
顺序表存储数据时,会提前申请一整块足够大小的物理空间,然后将数据依次存储起来,存储时做到数据元素之间不留一丝缝隙。
使用顺序表存储数据之前,除了要申请足够大小的物理空间之外,为了方便后期使用表中的数据,顺序表还需要实时记录以下 2 项数据:顺序表申请的存储容量;顺序表的长度,也就是表中存储数据元素的个数。正常状态下,顺序表申请的存储容量要大于顺序表的长度。
1 typedef struct Table{
2 int * head; //声明了一个名为head的长度不确定的数组,也叫“动态数组”
3 int length; //记录当前顺序表的长度
4 int size; //记录顺序表分配的存储容量
5 }table;
6
7 //注意:head 是我们声明的一个未初始化的动态数组,不要只把它看做是普通的指针。
需要做如下工作:
给 head 动态数据申请足够大小的物理空间;
给 size 和 length 赋初值。
1 #define Size 5 //对Size进行宏定义,表示顺序表申请空间的大小
2 table initTable(){
3 table t;
4 //构造一个空的顺序表,动态申请存储空间
5 t.head=(int*)malloc(Size*sizeof(int));
6 if (!t.head)
7 {
8 //如果申请失败,作出提示并直接退出程序
9 printf("初始化失败");
10 exit(0);
11 }
12 t.length=0; //空表的长度初始化为0
13 t.size=Size; //空表的初始存储空间为Size
14 return t;
15 }
整个顺序表初始化的过程被封装到了一个函数中,此函数返回值是一个已经初始化完成的顺序表。好处是增加了代码的可用性,也更加美观。顺序表初始化过程中,要注意对物理空间的申请进行判断,对申请失败的情况进行处理。
此时通过在主函数中调用 initTable 语句,就可以成功创建一个空的顺序表。可向表中添加元素:
1 //向顺序表中添加元素
2 for (int i=1; i<=Size; i++) {
3 t.head[i-1]=i;
4 t.length++;
5 }
可以输出结果即说明创建顺序表成功。
向已有顺序表中插入数据元素,根据插入位置的不同,可分为以下 3 种情况:
①插入到顺序表的表头;②在表的中间位置插入元素;③尾随顺序表中已有元素,作为顺序表中的最后一个元素。
数据元素插入顺序表中的位置有所不同,但是都使用的是同一种方式去解决,即:通过遍历,找到数据元素要插入的位置,然后做如下两步工作:①将要插入位置元素以及后续的元素整体向后移动一个位置;②将元素放到腾出来的位置上;

1 //插入函数,其中,elem为插入的元素,add为插入到顺序表的位置
2 table addTable(table t,int elem,int add)
3 {
4 //判断插入本身是否存在问题(如果插入元素位置比整张表的长度+1还大(如果相等,是尾随的情况),或者插入的位置本身不存在,程序作为提示并自动退出)
5 if (add>t.length+1||add<1) {
6 printf("插入位置有问题\n");
7 return t;
8 }
9 //做插入操作时,首先需要看顺序表是否有多余的存储空间提供给插入的元素,如果没有,需要申请
10 if (t.length==t.size) {
11 t.head=(int *)realloc(t.head, (t.size+1)*sizeof(int));
12 if (!t.head) {
13 printf("存储分配失败\n");
14 return t;
15 }
16 t.size+=1;
17 }
18 //插入操作,需要将从插入位置开始的后续元素,逐个后移
19 for (int i=t.length-1; i>=add-1; i--) {
20 t.head[i+1]=t.head[i];
21 }
22 //后移完成后,直接将所需插入元素,添加到顺序表的相应位置
23 t.head[add-1]=elem;
24 //由于添加了元素,所以长度+1
25 t.length++;
26 return t;
27 }
注意:动态数组额外申请更多物理空间使用的是 realloc 函数。并且,在实现后续元素整体后移的过程,目标位置其实是有数据的,还是 3,只是下一步新插入元素时会把旧元素直接覆盖。
只需找到目标元素,并将其后续所有元素整体前移 1 个位置即可,这样实现将目标元素间接删除。
1 //删除操作
2 for (int i=add; i<t.length; i++) {
3 t.head[i-1]=t.head[i];
4 }
5 t.length--;
顺序表中查找目标元素,可以使用多种查找算法实现。顺序查找算法查找如下:
1 for (int i=0; i<t.length; i++) {
2 if (t.head[i]==elem) {
3 return i+1;
4 }
5 }
更改元素的实现过程是:找到目标元素;直接修改该元素的值。
1 //顺序查找算法查找到元素位置
2 //由于返回的是元素在顺序表中的位置,所以-1就是该元素在数组中的下标
3 t.head[add-1]=newElem;
4 return t;
链表,别名链式存储结构或单链表,用于存储逻辑关系为 "一对一" 的数据。与顺序表不同,链表不限制数据的物理存储状态,换句话说,使用链表存储的数据元素,其物理存储位置是随机的。为了体现出各数据之间的逻辑关系,链表的解决方案是,每个数据元素在存储时都配备一个指针,用于指向自己的直接后继元素。数据元素随机存储,并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。
链表中每个数据的存储都由以下两部分组成:数据元素本身,其所在的区域称为数据域;指向直接后继元素的指针,所在的区域称为指针域。链表中每个节点的具体实现:
1 typedef struct Link{
2 char elem; //代表数据域
3 struct Link * next; //代表指针域,指向直接后继元素
4 }link;
5 //link为节点名,每个节点都是一个 link 结构体
一个完整的链表需要由以下几部分构成:
头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据;
节点:链表中的节点又细分为头节点、首元节点和其他节点:
头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题;
首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,没有实际意义;
其他节点:链表中其他的节点;
注意:链表中有头节点时,头指针指向头节点;反之,若链表中没有头节点,则头指针指向首元节点。
创建一个链表需要做如下工作:声明一个头指针(如果有必要,可以声明一个头节点);创建多个存储数据的节点,在创建的过程中,要随时与其前驱节点建立逻辑关系。创建一个存储 {1,2,3,4} 且无头节点的链表:
创建头指针和首元节点;初始化首元节点;循环创建其他节点。

1 link * initLink(){
2 link * p=NULL; //创建头指针
3 link * temp = (link*)malloc(sizeof(link)); //创建首元节点
4 //首元节点先初始化
5 temp->elem = 1;
6 temp->next = NULL;
7 p = temp; //头指针指向首元节点
8 //从第二个节点开始创建
9 for (int i=2; i<5; i++) {
10 //创建一个新节点并初始化
11 link *a=(link*)malloc(sizeof(link));
12 a->elem=i;
13 a->next=NULL;
14 //将temp节点与新建立的a节点建立逻辑关系
15 temp->next=a;
16 //指针temp每次都指向新链表的最后一个节点,其实就是 a节点,这里写temp=a也对
17 temp=temp->next;
18 }
19 //返回建立的节点,只返回头指针 p即可,通过头指针即可找到整个链表
20 return p;
21 }
创建一个存储 {1,2,3,4} 且含头节点的链表:

1 link * initLink(){
2 link * p=(link*)malloc(sizeof(link)); //创建一个头结点
3 link * temp=p; //声明一个指针指向头结点
4 //生成链表
5 for (int i=1; i<5; i++) {
6 link *a=(link*)malloc(sizeof(link));
7 a->elem=i;
8 a->next=NULL;
9 temp->next=a;
10 temp=temp->next;
11 }
12 return p;
13 }
注意:若使用带有头节点创建链表的方式,输出链表时判断指针指向的结点的next不是NULL,就输出数据。
同顺序表一样,向链表中增添元素,根据添加位置不同,可分为以下 3 种情况:①插入到链表的头部(头节点之后),作为首元节点;②插入到链表中间的某个位置;③插入到链表的最末端,作为链表中最后一个数据元素。
只需以下两步操作,即可将新元素插入到指定的位置:①将新结点的 next 指针指向插入位置后的结点;②将插入位置前结点的 next 指针指向插入结点。注意:链表插入元素的操作必须是先步骤 ①,再步骤 ②;反之,若先执行步骤 ②,除非再添加一个指针,作为插入位置后续链表的头指针,否则会导致插入位置后的这部分链表丢失,无法再实现步骤 ①。

1 //p为原链表,elem表示新数据元素,add表示新元素要插入的位置
2 link * insertElem(link * p, int elem, int add) {
3 link * temp = p; //创建临时结点temp
4 //首先找到要插入位置的上一个结点
5 for (int i = 1; i < add; i++) {
6 temp = temp->next;
7 if (temp == NULL) {
8 printf("插入位置无效\n");
9 return p;
10 }
11 }
12 //创建插入结点c
13 link * c = (link*)malloc(sizeof(link));
14 c->elem = elem;
15 //向链表中插入结点
16 c->next = temp->next;
17 temp->next = c;
18 return p;
19 }
插入的步骤:
①创建临时结点temp;②找到要插入位置的上一个结点;③创建插入结点;④向链表中插入结点。
从链表中删除数据元素需要进行以下 2 步操作:①将结点从链表中摘下来;②手动释放掉结点,回收被结点占用的存储空间。
实现①只需找到要删除节点的直接前驱节点 temp,执行
1 temp->next=temp->next->next;
即可。

1 //p为原链表,add为要删除元素的值
2 link * delElem(link * p, int add) {
3 link * temp = p;
4 //遍历到被删除结点的上一个结点
5 for (int i = 1; i < add; i++) {
6 temp = temp->next;
7 if (temp->next == NULL) {
8 printf("没有该结点\n");
9 return p;
10 }
11 }
12 //单独设置一个指针指向被删除结点,以防丢失
13 link * del = temp->next;
14 //删除某个结点的方法就是更改前一个结点的指针域
15 temp->next = temp->next->next;
16 free(del); //手动释放该结点,防止内存泄漏
17 return p;
18 }
在链表中查找指定数据元素,最常用的方法是:从表头依次遍历表中节点,用被查找元素与各节点数据域中存储的数据元素进行比对,直至比对成功或遍历至链表最末端的 NULL。

1 //p为原链表,elem表示被查找元素、
2 int selectElem(link * p,int elem){
3 //新建一个指针t,初始化为头指针 p
4 link * t=p;
5 int i=1;
6 //由于头节点的存在,因此while中的判断为t->next
7 while (t->next) {
8 t=t->next;
9 if (t->elem==elem) {
10 return i;
11 }
12 i++;
13 }
14 //程序执行至此处,表示查找失败
15 return -1;
16 }
更新链表中的元素,只需通过遍历找到存储此元素的节点,对节点中的数据域做更改操作即可。

1 //更新函数,其中,add 表示更改结点在链表中的位置,newElem 为新的数据域的值
2 link *amendElem(link * p,int add,int newElem){
3 link * temp=p;
4 temp=temp->next; //在遍历之前,temp指向首元结点
5 //遍历到待更新结点
6 for (int i=1; i<add; i++) {
7 temp=temp->next;
8 }
9 temp->elem=newElem;
10 return p;
11 }
也是线性存储结构的一种,它兼顾了顺序表和链表的优点于一身。使用静态链表存储数据,数据全部存储在数组中(和顺序表一样),但存储位置是随机的,数据之间"一对一"的逻辑关系通过一个整形变量(称为"游标",和指针功能类似)维持(和链表类似)。通常,静态链表会将第一个数据元素放到数组下标为 1 的位置(a[1])中。通过 "数组+游标" 的方式存储具有线性关系数据的存储结构就是静态链表。
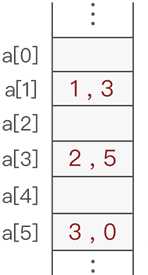
从 a[1] 存储的数据元素 1 开始,通过存储的游标变量 3,就可以在 a[3] 中找到元素 1 的直接后继元素 2;同样,通过元素 a[3] 存储的游标变量 5,可以在 a[5] 中找到元素 2 的直接后继元素 3,这样的循环过程直到某元素的游标变量为 0 截止(因为 a[0] 默认不存储数据元素)。
静态链表存储数据元素也需要自定义数据类型,至少需要包含以下 2 部分信息:①数据域:用于存储数据元素的值;②游标:其实就是数组下标,表示直接后继元素所在数组中的位置。可设计为:
1 typedef struct {
2 int data; //数据域
3 int cur; //游标
4 }component;
静态链表中,除了数据本身通过游标组成的链表外,还需要有一条连接各个空闲位置的链表,称为备用链表。备用链表的作用是回收数组中未使用或之前使用过(目前未使用)的存储空间,留待后期使用。也就是说,静态链表使用数组申请的物理空间中,存有两个链表,一条连接数据,另一条连接数组中未使用的空间。
通常,备用链表的表头位于数组下标为 0(a[0]) 的位置,而数据链表的表头位于数组下标为 1(a[1])的位置。静态链表中设置备用链表的好处是,可以清楚地知道数组中是否有空闲位置,以便数据链表添加新数据时使用。若静态链表中数组下标为 0 的位置上存有数据,则证明数组已满。
大致步骤如下:
①在数据链表未初始化之前,数组中所有位置都处于空闲状态,因此都应被链接在备用链表上;

1 //将结构体数组中所有分量链接到备用链表中
2 void reserveArr(component *array){
3 for (int i=0; i<maxSize; i++) {
4 array[i].cur=i+1;//将每个数组分量链接到一起
5 array[i].data=-1;
6 }
7 array[maxSize-1].cur=0;//链表最后一个结点的游标值为0
8 }
备用链表摘除节点最简单的方法是摘除 a[0] 的直接后继节点;同样,向备用链表中添加空闲节点也是添加作为 a[0] 新的直接后继节点。

1 //从备用链表上摘下空闲节点的函数
2 int mallocArr(component * array){
3 //若备用链表非空,则返回分配的结点下标,否则返回 0(当分配最后一个结点时,该结点的游标值为 0)
4 int i=array[0].cur;
5 if (array[0].cur) {
6 array[0].cur=array[i].cur;
7 }
8 return i;
9 }
②当向静态链表中添加数据时,需提前从备用链表中摘除节点,以供新数据使用;
③循环②,直至游标为0。

1 //初始化静态链表
2 int initArr(component *array){
3 reserveArr(array);
4 int body=mallocArr(array);
5 //声明一个变量,把它当指针使,指向链表的最后的一个结点,因为链表为空,所以和头结点重合
6 int tempBody=body;
7 for (int i=1; i<4; i++) {
8 int j=mallocArr(array);//从备用链表中拿出空闲的分量
9 array[tempBody].cur=j;//将申请的空闲分量链接在链表的最后一个结点后面
10 array[j].data=i;//给新申请的分量的数据域初始化
11 tempBody=j;//将指向链表最后一个结点的指针后移
12 }
13 array[tempBody].cur=0;//新的链表最后一个结点的指针设置为0
14 return body;
15 }
实现过程:
①从备用链表中摘除一个节点,用于存储元素 ;
②找到添加位置的前一个节点,将该节点的游标赋值给新元素 ;
③将新元素所在数组中的下标赋值给添加位置的前一个节点的游标。

1 //向链表中插入数据,body表示链表的头结点在数组中的位置,add表示插入元素的位置,a表示要插入的数据
2 void insertArr(component * array,int body,int add,char a){
3 int tempBody=body; //tempBody做遍历结构体数组使用
4 //找到要插入位置的上一个结点在数组中的位置
5 for (int i=1; i<add; i++) {
6 tempBody=array[tempBody].cur;
7 }
8 int insert=mallocArr(array); //申请空间,准备插入
9 array[insert].data=a;
10 //新插入结点的游标等于其直接前驱结点的游标
11 array[insert].cur=array[tempBody].cur;
12 //直接前驱结点的游标等于新插入结点所在数组中的下标
13 array[tempBody].cur=insert;
14 }
静态链表中删除指定元素,只需实现以下 2 步操作:①将存有目标元素的节点从数据链表中摘除;②将摘除节点添加到备用链表,以便下次再用。

1 //备用链表回收空间的函数,其中array为存储数据的数组,k表示未使用节点所在数组的下标
2 void freeArr(component * array,int k){
3 array[k].cur=array[0].cur;
4 array[0].cur=k;
5 }
6 //删除结点函数,a 表示被删除结点中数据域存放的数据
7 void deletArr(component * array,int body,char a){
8 int tempBody=body;
9 //找到被删除结点的位置
10 while (array[tempBody].data!=a) {
11 tempBody=array[tempBody].cur;
12 //当tempBody为0时,表示链表遍历结束,说明链表中没有存储该数据的结点
13 if (tempBody==0) {
14 printf("链表中没有此数据");
15 return;
16 }
17 }
18 //运行到此,证明有该结点
19 int del=tempBody;
20 tempBody=body;
21 //找到该结点的上一个结点,做删除操作
22 while (array[tempBody].cur!=del) {
23 tempBody=array[tempBody].cur;
24 }
25 //将被删除结点的游标直接给被删除结点的上一个结点
26 array[tempBody].cur=array[del].cur;
27 //回收被摘除节点的空间
28 freeArr(array, del);
29 }
只能通过逐个遍历静态链表的方式,查找存有指定数据元素的节点。

1 //在以body作为头结点的链表中查找数据域为elem的结点在数组中的位置
2 int selectElem(component * array,int body,char elem){
3 int tempBody=body;
4 //当游标值为0时,表示链表结束
5 while (array[tempBody].cur!=0) {
6 if (array[tempBody].data==elem) {
7 return tempBody;
8 }
9 tempBody=array[tempBody].cur;
10 }
11 return -1;//返回-1,表示在链表中没有找到该元素
12 }
只需找到目标元素所在的节点,直接更改节点中的数据域即可。

1 //在以body作为头结点的链表中将数据域为oldElem的结点,数据域改为newElem
2 void amendElem(component * array,int body,char oldElem,char newElem){
3 int add=selectElem(array, body, oldElem);
4 if (add==-1) {
5 printf("无更改元素");
6 return;
7 }
8 array[add].data=newElem;
9 }
双向,指的是各节点之间的逻辑关系是双向的,但通常头指针只设置一个,除非实际情况需要。双向链表中各节点包含以下 3 部分信息:①指针域:用于指向当前节点的直接前驱节点;②数据域:用于存储数据元素。③指针域:用于指向当前节点的直接后继节点。
1 typedef struct line{
2 struct line * prior; //指向直接前趋
3 int data;
4 struct line * next; //指向直接后继
5 }line;
需要注意的是:与单链表不同,双链表创建过程中,每创建一个新节点,都要与其前驱节点建立两次联系,分别是:①将新节点的 prior 指针指向直接前驱节点;②将直接前驱节点的 next 指针指向新节点。

1 line* initLine(line * head){
2 //创建链表第一个结点(首元结点)
3 head=(line*)malloc(sizeof(line));
4 head->prior=NULL;
5 head->next=NULL;
6 head->data=1;
7 line * list=head;
8 for (int i=2; i<=3; i++) {
9 //创建并初始化一个新结点
10 line * body=(line*)malloc(sizeof(line));
11 body->prior=NULL;
12 body->next=NULL;
13 body->data=i;
14
15 list->next=body; //直接前趋结点的next指针指向新结点
16 body->prior=list; //新结点指向直接前趋结点
17 list=list->next;
18 }
19 return head;
20 }
根据数据添加到双向链表中的位置不同,可细分为以下 3 种情况:①表头;②中间位置;③表尾。
第一种情况:
将新数据元素添加到表头,只需要将该元素与表头元素建立双层逻辑关系即可。假设新元素节点为 temp,表头节点为 head,则需要做以下 2 步操作即可:①temp->next=head; head->prior=temp;②将 head 移至 temp,重新指向新的表头。
第二种情况:
双向链表中间位置添加数据需要经过以下 2 个步骤:①新节点先与其直接后继节点建立双层逻辑关系;②新节点的直接前驱节点与之建立双层逻辑关系。
第三种情况:
与添加到表头是一个道理,实现过程如下:①找到双链表中最后一个节点;②让新节点与最后一个节点进行双层逻辑关系。

1 line * insertLine(line * head,int data,int add){
2 //新建数据域为data的结点
3 line * temp=(line*)malloc(sizeof(line));
4 temp->data=data;
5 temp->prior=NULL;
6 temp->next=NULL;
7 //插入到链表头,要特殊考虑
8 if (add==1) {
9 temp->next=head;
10 head->prior=temp;
11 head=temp;
12 }else{
13 line * body=head;
14 //找到要插入位置的前一个结点
15 for (int i=1; i<add-1; i++) {
16 body=body->next;
17 }
18 //判断条件为真,说明插入位置为链表尾
19 if (body->next==NULL) {
20 body->next=temp;
21 temp->prior=body;
22 }else{
23 body->next->prior=temp;
24 temp->next=body->next;
25 body->next=temp;
26 temp->prior=body;
27 }
28 }
29 return head;
30 }
双链表删除结点时,只需遍历链表找到要删除的结点,然后将该节点从表中摘除即可。

1 //删除结点的函数,data为要删除结点的数据域的值
2 line * delLine(line * head,int data){
3 line * temp=head;
4 //遍历链表
5 while (temp) {
6 //判断当前结点中数据域和data是否相等,若相等,摘除该结点
7 if (temp->data==data) {
8 temp->prior->next=temp->next;
9 temp->next->prior=temp->prior;
10 free(temp);
11 return head;
12 }
13 temp=temp->next;
14 }
15 printf("链表中无该数据元素");
16 return head;
17 }
从表头依次遍历表中元素。

1 //head为原双链表,elem表示被查找元素
2 int selectElem(line * head,int elem){
3 //新建一个指针t,初始化为头指针 head
4 line * t=head;
5 int i=1;
6 while (t) {
7 if (t->data==elem) {
8 return i;
9 }
10 i++;
11 t=t->next;
12 }
13 //程序执行至此处,表示查找失败
14 return -1;
15 }
更改双链表中指定结点数据域的操作是在查找的基础上完成的。实现过程是:通过遍历找到存储有该数据元素的结点,直接更改其数据域即可。

1 //更新函数,其中,add 表示更改结点在双链表中的位置,newElem 为新数据的值
2 line *amendElem(line * p,int add,int newElem){
3 line * temp=p;
4 //遍历到被删除结点
5 for (int i=1; i<add; i++) {
6 temp=temp->next;
7 }
8 temp->data=newElem;
9 return p;
10 }
实现约瑟夫环,如下:
定义链表结构:

1 typedef struct node{
2 int number;
3 struct node * next;
4 }person;
初始化链表:

1 person * initLink(int n){
2 person * head=(person*)malloc(sizeof(person));
3 head->number=1;
4 head->next=NULL;
5 person * cyclic=head;
6 for (int i=2; i<=n; i++) {
7 person * body=(person*)malloc(sizeof(person));
8 body->number=i;
9 body->next=NULL;
10 cyclic->next=body;
11 cyclic=cyclic->next;
12 }
13 cyclic->next=head; //首尾相连
14 return head;
15 }
主要功能实现:

1 void findAndKillK(person * head,int k,int m){
2 person * tail=head;
3 //找到链表第一个结点的上一个结点,为删除操作做准备
4 while (tail->next!=head) {
5 tail=tail->next;
6 }
7 person * p=head;
8 //找到编号为k的人
9 while (p->number!=k) {
10 tail=p;
11 p=p->next;
12 }
13 //从编号为k的人开始,只有符合p->next==p时,说明链表中除了p结点,所有编号都出列了,
14 while (p->next!=p) {
15 //找到从p报数1开始,报m的人,并且还要知道数m-1de人的位置tail,方便做删除操作。
16 for (int i=1; i<m; i++) {
17 tail=p;
18 p=p->next;
19 }
20 tail->next=p->next;//从链表上将p结点摘下来
21 printf("出列人的编号为:%d\n",p->number);
22 free(p);
23 p=tail->next;//继续使用p指针指向出列编号的下一个编号,游戏继续
24 }
25 printf("出列人的编号为:%d\n",p->number);
26 free(p);
27 }
循环链表和动态链表唯一不同在于它的首尾连接,这也注定了在使用循环链表时,附带最多的操作就是遍历链表。在遍历的过程中,尤其要注意循环链表虽然首尾相连,但并不表示该链表没有第一个节点和最后一个结点。所以,不要随意改变头指针的指向。
标签:个数 view 目标 new 节点数据 存储 img 表数 链式存储结构
原文地址:https://www.cnblogs.com/Sheenagh/p/12230836.html