标签:mamicode __name__ span strong 大学 for png ota src
以前小的时候学习图形变换采用的是比较笨的方法,如图形对直线采用对称变换,先要算出各个点到直线的垂线长度,然后做对称,一个个的点算一遍。但是在计算机图形学中采用了线性代数的方法,基于齐次坐标、矢量运算等,学完我简直震惊了,实在是太有用了!
一些小先修:
1. 齐次坐标:用n+1维的向量表示一个n维向量,可用矩阵运算来实现坐标变换,也可以表示无穷远的点(第n维为0)
2. 各种变换方法,但得注意的是这些变换都得基于标准形式,如旋转是关于原点旋转,以下PPT截图来自北京化工大学李辉老师



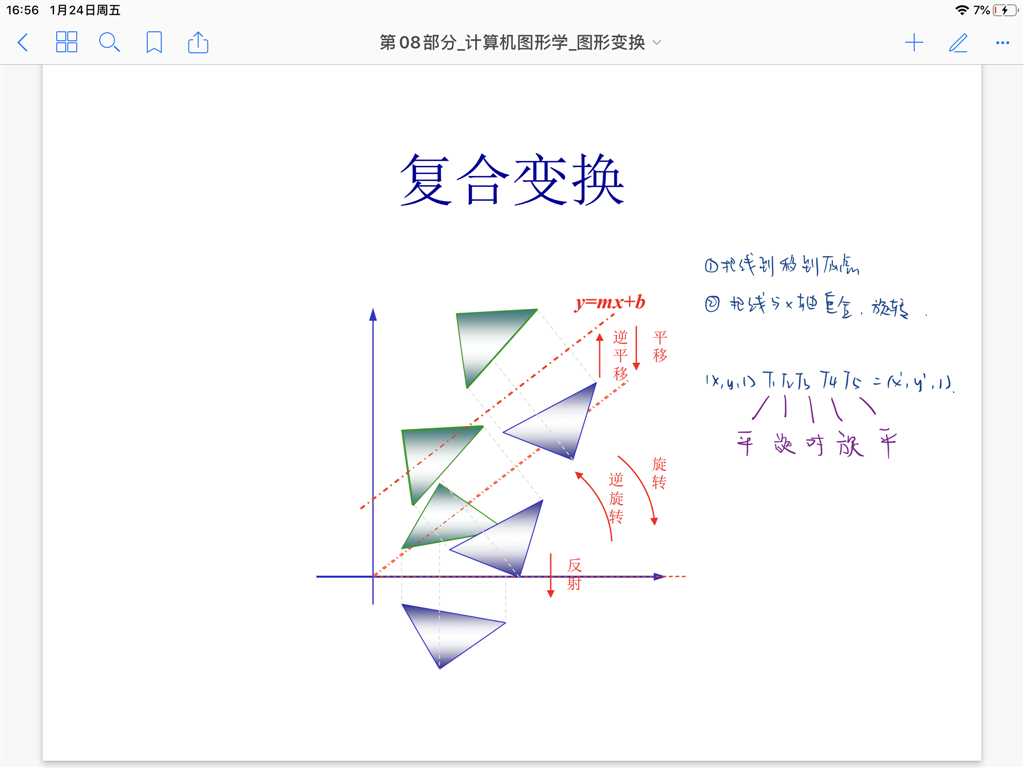
3. 对于如下的变换:三角形关于直线对称
可以将它分解为复合变换的形式,1??将直线的起点平移至原点 2??将直线旋转至与x轴正半轴重合 3??三角形关于x轴正半轴对称 4??将直线旋转回去 5??将直线平移回去
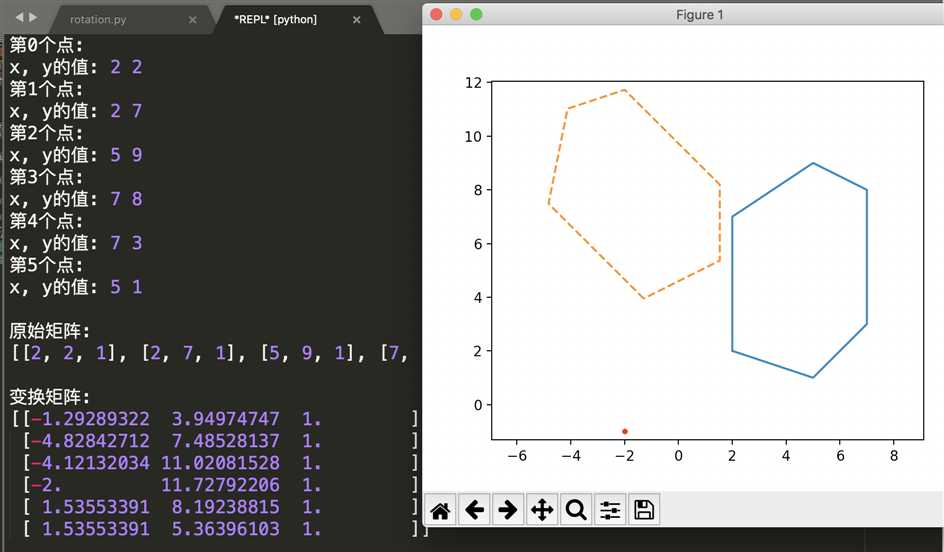
实现代码: 六边形关于P(-2,-1)旋转45度
import matplotlib.pyplot as plt import numpy from numpy import * import numpy as np import math #六边形 num = 6
def rotation(polygon): #将P(-2,-1)移到原点,平移矩阵 P1 = array([ [1, 0, 0], [0, 1, 0], [2, 1, 1]]) #绕原点旋转45度,sin(45)=con(45)=0.707106781 T = array([ [0.707106781, 0.707106781, 0], [-0.707106781, 0.707106781, 0], [0, 0, 1]]) #旋转之后再平移回去 P2 = array([ [1, 0, 0], [0, 1, 0], [-2, -1, 1]]) #做矩阵乘法 res = np.dot(polygon, np.dot(np.dot(P1, T), P2)) x = [] y = [] for i in range(num): x.append(res[i][0]) y.append(res[i][1]) x.append(res[0][0]) y.append(res[0][1]) plt.plot(x, y, ‘--‘) print("\n变换矩阵:") print(res) if __name__ == ‘__main__‘: #构造多边形 polygon = [] for i in range(num): polygon.append([]) state = "第"+str(i)+"个点: " print(state) polygon[i] = [int(n) for n in input(‘x, y的值: ‘).split()] polygon[i].append(1) print("\n原始矩阵:") print(polygon) x = [] y = [] for i in range(num): x.append(polygon[i][0]) y.append(polygon[i][1]) x.append(polygon[0][0]) y.append(polygon[0][1]) plt.plot(x, y) rotation(polygon) plt.plot(-2, -1,‘r.‘) plt.axis("equal") plt.show()
运行截图:
标签:mamicode __name__ span strong 大学 for png ota src
原文地址:https://www.cnblogs.com/swenw/p/12232370.html