标签:如何 rop 红色 width gradient ima 参数 http oca
1. 前向传播和反向传播
①前向传播 forward propagation:从前往后,根据输入和参数计算输出值和损失值,并将当地梯度(local gradient),即每个结点的输出值对该节点的输入值的偏导数,保留
在内存中以供反向传播计算梯度时使用,注意:前一个结点的输出是后一个结点的输入
②反向传播 back propagation:从后往前,利用链式求导法则,计算损失函数值对各参数 / 输入值 / 中间值的偏导数 / 梯度,梯度下降法需要使用反向传播来计算梯度
在利用梯度下降法对权重矩阵等参数进行训练/更新时,需要利用反向传播去计算损失函数对权重参数的偏导数


2. 反向传播的过程:
△正向传播时,在计算流程图中,每一个结点计算并保存该节点的输出值对输入值的偏导数 / 导数,即局部梯度(local gradient)
①将输出值和标签代入损失函数,计算出损失值。损失值作为第一个数值参与计算,记为S,开始计算导数 / 偏导,S对S求导=1,所以从后面开始第一个为1
②每遇到一个节点,根据链式求导法则,将已经计算过的上游梯度(从后面过来已经计算过的梯度)乘于局部梯度,即可得到损失函数值对该参数的梯度。从整体上看,是遇到
结点一直累乘下去。
③有几类需要特别注意的计算:
(1)结点的运算为 * 时:局部梯度=另一个元素(二元)/ 其他元素的乘积(多元)
(2)结点运算为 + 时:局部梯度为1(因为只对自己求导)
(3)结点运算为 max 时:max的数(最大的数)的梯度为其本身,其他数的梯度为0(因为只选择了最大的数,其他的数对于结果并没有影响)

④当向量作为输入时,如何计算梯度:当变量是向量时,梯度的形状与向量的形状相同(绿色的是输入值、输出值,红色的是梯度)
最后一个结点的函数是L2,导数是2q_i * x_j,又x_j =1,所以经过L2后,梯度变为2;然后向量【0.22,0.26】乘以上游梯度2,得【0.44,0.52】;又到上一个顶点 * ,注意:
这里的x的局部梯度不是W,W的局部梯度也不是x,因为W和x是向量,不是数值,不可以直接这么计算。这里设q = W * x,得矩阵,如图所示。在对计算结果(矩阵)的各元
素求偏导,即可得到当地梯度。上游梯度 * 当地梯度就可以啦!


链式求导:

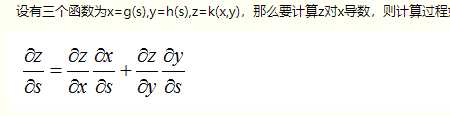
梯度与本地梯度的关系:
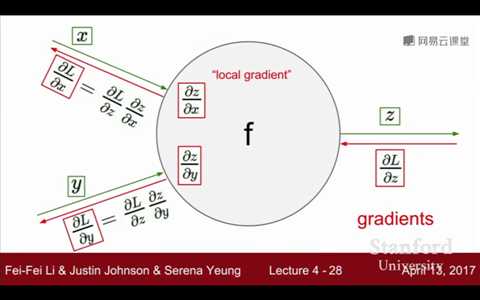
3. 例子






4. forward、backward代码

标签:如何 rop 红色 width gradient ima 参数 http oca
原文地址:https://www.cnblogs.com/shiliuxinya/p/12232440.html